Giải bài tập SGK Toán 7 Bài 4: Tính chất ba đường trung tuyến của tam giác

Cho \(G\) là trọng tâm của tam giác \(DEF\) với đường trung tuyến \(DH\). Trong các khẳng định sau đây, khẳng định nào đúng?

\(\dfrac{DG}{DH}= \dfrac{1}{2}\); \(\dfrac{DG}{GH}= 3\) 

\(\dfrac{GH}{DH}= \dfrac{1}{3}\); \(\dfrac{GH}{DG}= \dfrac{2}{3}\)

Hướng dẫn giải

\(G\) là trọng tâm của tam giác \(DEF\) với đường trung tuyến \(DH\). Ta có:

\(\dfrac{{DG}}{{DH}} = \dfrac{2}{3}\) nên ta gọi \(DG = 2a;DH = 3a\left( {a > 0} \right)\)

Suy ra \(GH=DH-DG=3a-2a=a\)

Từ đó ta có: 

\(\begin{array}{l}
\dfrac{{DG}}{{GH}} = \dfrac{{2a}}{a} = 2;\dfrac{{GH}}{{DH}} = \dfrac{a}{{3a}} = \dfrac{1}{3};\\
\dfrac{{GH}}{{DG}} = \dfrac{a}{{2a}} = \dfrac{1}{2}
\end{array}\)

Vậy khẳng định \(\dfrac{GH}{DH}= \dfrac{1}{3}\) là đúng.

Các khẳng định còn lại sai.

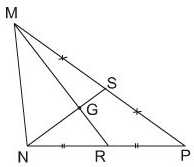
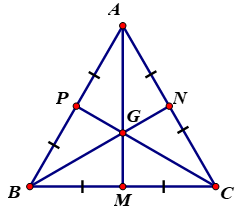
Cho hình \(25\). Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau:

a)  \(MG = … MR ;\) \(GR = … MR ;\) \(GR = … MG\)

b)  \(NS = ... NG;\) \(NS = …GS;\) \(NG = ... GS\)

Hướng dẫn giải

Từ hình vẽ ta thấy: \(S, R\) lần lượt là trung điểm của \(MP;\,NP\) nên \(NS\) và \(MR\) là hai đường trung tuyến của tam giác \(MNP\).

\(G\) là giao của hai đường trung tuyến nên \(G\) là trọng tâm của \(ΔMNP\), do đó ta có thể điền như sau:

Câu a:

\(MG =\dfrac{2}{3} MR ;\) \(GR = \dfrac{1}{3} MR ;\) \(GR =\dfrac{1}{2} MG.\)

Vì \(G\) là trọng tâm của \(ΔMNP\) nên theo tính chất trọng tâm tam giác ta có:

\(\begin{array}{l}
\dfrac{{MG}}{{MR}} = \dfrac{2}{3} \Rightarrow MG = \dfrac{2}{3}MR\\
\Rightarrow GR = MR - MG = MR - \dfrac{2}{3}MR = \dfrac{1}{3}MR
\end{array}\)

Từ đó suy ra: \(\dfrac{{GR}}{{MG}} = \dfrac{{\dfrac{1}{3}MR}}{{\dfrac{2}{3}MR}}= \dfrac{1}{2} \)\(\Rightarrow GR = \dfrac{1}{2}MG\)

Câu b:

\(NS =\dfrac{3}{2} NG;\) \(NS =3GS;\) \(NG =2GS.\)

Vì \(G\) là trọng tâm của \(ΔMNP\) nên theo tính chất trọng tâm tam giác ta có:

\(\begin{array}{l}
\dfrac{{NG}}{{NS}} = \dfrac{2}{3} \Rightarrow NG = \dfrac{2}{3}NS;NS = \dfrac{3}{2}NG\\
\Rightarrow GS = NS - NG = NS - \dfrac{2}{3}NS = \dfrac{1}{3}NS\\
\Rightarrow NS = 3GS\\
\dfrac{{NG}}{{GS}} = \dfrac{{\dfrac{2}{3}NS}}{{\dfrac{1}{3}NS}} = 2 \Rightarrow NG = 2GS
\end{array}\)

Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:

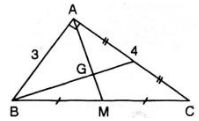
Cho tam giác vuông \(ABC\) có hai cạnh góc vuông \(AB = 3\,cm, AC = 4\,cm.\) Tính khoảng cách từ đỉnh \(A\) tới trọng tâm \(G\) của tam giác \(ABC.\)

Hướng dẫn giải

Áp dụng định lí Pitago cho \(∆ABC\) vuông tại \(A\) ta có:

\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& B{C^2} = {3^2} + {4^2} = 25 \cr} \)

\(\Rightarrow  BC = 5\,cm.\)

Gọi \(M\) là trung điểm của \(BC\) \(\Rightarrow \) \(AM\) là trung tuyến ứng với cạnh huyền \(BC\), do đó \(AM = \dfrac{1}{2} BC\)     (1) (Trong một tam giác vuông, đường trung tuyến ứng với cạnh bằng một nửa cạnh huyền).

Vì \(G\) là trọng tâm của \(∆ ABC\) nên \(AG =\dfrac{2}{3} AM\)       (2)

Thay (1) vào (2) ta được:

\( AG =\dfrac{2}{3}.\dfrac{1}{2} BC\)

\(\Rightarrow  AG = \dfrac{1}{3} BC = \dfrac{1}{3}.5  =\dfrac{5}{3}\,(cm).\)

Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.

Hướng dẫn giải

Giả sử \(∆ABC\) cân tại \(A\) có hai đường trung tuyến \(BM\) và \(CN\), ta chứng minh \(BM = CN.\) 

Vì \(∆ABC\) cân tại \(A\) nên \(AB = AC\)

Vì \(M, N\) lần lượt là trung điểm của \(2\) cạnh \(AC\) và \(AB\), suy ra:

\(AN = BN = AM = CM =\dfrac{AB}{2}\)\(\,= \dfrac{AC}{2}\).

Xét \(ΔBCM\) và \(ΔCBN\) có:

Cạnh \(BC\) chung

\(\widehat {BCM} = \widehat {CBN}\) (do \(ΔABC\) cân)

\(CM = BN\) (chứng minh trên)

Vậy \(ΔBCM = ΔCBN\) (c.g.c)

\(\Rightarrow   BM = CN\) (điều phải chứng minh).

Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Hướng dẫn giải

Ta đưa về bài toán: Cho \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G.\) Biết \(BM=CN\), chứng minh tam giác \(ABC\) là tam giác cân.

Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\)

\(\Rightarrow \) \(G\) là trọng tâm của tam giác \(ABC\).

\(\Rightarrow  GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\). 

Mà \(BM = CN\) (giả thiết) nên \(GB = GC.\)

Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\).

\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (Tính chất tam giác cân).

Xét \(∆BCN\) và \(∆CBM\) có: 

\(BC\) là cạnh chung

\(CN = BM\) (giả thiết)

\(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên)

Suy ra \(∆BCN = ∆CBM\) (c.g.c)

 \(\Rightarrow \) \(\widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng).

\(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân) (điều phải chứng minh).

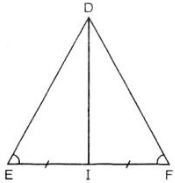
Cho tam giác \(DEF\) cân tại \(D\) với đường trung tuyến \(DI\).

a) Chứng minh \(∆DEI  = ∆DFI.\)

b) Các góc \(DIE\) và góc \(DIF\) là những góc gì?

c) Biết \(DE = DF = 13\,cm,\) \(EF = 10\,cm,\) hãy tính độ dài đường trung tuyến \(DI.\)

Hướng dẫn giải

a) Xét \(∆DEI\) và \(∆DFI\) có:

\(DI\) là cạnh chung

\(DE = DF\) (vì \( ∆DEF\) cân tại \(D\))

\(IE = IF\) (\(DI\) là trung tuyến)

Vậy \(∆DEI  = ∆DFI\) (c.c.c)

b) Vì  \(∆DEI  = ∆DFI\) (theo câu a) nên \(\widehat{DIE} =\widehat{DIF}\).

Mà \(\widehat{DIE} +\widehat{DIF} = 180^o\) ( hai góc kề bù)

\(\Rightarrow \) \(\widehat{DIE} =\widehat{DIF}\)\(=\dfrac{180^0}{2}= 90^o\) 

Vậy các góc \(DIE\) và góc \(DIF\) là những góc vuông.

c) \(I\) là trung điểm của \( EF\) nên \(IE = IF =\dfrac{{EF}}{2} = \dfrac{{10}}{2}= 5\,cm.\)

Áp dụng định lí Pytago vào \(∆DEI\) vuông tại \(I\) (do theo câu b góc \(DIE\) vuông) ta có: 

\(\eqalign{
& D{E^2} = D{I^2} + E{I^2} \cr
& \Rightarrow D{I^2} = D{E^2}-E{I^2} \cr
& \,\,\,\,\,\,\,\,D{I^2}\, = {13^2}-{5^2} = 144 \cr
& \Rightarrow DI = 12\,\,cm \cr} \)

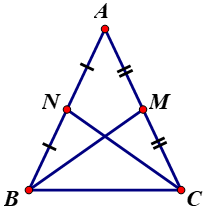
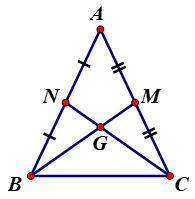
Cho \(G\) là trọng tâm của tam giác đều \(ABC.\) Chứng minh rằng:

                   \(GA = GB = GC.\)

Hướng dẫn: Áp dụng định lí ở bài tập \(26.\)

Hướng dẫn giải

Gọi \(M, N, P\) lần lượt là trung điểm của các cạnh \(BC, AC, AB.\)

Vì \(∆ABC\) là tam giác đều nên \(AB = AC = BC.\) 

Xét \(∆ABC\) có \(AB = AC\) nên \(∆ABC\) cân tại \(A\).

\( \Rightarrow  BN = CP\) (hai trung tuyến ứng với hai cạnh bên của tam giác cân thì bằng nhau theo định lí ở bài tập \(26\))

Ta có: \(GB = \dfrac{2}{3}BN;\,\,GC = \dfrac{2}{3}CP\)

Suy ra \( GB = GC = \dfrac{2}{3} BN = \dfrac{2}{3} CP\)   (1)

Xét \(∆ABC\) có \(BA = BC\) nên \(∆ABC\) cân tại \(B\).

\( \Rightarrow   CP = AM\)  (hai trung tuyến ứng với hai cạnh bên của tam giác cân thì bằng nhau theo định lí ở bài tập \(26\))

Ta có: \(GA = \dfrac{2}{3}AM;\,\,GC = \dfrac{2}{3}CP\)

Suy ra \(GC = GA = \dfrac{2}{3} CP = \dfrac{2}{3} AM\)   (2)

Từ (1) và (2) ta suy ra: \(GA = GB = GC\) (điều phải chứng minh).

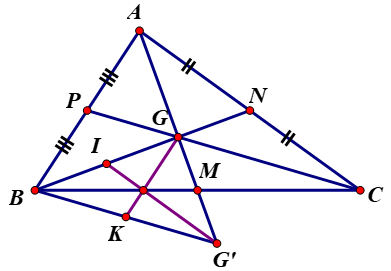
Gọi \(G\) là trọng tâm của tam giác \(ABC\). Trên tia \(AG\) lấy điểm \(G’\) sao cho \(G\) là trung điểm của \(AG’\).

a) So sánh các cạnh của tam giác \(BGG’\) với các đường trung tuyến của tam giác \(ABC.\)

b) So sánh các đường trung tuyến của tam giác \(BGG’\) với các cạnh của tam giác \(ABC.\)

Hướng dẫn giải

Câu a:

So sánh các cạnh của \(∆BGG’\) với các đường trung tuyến của \(∆ABC.\)

Gọi \(M, N, E\) lần lượt là trung điểm của \(BC, CA, AB.\)

\(G\) là trọng tâm của \(∆ABC\)

  \( \Rightarrow GA =\dfrac{2}{3}AM\)

Mà \(GA = GG’\) (\(G\) là trung điểm của \(AG’\))

  \( \Rightarrow GG' = \dfrac{2}{3} AM\)

- Vì \(G\) là trọng tâm của \(∆ABC\) \( \Rightarrow GB = \dfrac{2}{3} BN\)

- Ta có:  

\(GM =\dfrac{1}{2} AG\) (do \(G\) là trọng tâm) và \(AG = GG'\) (giả thiết)

\( \Rightarrow GM = \dfrac{1}{2} GG'\), do đó \(MG=MG'.\)

Xét \(∆GMC\) và \(∆G’MB\) có: 

\(GM = MG'\) (chứng minh trên)

\(MB = MC\) (\(M\) là trung điểm của \(BC\))

\( {\widehat {GMC} = \widehat {G'MB}} \) (hai góc đối đỉnh)

Vậy \( ∆GMC=∆G’MB\) (c.g.c)

 \( \Rightarrow BG' = CG\) (Hai cạnh tương ứng)

Mà \(CG = \dfrac{2}{3}  CE\) (\(G\) là trọng tâm tam giác \(ABC\)) 

 \( \Rightarrow BG' = \dfrac{2}{3} CE\)

Vậy \(GG' = \dfrac{2}{3}AM,GB = \dfrac{2}{3}BN,G'B = \dfrac{2}{3}CE\)

Hay mỗi cạnh của \(∆BGG’\) bằng  \(\dfrac{2}{3}\) đường trung tuyến của \(∆ABC.\)

Câu b:

So sánh các đường trung tuyến của \(∆BGG’\) với các cạnh của \(∆ABC.\)

- Ta có: \(BM\) là đường trung tuyến \(∆BGG’\)

Mà \(M\) là trung điểm của \(BC\) nên \(BM = \dfrac{1}{2} BC\).

Gọi \(I\) là trung điểm \(BG\) 

Vì \(IG = \dfrac{1}{2} BG\) (do \(I\) là trung điểm \(BG\))

\(GN = \dfrac{1}{2}BG\) (\(G\) là trọng tâm)

\( \Rightarrow  IG = GN\)

Xét  \(∆IGG’\) và \(∆NGA\) có:

\(IG = GN\) (chứng minh trên)

\(GG' = GA\) (giả thiết)

\(\widehat {IGG'} = \widehat {NGA}\) (hai góc đối đỉnh)

Vậy \(∆IGG’ = ∆NGA\) (c.g.c) 

\( \Rightarrow  IG' = AN\) (hai cạnh tương ứng)

\( \Rightarrow  IG' = \dfrac{{AC}}{2}\)

- Gọi \(K\) là trung điểm \(BG'\) \( \Rightarrow  GK\) là trung tuyến của \(∆BGG’\)

Vì \(GE = \dfrac{1}{2} GC\) (\(G\) là trọng tâm tam giác \(ABC\))

\(BG' = GC\) (chứng minh trên)

\( \Rightarrow  GE =\dfrac{1}{2} BG'\)

Mà \(K\) là trung điểm \(BG’\) \( \Rightarrow KG’ = EG\)

Vì \(∆GMC = ∆G’MB\) (chứng minh trên)

\( \Rightarrow\)   \(\widehat {GCM} = \widehat {G'BM}\) (hai góc tương ứng)

\( \Rightarrow  CE // BG’\) \( \Rightarrow\)   \(\widehat {AGE} = \widehat {AG'B}\) (đồng vị)

Xét \(∆AGE\) và \(∆GG’K\) có:

\(EG = KG’\) (chứng minh trên)

\(AG = GG'\) (giả thiết)

\(\widehat {AGE} = \widehat {AG'B}\) (chứng minh trên)

Vậy \(∆AGE = ∆GG’K\) (c.g.c)

\( \Rightarrow AE = GK\)

Mà \(AE = \dfrac{1}{2}AB\)

\(\Rightarrow  GK =  \dfrac{1}{2} AB\)

Vậy \(BM = \dfrac{1}{2}BC,G'I = \dfrac{1}{2}AC,GK = \dfrac{1}{2}AB\) 

Hay mỗi đường trung tuyến của \(∆BGG’\) bằng một nửa cạnh của tam giác \(ABC\).