Toán 12 Ôn tập chương 3: Phương pháp toạ độ trong không gian

a) Tọa độ của điểm và của vectơ

- Tọa độ của vectơ trong không gian 

Trong không gian Oxyz, cho vectơ \(\vec{u}\) tồn tại duy nhất bộ số \((x,y,z)\) sao cho: \(\overrightarrow{u}=(x;y;z)\)\(\Leftrightarrow \vec{u}=x\vec{i}+y\vec{j}+z\vec{k}.\)

Bộ số: \((x,y,z)\) được gọi là tọa độ của vectơ \(\vec{u}\).

- Tọa độ điểm trong không gian

Trong không gian Oxyz, cho điểm A tùy ý tồn tại duy nhất bộ số \((x_A,y_A,z_A)\) sao cho: \(A(x_A,y_A,z_A)\Leftrightarrow \overrightarrow{OA}=(x_A;y_A;z_A).\)

Bộ số \((x_A,y_A,z_A)\) được gọi là tọa độ điểm A.

b) Tích vô hướng

Công thức tính tích vô hướng: \(\vec{a}.\vec{b}=\left | \vec{a} \right |.\left | \vec{b} \right |.cos(\vec{a},\vec{b})\).

Biểu thức tọa độ của tích vô hướng: \(\left.\begin{matrix} \vec{a}=(x_1;y_1;z_1)\\ \vec{b}=(x_2;y_2;z_2) \end{matrix}\right\} \vec{a}.\vec{b} = x_1.x_2 + y_1.y_2 + z_1.z_2\).

Công thức tính góc giữa hai vectơ: \(cos(\vec a,\vec b) = \frac{{\vec a.\vec b}}{{\left| {\vec a} \right|.\left| {\vec b} \right|}}.\)

c) Phương trình mặt cầu

Trong không gian Oxyz, mặt cầu tâm I(a;b;c), bán kính R có phương trình: \((x-a)^2+(y-b)^2+(z-c)^2=R^2.\)

Nhận xét: Phương trình mặt cầu có thể viết dưới dạng \(x^2+y^2+z^2-2Ax-2By-2Cz+D=0\), điều kiện \(A^2+B^2+C^2-D> 0\).

Khi đó, mặt cầu có tâm \(I(A;B;C)\), bán kính \(R = \sqrt {{A^2} + {B^2} + {C^2} - D} .\)

a) Vectơ pháp tuyến của mặt phẳng

Cho mặt phẳng (P). Nếu vectơ \(\vec n\) khác \(\vec 0\) có giá vuông góc với (P) thì \(\vec n\) được gọi là Vectơ pháp tuyến của của (P).

b) Phương trình tổng quát của mặt phẳng

Phương trình tổng quát của mặt phẳng có dạng: \(Ax+By+Cz+D=0, \,\, A^2+B^2+C^2\neq 0)\).

Với \(\overrightarrow{n}=(A;B;C)\) là Vectơ pháp tuyến (VTPT).

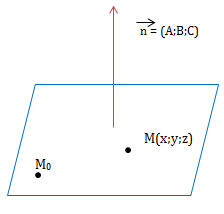
c) Viết phương trình mặt phẳng khi biết Vectơ pháp tuyến và một điểm thuộc mặt phẳng đó

Mặt phẳng (P) đi qua điểm \({{M_0}({x_0};{y_0};{z_0})}\), nhận vectơ \({\vec n = (A;B;C)}\) làm VTPT có phương trình tổng quát là:

\(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)

d) Phương trình mặt phẳng theo đoạn chắn

Mặt phẳng (P) đi qua A(a;0;0), B(0;b;0), C(0;0;c) có phương trình tổng quát là: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\).

a) Phương trình tham số của đường thẳng

Trong không gian, đường thẳng \(\Delta\) đi qua \(M(x_0,y_0,z_0)\) và nhận vectơ \(\vec u=(a,;b;c)\) làm Vectơ chỉ phương (VTCP) có phương trình tham số là: 

\(\Delta: \left\{\begin{matrix} x=x_0+at\\ y=y_0+bt\\ z=z_0+ct \end {matrix}\right.(t\in\mathbb{R})\) (t được gọi là tham số).

Nếu \(a,b,c \ne 0\) thì ta có phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}=t\).

Hay \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta\).

b) Vị trí tương đối giữa các đường thẳng

Trong không gian cho hai đường thẳng:  \(\Delta _1\) đi qua M1 và có một VTCP \(\overrightarrow{u_1}\), \(\Delta _2\) đi qua M2 và có một VTCP \(\overrightarrow{u_2}\).

Khi đó Vị trí tương đối giữa \(\Delta _1\) và \(\Delta _2\) được xác định như sau:

\(\Delta _1\) và \(\Delta _2\) chéo nhau \(\Leftrightarrow \left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ]. \overrightarrow{M_1.M_2}\neq 0\).

\(\Delta _1\) và \(\Delta _2\) cắt nhau \(\Leftrightarrow \left\{\begin{matrix} \left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ]. \overrightarrow{M_1.M_2}= 0\\ \overrightarrow{u_1}\neq k. \overrightarrow{u_2} \ \ \ \ \ \ \ \ \ \ \ \ \end{matrix}\right.\).

\(\Delta _1\) // \(\Delta _2\) \(\Leftrightarrow \left\{\begin{matrix} \overrightarrow{u_1}=k.\overrightarrow{u_2}\\ M_1\in \Delta _1, M_1\notin \Delta _2 \end{matrix}\right.\).

\(\Delta _1\equiv \Delta _2 \Leftrightarrow \left\{\begin{matrix} \overrightarrow{u_1}=k.\overrightarrow{u_2}\\ M_1\in \Delta _1, M_1\in \Delta _2 \end{matrix}\right.\).

Trong không gian với hệ tọa độ Oxyz , cho A(0;-3;-1) và B(-4;1;-3) và mặt phẳng \((P):x-2y+2z-7=0\).

a) Viết phương trình mặt phẳng (Q) đi qua gốc tọa độ, song song với AB và vuông góc với (P).

b) Lập phương trình mặt cầu nhận đoạn thẳng AB là đường kính.

Hướng dẫn giải

a) Ta có \(\overrightarrow{AB}=(-4;4;-2),\vec{n}=(1;-2;2)\) là véc tơ pháp tuyến của mặt phẳng (P).

\(\left [ \overrightarrow{AB};\vec{n} \right ]=(4;6;4)\)

(Q) là mặt phẳng đi qua gốc tọa độ O(0;0;0), (Q) song song với AB và vuông góc với mặt phẳng (P) suy ra mặt phẳng (Q) nhận \(\overrightarrow {{n_{(Q)}}} = \frac{1}{2}\left[ {\overrightarrow {AB} ;\vec n} \right] = (2;3;2)\) làm véctơ pháp tuyến.

Vậy phương trình mặt phẳng (Q) là: \(2x+3y+2z=0.\)

b) \(\overrightarrow{AB}=(-4;4;-2)\Rightarrow AB=\sqrt{16+16+4}=6\)

Trung điểm AB là I(-2;-1;-2).

Mặt cầu (S) có tâm I, bán kính \(R=\frac{AB}{2}=3\Rightarrow (S):(x+2)^2+(y+1)^2+(z+2)^2=9\).

Cho mặt cầu \((S): x^2+y^2+z^2-2x+6y+4z-22=0\) và \((\alpha ):x+2y-2z-8=0\). CRM: \((\alpha )\) cắt (S) theo một đường tròn. Xác định tâm, bán kính đường tròn đó.

Hướng dẫn giải

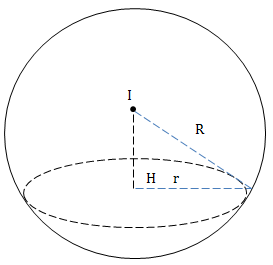
Nhận xét

Tâm đường tròn giao tuyến của mặt cầu S(I;R) và \((\alpha )\) là hình chiếu của I trên \((\alpha )\) với \(r^2+d^2(I;(\alpha ))=R^2\).

\((S): (x-1)^2+(y+3)^2+(z+2)^2=36\)

Mặt cầu (S) có tâm I(1;-3;-2), bán kính R = 6.

\(d(I;(\alpha ))=\frac{\left | 1-6+4-8 \right |}{\sqrt{1^2+2^2+(-2)^2}}=\frac{9}{3}=3\) Vậy \((\alpha )\) cắt mặt cầu theo 1 đường tròn.

Xác định tâm của H của đường tròn giao tuyến

Ta có H là hình chiếu của I trên \((\alpha )\).

Đường thẳng \(\Delta\) đi qua I và vuông góc với  \((\alpha )\), tức là nhận \(\vec{n_\alpha }=(1;2;-2)\) làm một VTCP có phương trình là:

\(\Delta \left\{\begin{matrix} x=1+t\\ y=-3+2t\\ z=-2-2t \end{matrix}\right.\)

\(H =\Delta \cap (\alpha )\)

\(H\in \Delta \Rightarrow H(1+t;-3+2t;-2-2t)\)

\(H\in (\alpha ) \Rightarrow 1+t+2(-3+2t)-2(-2-2t)-8=0\)

\(\Leftrightarrow 9t-9=0\Leftrightarrow t=1\)

Suy ra tọa độ H(2;-1;-4).

Bán kính đường trình giao tuyến: \(r^2=R^2-IH^2=36-9=27.\)

Vậy \(r=3\sqrt{3}.\)

Cho đường thẳng \(d:\frac{x-12}{4}=\frac{y-9}{3}=\frac{z-1}{1}\) và \((P):3x+5y-z-2=0\)

a) Tìm tọa độ giao điểm A của d và (P).

b) Viết phương trình (Q) đi qua M0(1;2;-1) và vuông góc với d.

c) Tìm tọa độ B' đối xứng với B(1;0;-1) qua (P).

Hướng dẫn giải

a) \(A=d\cap (P)\)

\(A\in d\left\{\begin{matrix} x=12+4t\\ y=9+3t\\ z=1+t \end{matrix}\right. \Rightarrow A(12+4t;9+3t;1+t)\)

\(A\in (P)\) nên \(3(12+4t)+5(9+3t)-(1+t)-2=0\)

\(\Leftrightarrow 26t +78t=0\Leftrightarrow t=-3\)

Vậy tọa độ là A(0;0;-2).

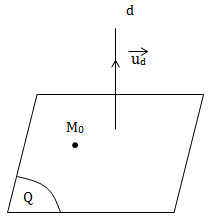
b) \((Q)\perp d\) nên (Q) nhận \(\vec{u_d}=(4;3;1)\) làm một VTPT.

Phương trình mặt phẳng (Q) là \((Q):4(x-1)+3(y-2)+1(z+1)=0\) hay \(4x+3y+z-9=0.\)

c) Viết phương trình \(\Delta\) đi qua B và vuông góc (P)

\(\Delta\) \(\perp\) (P) nên \(\Delta\) nhận \(\vec{n_P}=(3;5;-1)\) làm một VTCP.

Phương trình tham số của \(\Delta: \left\{\begin{matrix} x=1+3t\\ y=5t\\ z=-1-t \end{matrix}\right.\)

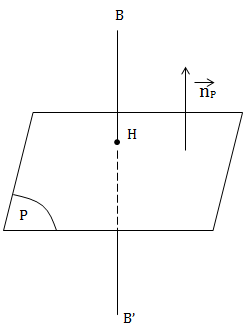
H là hình chiếu của B trên (P)

\(H=\Delta \cap (P)\)

\(H\in \Delta \Rightarrow H(1+3t;5t;-1-t)\)

\(H\in(P)\) nên \(3(1+3t)+25t+1+t-2=0\)

\(\Leftrightarrow 35t+2=0\)

\(\Leftrightarrow t=-\frac{2}{35}\)

\(H\left ( \frac{29}{35};-\frac{2}{7};-\frac{33}{35} \right )\)

H là trung điểm BB' nên: \(\left\{\begin{matrix} x_{B'}=2x_H-x_B=\frac{23}{35}\\ \\ y_{B'}=2y_H-y_B=-\frac{4}{7}\\ \\ z_{B'}=2z_H-z_B=\frac{2}{35} \end{matrix}\right.\)

Vậy tọa độ \(B' \left ( \frac{23}{35};-\frac{4}{7};\frac{2}{35} \right ).\)

Câu 1: Cho hệ toạ độ \(Oxyz\), cho bốn điểm \(A( 1 ; 0 ; 0 ), B( 0 ; 1 ; 0 ), C( 0 ; 0 ; 1 ), D( -2 ; 1 ; -1)\)

a) Chứng minh \(A, B, C, D\) là bốn đỉnh của một tứ diện.

b) Tìm góc giữa hai đường thẳng \(AB\) và \(CD\).

c) Tính độ dài đường cao của hình chóp \(A.BCD\).

Câu 2: Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với đường thẳng d:  \(\dfrac{{x - 3}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{3}\)

Câu 3: Trong hệ toạ độ \(Oxyz\), cho mặt cầu \((S)\) có đường kính là \(AB\) biết rằng \(A( 6 ; 2 ; -5), B(-4 ; 0 ; 7)\).

a) Tìm toạ độ tâm \(I\) và tính bán kính \(r\) của mặt cầu \((S)\)

b) Lập phương trình của mặt cầu \((S)\).

c) Lập phương trình của mặt phẳng \((α)\) tiếp xúc với mặt cầu \((S)\) tại điểm \(A\).

Câu 4: Lập phương trình mặt phẳng (P)  đi qua điểm M(1; -3; 2) và song song với mặt phẳng \((Q): x – z = 0\).

Câu 5: Lập phương trình mặt phẳng (P) đi qua ba điểm A(-1; -3; 2), B(-2; 1; 1) và C(0; 1; -1).

Câu 1: Trong không gian với hệ trục Oxyz, cho đường thẳng \(\left( d \right):x - 1 = \frac{{y - 2}}{2} = \frac{{z - 4}}{3}\) và song song với mặt phẳng \(\left( P \right):x + 4y + 9z - 9 = 0.\) Tìm giao điểm I của (d ) và (P).

A.  I(2;4;-1)

B. I(1;2;0)

C.  I(1;0;0)

D. I(0;0;1)

Câu 2: Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị thực của m để đường thẳng \(\Delta :\frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z + 1}}{1}\) song song với mặt phẳng (P): \(x + y - z + m = 0.\)

A.  \(m\neq 0\)

B.  \(m=0\)

C.  \(m\in \mathbb{R}\)

D. Không có giá trị nào của m

Câu 3: Trong không gian Oxyz, cho đường thẳng \(\left( \Delta \right):\frac{{x - 1}}{2} = \frac{{y + 1}}{1} = \frac{{z - 2}}{1}\). Tìm hình chiếu vuông góc của \(\left( \Delta \right)\) trên mặt phẳng (Oxy).

A.  \(\left\{ \begin{array}{l} x = 0\\ y = - 1 - t\\ z = 0 \end{array} \right.\)

B.  \(\left\{ \begin{array}{l} x = 1 + 2t\\ y = - 1 + t\\ z = 0 \end{array} \right.\) 

C.  \(\left\{ \begin{array}{l} x = - 1 + 2t\\ y = 1 + t\\ z = 0 \end{array} \right.\)

D.  \(\left\{ \begin{array}{l} x = - 1 + 2t\\ y = - 1 + t\\ z = 0 \end{array} \right.\)

Câu 4: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(d:\frac{{x - 1}}{1} = \frac{y}{1} = \frac{{z + 1}}{2}\) và điểm \(I\left( {1;0;2} \right).\) Viết phương trình mặt cầu tâm I và tiếp xúc với đường thẳng d.

A. \({\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = 3\)

B.  \({\left( {x + 1} \right)^2} + {y^2} + {\left( {z + 2} \right)^2} = 3\)

C. \({\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = 19\)

D. \({\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = 9\)

Câu 5: Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;3;-2) và đường thẳng \(\Delta :\frac{{x - 4}}{1} = \frac{{y - 4}}{2} = \frac{{z + 3}}{{ - 1}}\). Viết phương trình mặt cầu (S) có tâm là điểm I và cắt  tại hai điểm phân biệt A, B sao cho đoạn thẳng AB có độ dài bằng 4.

A. \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 9\)

B. \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 9\)

C. \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 2} \right)^2} = 9\)

D. \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 2} \right)^2} = 9\)

Câu 6: Trong không gian Oxyz cho mặt phẳng \(\left( P \right):x + y + z - 1 = 0\) và hai điểm \(A\left( {1; - 3;0} \right),B\left( {5; - 1; - 2} \right)\). Tìm tọa độ điểm M trên mặt phẳng (P) sao cho \(\left| {MA - MB} \right|\) đạt giá trị lớn nhất ?

A. \(M\left( { - 2; - 3;3} \right)\)

B. \(M\left( { - 2; - 3;2} \right)\)

C. \(M\left( { - 2; - 3;6} \right)\)

D. \(M\left( { - 2; - 3;0} \right)\)

Qua bài học này, học sinh nắm được một số nội dung chính như sau:

• Nắm được các khái niệm về toạ độ của điểm ,của vectơ
• Nắm vững các tính chất , công thức tính khoảng cách , tích vô hướng, góc
• Biết liên hệ giữa các công thức trong mặt phẳng và trong không gian
• Biết cách tìm toạ độ của một vectơ, một điểm . Tính dược khoảng cách giữa hai điểm , góc giữa hai vectơ , tính được tích vô hướng và cá yếu tố liên quan