Giải bài tập SBT Toán 11 Bài 2: Hai đường thẳng vuông góc

Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng: $\overrightarrow {G{\rm{D}}}.\overrightarrow {GA} + \overrightarrow {G{\rm{D}}}.\overrightarrow {GB} + \overrightarrow {G{\rm{D}}}.\overrightarrow {GC} = 0$

Phương pháp giải:

Đặt nhân tử chung và sử dụng công thức: G là trọng tâm của tam giác ABC nên $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0.$

Hướng dẫn giải:

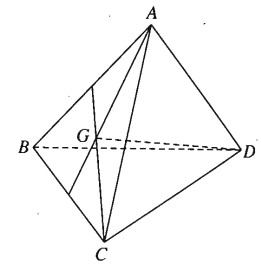
Ta có:

$\eqalign{ & \overrightarrow {G{\rm{D}}}.\overrightarrow {GA} + \overrightarrow {GD}.\overrightarrow {GB} + \overrightarrow {GD}.\overrightarrow {GC} \cr & = \overrightarrow {GD}.\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) \cr & = \overrightarrow {GD}.\overrightarrow 0 = 0 \cr}$

(Vì G là trọng tâm của tam giác ABC nên $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0$)

Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, AD và có MN = PQ. Chứng minh rằng AB ⊥ CD.

Phương pháp giải:

Ta cần chứng minh $\overrightarrow {AB}.\overrightarrow {C{\rm{D}}} = 0$

Hướng dẫn giải:

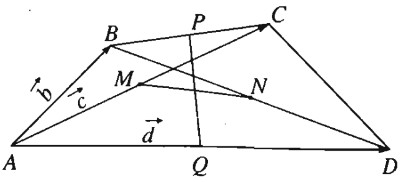
Ta cần chứng minh $\displaystyle \overrightarrow {AB}.\overrightarrow {C{\rm{D}}} = 0$

Đặt $\displaystyle \overrightarrow {AB} = \overrightarrow b,\,\,\overrightarrow {AC} = \overrightarrow c,\,\,\overrightarrow {AD} = \overrightarrow d$. Ta có:

$\displaystyle \overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AN} \displaystyle = - {1 \over 2}\overrightarrow {AC} + {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)$

Suy ra $\displaystyle \overrightarrow {MN} = {1 \over 2}\left( {\overrightarrow b + \overrightarrow d - \overrightarrow c } \right)$

$\displaystyle \eqalign{ & \overrightarrow {QP} = \overrightarrow {QA} + \overrightarrow {AP} \cr & = - {1 \over 2}\overrightarrow {A{\rm{D}}} + {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) \cr & = {1 \over 2}\left( {\overrightarrow b + \overrightarrow c - \overrightarrow d } \right) \cr}$

Theo giả thiết ta có: $\displaystyle MN = PQ \Leftrightarrow {\overrightarrow {MN} ^2} = {\overrightarrow {QP} ^2}$

$\displaystyle \eqalign{ & {\left( {\overrightarrow b + \overrightarrow d - \overrightarrow c } \right)^2} = {\left( {\overrightarrow b + \overrightarrow c - \overrightarrow d } \right)^2} \cr & \Leftrightarrow \overrightarrow b.\overrightarrow d - \overrightarrow b.\overrightarrow c = \overrightarrow b.\overrightarrow c - \overrightarrow b.\overrightarrow d \cr & \Leftrightarrow 2\overrightarrow b.\overrightarrow d - 2\overrightarrow b.\overrightarrow c = 0 \cr & \Leftrightarrow \overrightarrow b.\left( {\overrightarrow d - \overrightarrow c } \right) = 0 \cr & \Leftrightarrow \overrightarrow {AB}.\left( {\overrightarrow {A{\rm{D}}} - \overrightarrow {AC} } \right) = 0 \cr & \Leftrightarrow \overrightarrow {AB}.\overrightarrow {C{\rm{D}}} = 0 \Leftrightarrow \overrightarrow {AB} \bot \overrightarrow {C{\rm{D}}} \cr}$

Vậy AB ⊥ CD.

Cho hình chóp tam giác S.ABC có SA = SB = SC = AB = AC = a và $BC = a\sqrt 2$. Tính góc giữa hai vectơ $\overrightarrow {AB}$ và $\overrightarrow {SC}$.

Phương pháp giải:

Sử dụng công thức $\displaystyle \cos \left( {\overrightarrow {SC},\overrightarrow {AB} } \right) = {{\overrightarrow {SC}.\overrightarrow {AB} } \over {\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}}$ → $\left( {\overrightarrow {SC},\overrightarrow {AB} } \right)$

Hướng dẫn giải:

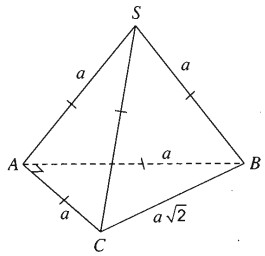
Ta tính côsin của góc giữa hai vectơ $\displaystyle \overrightarrow {SC}$ và $\displaystyle \overrightarrow {AB}$. Ta có

$\displaystyle \eqalign{ & \cos \left( {\overrightarrow {SC},\overrightarrow {AB} } \right) = {{\overrightarrow {SC}.\overrightarrow {AB} } \over {\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}} \cr & = {{\left( {\overrightarrow {SA} + \overrightarrow {AC} } \right).\overrightarrow {AB} } \over {{a^2}}} \cr & = {{\overrightarrow {SA}.\overrightarrow {AB} + \overrightarrow {AC}.\overrightarrow {AB} } \over {{a^2}}} \cr}$

Theo giả thiết ta suy ra hình chóp có các tam giác đều là SAB, SAC và các tam giác vuông là ABC vuông tại A và SBC vuông tại S.

Do đó $\displaystyle \overrightarrow {SA}.\overrightarrow {AB} = a.a.\cos 120^\circ = - {{{a^2}} \over 2}$ và $\displaystyle \overrightarrow {AC}.\overrightarrow {AB} = 0$

Vậy $\displaystyle \cos \left( {\overrightarrow {SC},\overrightarrow {AB} } \right) = {{ - {{{a^2}} \over 2} + 0} \over {{a^2}}} = - {1 \over 2}$

Hay $\displaystyle \left( {\overrightarrow {SC},\overrightarrow {AB} } \right) = {120^0}$

Vậy góc giữa hai vectơ $\displaystyle \overrightarrow {AB}$ và $\displaystyle \overrightarrow {SC}$ bằng 120°.

Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và $BC = a\sqrt 2$. Tính góc giữa hai đường thẳng AB và SC.

Phương pháp giải:

Sử dụng công thức: $\cos \left( {\overrightarrow {SC},\overrightarrow {AB} } \right) = {{\overrightarrow {SC}.\overrightarrow {AB} } \over {\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}}$ → $\left( {\overrightarrow {SC},\overrightarrow {AB} } \right)$

Hướng dẫn giải:

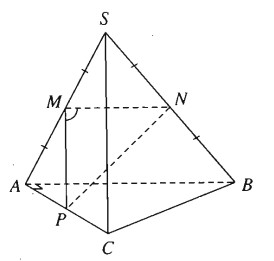
- Cách thứ nhất

Dễ thấy tam giác ABC vuông tại A nên $\overrightarrow {AC}.\overrightarrow {AB} = 0$ và tam giác SAB đều nên $\left( {\overrightarrow {SA},\overrightarrow {AB} } \right) = {120^0}.$

$\eqalign{ & \overrightarrow {SC}.\overrightarrow {AB} = \left( {\overrightarrow {SA} + \overrightarrow {AC} } \right).\overrightarrow {AB} \cr & = \overrightarrow {SA}.\overrightarrow {AB} + \overrightarrow {AC}.\overrightarrow {AB} \cr & \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AB} } \right|.\cos 120^\circ = - {{{a^2}} \over 2} \cr & \Rightarrow \cos \left( {\overrightarrow {SC},\overrightarrow {AB} } \right) = {{\overrightarrow {SC}.\overrightarrow {AB} } \over {\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}} \cr & = {{ - {{{a^2}} \over 2}} \over {{a^2}}} = - {1 \over 2} \cr}$

Do đó góc giữa hai đường thẳng SC và  AB bằng 60°.

- Cách thứ hai

Gọi M, N, P lần lượt là trung điểm của SA, SB, AC. Để tính góc giữa hai đường thẳng SC và AB, ta cần tính $\widehat {NMP}$.

Ta có

$NB = MP = {a \over 2},S{P^2} = {{3{a^2}} \over 4},B{P^2} = {{5{a^2}} \over 4} \\P{B^2} + S{P^2} = 2N{P^2} + {{S{B^2}} \over 2} \Rightarrow N{P^2} = {{3{{\rm{a}}^2}} \over 4}$

Mặt khác:

$N{P^2} = N{M^2} + M{P^2} - 2MN.MP\cos \widehat {NMP} \\ \Rightarrow \cos \widehat {NMP} = - {{{{{a^2}} \over 4}} \over {2.{a \over 2}.{a \over 2}}} = - {1 \over 2} \Rightarrow \widehat {NMP} = {120^0}$

Vậy góc giữa hai đường thẳng SC và AB bằng 60°.

Chứng minh rằng một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

Phương pháp giải:

Chứng minh góc giữa hai đường thẳng bằng 90^o.

Hướng dẫn giải:

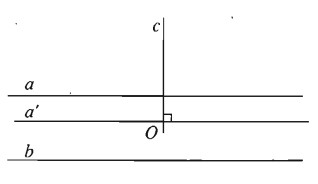
Giả sử a // b và c $\bot$ a. Lấy điểm O bất kì trên c, kẻ a' // a qua O suy ra $\widehat {cOa'} = {90^0}.$

Dễ thấy a' // b nên $\widehat {cOa'}$ chính là góc giữa hai đường thẳng c và b, do đó c $\bot$ b.

Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau (hình hộp như vậy còn được gọi là hình hộp thoi). Chứng minh rằng AC ⊥ B’D’.

Phương pháp giải:

Sử dụng kết quả bài 3.12: "Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia"

Hướng dẫn giải:

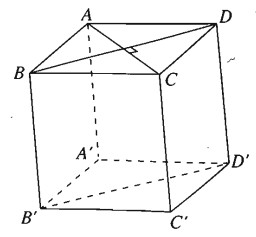
Từ giả thiết suy ra tứ giác ABCD là hình thoi, do đó AC ⊥ BD

Dễ thấy mặt chéo BDD’B’ của hình hộp đã cho là hình bình hành, do đó BD // B'D'.

Từ đó, theo bài 3.12 suy ra AC ⊥ B’D’.

Cho hình hộp thoi ABCD.A’B’C’D’ có tất cả các cạnh bằng a và $\widehat {ABC} = \widehat {B'BA} = \widehat {B'BC} = {60^0}$. Chứng minh tứ giác A’B’CD là hình vuông.

Phương pháp giải:

Chứng minh A'B'CD là hình thoi có 1 góc vuông.

Hướng dẫn giải:

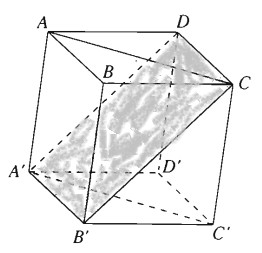
Trước hết dễ thấy tứ giác A’B’CD là hình bình hành, ngoài ra B'C = a = CD nên nó là hình thoi.

Ta chứng minh hình thoi A’B’CD là hình vuông. Ta có:

$\eqalign{ & \overrightarrow {CB'}.\overrightarrow {CD} = \left( {\overrightarrow {CB} + \overrightarrow {BB'} } \right).\overrightarrow {BA} \cr & = \overrightarrow {CB}.\overrightarrow {BA} + \overrightarrow {BB'}.\overrightarrow {BA} \cr & = - {{{a^2}} \over 2} + {{{a^2}} \over 2} = 0 \cr}$

Vậy tứ giác A’B’CD là hình vuông.

Cho tứ diện ABCD trong đó $AB \bot AC,AB \bot B{\rm{D}}$. Gọi P và Q lần lượt là trung điểm của AB và CD. Chứng minh rằng AB và PQ vuông góc với nhau.

Phương pháp giải:

Kiểm tra tích vô hướng $\overrightarrow {PQ}.\overrightarrow {AB}=0$ và kết luận.

Hướng dẫn giải:

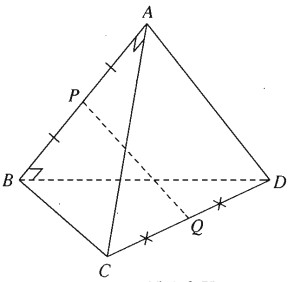
$\eqalign{ & \overrightarrow {PQ} = \overrightarrow {PA} + \overrightarrow {AC} + \overrightarrow {CQ} \,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr & \overrightarrow {PQ} = \overrightarrow {PB} + \overrightarrow {B{\rm{D}}} + \overrightarrow {DQ} \,\,\,\,\,\,\,\,\,\,\left( 2 \right) \cr}$

Cộng từng vế (1) và (2) ta có:

$2\overrightarrow {PQ} = \overrightarrow {AC} + \overrightarrow {B{\rm{D}}}$

Suy ra $2\overrightarrow {PQ}.\overrightarrow {AB} = \overrightarrow {AC}.\overrightarrow {AB} + \overrightarrow {B{\rm{D}}}.\overrightarrow {AB} = 0$

Hay $\overrightarrow {PQ}.\overrightarrow {AB} = 0$, tức là PQ $\bot$ AB.