Giải bài tập SGK Toán 8 Bài 3: Tính chất đường phân giác của tam giác
Môn Toán là môn quan trọng và tương đối khó với các em học sinh lớp 8, với mong muốn giúp các em nắm thật vững kiến thức và làm bài thật hiệu quả eLib đã biên soạn và tổng hợp nội dung giải bài tập SGK trang 67, 68 bên dưới đây. Với nội dung chi tiết, rõ ràng được trình bày logic, khoa học hứa hẹn sẽ mang lại cho các em thật nhiều kiến thức bổ ích. Mời các em cùng tham khảo!
Mục lục nội dung

1. Giải bài 15 trang 67 SGK Toán 8 tập 2
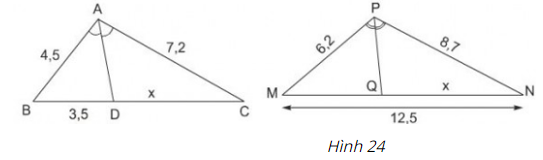
Tính \(x\) trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất.
Phương pháp giải
Hình ABC
\(AD\) là tia phân giác góc \(A\) của \(∆ABC\)
\(\dfrac{BD}{AB} = \dfrac{DC}{AC}\)
Suy ra tính được DC = x
Hình PMN
\(PQ\) là đường phân giác góc \(P\) của \(∆PMN\) (gt) nên \(\dfrac{MQ}{MP}= \dfrac{NQ}{NP}\)
Hay \(\dfrac{MQ}{6,2} = \dfrac{x}{8,7}\)
Từ đó suy ra được x
Hướng dẫn giải
Hình ABC
\(AD\) là tia phân giác góc \(A\) của \(∆ABC\) (gt) nên áp dụng tính chất của đường phân giác trong tam giác ta có:
\(\dfrac{BD}{AB} = \dfrac{DC}{AC}\)
\(\Rightarrow DC = \dfrac{BD.AC}{AB}= \dfrac{3,5.7,2}{4,5}\)
\(\Rightarrow x = 5,6\)
Hình PMN
\(PQ\) là đường phân giác góc \(P\) của \(∆PMN\) (gt) nên
\(\dfrac{MQ}{MP}= \dfrac{NQ}{NP}\) (tính chất đường phân giác của tam giác)
Hay \(\dfrac{MQ}{6,2} = \dfrac{x}{8,7}\)
Có: \(MN=MQ+x=12,5\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\Rightarrow \dfrac{x}{8,7} = \dfrac{MQ}{6,2} = \dfrac{x + MQ}{8,7+ 6,2}= \dfrac{12,5}{14,9}\)
\( \Rightarrow x = \dfrac{{12,5.8,7}}{{14,9}} \approx 7,3\)
2. Giải bài 16 trang 67 SGK Toán 8 tập 2
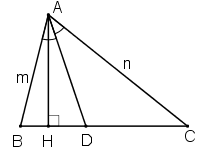
Tam giác \(ABC\) có độ dài các cạnh \(AB= m, AC= n\) và \(AD\) là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác \(ABD\) và diện tích tam giác \(ACD\) bằng \(\dfrac{m}{n}\).
Phương pháp giải
Kẻ \(AH ⊥ BC\)
Chứng tỏ: \(\dfrac{S_{ABD}}{S_{ACD}} = \dfrac{BD}{DC}\)
Mặt khác: \(AD\) là đường phân giác của \(∆ABC\) (gt)
\( \Rightarrow \dfrac{BD}{DC}= \dfrac{AB}{AC} = \dfrac{m}{n}\)
Vậy \(\dfrac{S_{ABD}}{S_{ACD}} = \dfrac{m}{n}\)
Hướng dẫn giải
Kẻ \(AH ⊥ BC\)
Ta có:
\({S_{ABD}} = \dfrac{1}{2}AH.BD\)
\({S_{ACD}} = \dfrac{1}{2}AH.DC\)
\( \Rightarrow \dfrac{S_{ABD}}{S_{ACD}} = \dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.DC} = \dfrac{BD}{DC}\)
Mặt khác: \(AD\) là đường phân giác của \(∆ABC\) (gt)
\( \Rightarrow \dfrac{BD}{DC}= \dfrac{AB}{AC} = \dfrac{m}{n}\) (tính chất đường phân giác của tam giác)
Vậy \(\dfrac{S_{ABD}}{S_{ACD}} = \dfrac{m}{n}\) (điều phải chứng minh).
3. Giải bài 17 trang 68 SGK Toán 8 tập 2
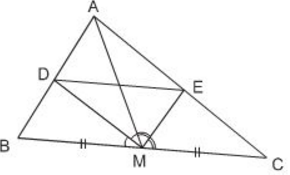
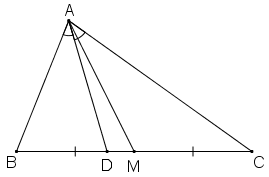
Cho tam giác \(ABC\) với đường trung tuyến \(AM\). Tia phân giác của góc \(AMB\) cắt cạnh \(AB\) ở \(D\), tia phân giác của góc \(AMC\) cắt cạnh \(AC\) ở \(E\). Chứng minh rằng \(DE // BC\) (h25)
Phương pháp giải
Ta có \(MD\) là đường phân giác góc \(M\) của tam giác \(ABM\) (giả thiết)
\(\Rightarrow \dfrac{AD}{BD} = \dfrac{AM}{BM}\) (1)
Tương tự ta có: \(\dfrac{AE}{CE}= \dfrac{AM}{MC}\) (2); \(\dfrac{AM}{BM} = \dfrac{AM}{MC}\) (3)
Từ (1), (2), (3) \(\Rightarrow \dfrac{AD}{BD}= \dfrac{AE}{CE}\)
Vậy \(DE // BC\)
Hướng dẫn giải
Ta có \(MD\) là đường phân giác góc \(M\) của tam giác \(ABM\) (giả thiết)
\(\Rightarrow \dfrac{AD}{BD} = \dfrac{AM}{BM}\) (1) (tính chất đường phân giác của tam giác)
\(ME\) là đường phân giác góc \(M\) của tam giác \(ACM\) (giả thiết)
\(\Rightarrow \dfrac{AE}{CE}= \dfrac{AM}{MC}\) (2) (tính chất đường phân giác của tam giác)
Mà \(MB = MC\) (vì \(AM\) là đường trung tuyến nên M là trung điểm của \(BC\))
\( \Rightarrow \dfrac{AM}{BM} = \dfrac{AM}{MC}\) (3)
Từ (1), (2), (3) \(\Rightarrow \dfrac{AD}{BD}= \dfrac{AE}{CE}\)
\( \Rightarrow DE // BC\) ( theo định lí Talet đảo).
4. Giải bài 18 trang 68 SGK Toán 8 tập 2
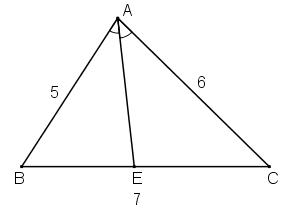
Tam giác \(ABC\) có \(AB= 5cm, AC= 6cm, BC= 7cm.\) Tia phân giác của góc \(BAC\) cắt \(BC\) tại \(E\). Tính các đoạn \(EB, EC\).
Phương pháp giải
Xét tam giác ABC có: \(\dfrac{EB}{AB} = \dfrac{EC}{AC}\)
Áp dụng tính chất của dãy tỉ số bằng ta được:
\(\dfrac{EB}{AB} = \dfrac{EC}{AC} = \dfrac{EB+EC}{AB+AC}\)\(\, = \dfrac{BC}{AB+AC}\)
Từ đó tính được \(EB, EC\).
Hướng dẫn giải
\(AE\) là đường phân giác của \(\widehat {BAC}\) (giả thiết) nên xét tam giác ABC có:
\(\dfrac{EB}{AB} = \dfrac{EC}{AC}\) (tính chất đường phân giác của tam giác)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{EB}{AB} = \dfrac{EC}{AC} = \dfrac{EB+EC}{AB+AC}\)\(\, = \dfrac{BC}{AB+AC}\)
\( \Rightarrow EB = \dfrac{AB.BC}{AB+AC} = \dfrac{5.7}{5+6} =\dfrac{35}{11}\)
\(EC = BC- EB =7-\dfrac{35}{11} =\dfrac{42}{11}\)
5. Giải bài 19 trang 68 SGK Toán 8 tập 2
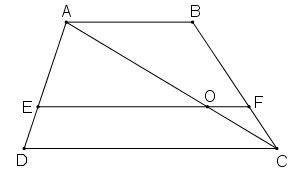
Cho hình thang \(ABCD\) (\(AB // CD\)).
Đường thẳng \(a\) song song với \(DC\), cắt các cạnh \(AD\) và \(BC\) theo thứ tự là \(E\) và \(F.\)
Chứng minh rằng:
a) \(\dfrac{AE}{ED} = \dfrac{BF}{FC}\);
b) \(\dfrac{AE}{AD} = \dfrac{BF}{BC}\)
c) \(\dfrac{DE}{DA} = \dfrac{CF}{CB}\).
Phương pháp giải
a) Chứng minh \(\dfrac{AE}{ED} = \dfrac{AO}{OC}\) (1) và \(\dfrac{AO}{OC} = \dfrac{BF}{FC}\) (2)
Từ (1) và (2) \(\Rightarrow \dfrac{AE}{ED} = \dfrac{BF}{FC}\)
b) Theo câu a) có: \({{AE} \over {ED}} = {{BF} \over {FC}}\) từ đó chứng minh \({{BC} \over {BF}} = {{AD} \over {AE}}\) \(\Rightarrow {{AE} \over {AD}} = {{BF} \over {BC}}\)
c) Theo câu b) có: \({{AE} \over {ED}} = {{BF} \over {FC}}\) từ đó chứng minh \({{AD} \over {ED}} = {{BC} \over {FC}}\) suy ra \({{DE} \over {DA}} = {{CF} \over {CB}}\)
Hướng dẫn giải
a) Nối \(AC\) cắt \(EF\) tại \(O\)
\(∆ADC\) có \(EO // DC\) (giả thiết) \( \Rightarrow \dfrac{AE}{ED} = \dfrac{AO}{OC}\) (1) (theo định lí Talet)
\(∆ABC\) có \(OF // AB\) (giả thiết) \( \Rightarrow \dfrac{AO}{OC} = \dfrac{BF}{FC}\) (2) (theo định lí Talet)
Từ (1) và (2) \(\Rightarrow \dfrac{AE}{ED} = \dfrac{BF}{FC}\)
b) Theo câu a) ta có:
\(\eqalign{
& {{AE} \over {ED}} = {{BF} \over {FC}} \Rightarrow {{FC} \over {BF}} = {{ED} \over {AE}} \cr
& \Rightarrow {{FC} \over {BF}} + 1 = {{ED} \over {AE}} + 1 \cr
& \Rightarrow {{FC + BF} \over {BF}} = {{ED + AE} \over {AE}} \cr
& \Rightarrow {{BC} \over {BF}} = {{AD} \over {AE}} \cr
& \Rightarrow {{AE} \over {AD}} = {{BF} \over {BC}} \cr} \)
c) Theo câu b) ta có:
\(\eqalign{
& {{AE} \over {ED}} = {{BF} \over {FC}} \cr
& \Rightarrow {{AE} \over {ED}} + 1 = {{BF} \over {FC}} + 1 \cr
& \Rightarrow {{AE + ED} \over {ED}} = {{BF + FC} \over {FC}} \cr
& \Rightarrow {{AD} \over {ED}} = {{BC} \over {FC}} \cr
& \Rightarrow {{FC} \over {BC}} = {{ED} \over {AD}}\,\,\,hay\,\,{{DE} \over {DA}} = {{CF} \over {CB}} \cr} \)
6. Giải bài 20 trang 68 SGK Toán 8 tập 2
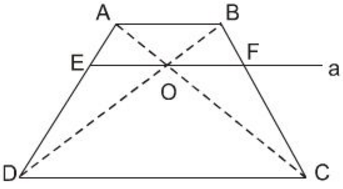
Cho hình thang \(ABCD\; (AB //CD)\). Hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Đường thẳng \(a\) qua \(O\) và song song với đáy của hình thang cắt các cạnh \(AD, BC\) theo thứ tự \(E\) và \(F\) (h26)
Chứng minh rằng \(OE = OF\).
Phương pháp giải
Chứng minh: \(\dfrac{OE}{DC} = \dfrac{AO}{AC}\) (1); \(\dfrac{OF}{DC} = \dfrac{BF}{BC}\) (2); \(\dfrac{AO}{AC} = \dfrac{BF}{BC}\) (3)
Từ (1), (2), (3) suy ra \(\dfrac{OE}{DC} = \dfrac{OF}{DC}\) nên \(OE = OF\).
Hướng dẫn giải
\(∆ADC\) có \(OE // DC\) (gt) nên \(\dfrac{OE}{DC} = \dfrac{AO}{AC}\) (1) (hệ quả của định lí TaLet trong tam giác)
\(∆BDC\) có \(OF // DC\) (gt) nên \(\dfrac{OF}{DC} = \dfrac{BF}{BC}\) (2) (hệ quả của định lí TaLet trong tam giác)
\(∆BAC\) có \(OF // AB\) (gt) nên \(\dfrac{AO}{AC} = \dfrac{BF}{BC}\) (3) (hệ quả của định lí TaLet trong tam giác)
Từ (1), (2), (3) suy ra \(\dfrac{OE}{DC} = \dfrac{OF}{DC}\) nên \(OE = OF\).
7. Giải bài 21 trang 68 SGK Toán 8 tập 2
a) Cho tam giác \(ABC\) với đường trung tuyến \(AM\) và đường phân giác \(AD\). Tính diện tích tam giác \(ADM\), biết \(AB= m, AC= n\;( n>m)\) và diện tích của tam giác \(ABC\) là \(S\).
b) Cho \(n = 7cm, m = 3cm\). Hỏi diện tích tam giác \(ADM\) chiếm bao nhiêu phần trăm diện tích tam giác \(ABC\).
Phương pháp giải
a) Chỉ ra được \(\dfrac{S_{ABD}}{S_{ADC}} = \dfrac{DB}{DC}= \dfrac{AB}{AC}= \dfrac{m}{n}\)
Chứng minh: \(\dfrac{S_{ABD}}{S_{ABC}}= \dfrac{m}{n+m}\)
Vì \(AM\) là trung tuyến của \(∆ABC\) (gt) \(\Rightarrow S_{ABM}= \dfrac{1}{2}S_{ABC}\).
Có \(AB < AC( m<n)\) vì \(AD\) là đường phân giác, \(AM\) là đường trung tuyến kẻ từ \(A\) nên \(AD\) nằm giữa \(AB\) và \(AM\).
Từ đó chưng minh được: \(S_{ADM}= \dfrac{S(n -m)}{2(m+n)}\) (với \(n>m\))
b) \({S_{A{\rm{D}}M}} = \dfrac{{7 - 3}}{{2\left( {7 + 3} \right)}}.S\)
Hướng dẫn giải
a) Ta có \(AD\) là đường phân giác của \(∆ABC\) (gt) nên
\(\dfrac{{B{\rm{D}}}}{{DC}} = \dfrac{{AB}}{{AC}}\) (Tính chất đường phân giác của tam giác)
\(\dfrac{S_{ABD}}{S_{ADC}} = \dfrac{DB}{DC}\) (do hai tam giác có chung chiều cao từ đỉnh A)
Nên \(\dfrac{S_{ABD}}{S_{ADC}} = \dfrac{DB}{DC}= \dfrac{AB}{AC}= \dfrac{m}{n}\)
\(\eqalign{
& \Rightarrow {{{S_{ADC}}} \over {{S_{ABD}}}} = {n \over m} \cr
& \Rightarrow {{{S_{ADC}}} \over {{S_{ABD}}}} + 1 = {n \over m} + 1 \cr
& \Rightarrow {{{S_{ADC}} + {S_{ABD}}} \over {{S_{ABD}}}} = {{n + m} \over m} \cr} \)
\( \Rightarrow \dfrac{S_{ABD}}{S_{ADC}+S_{ABD}}= \dfrac{m}{n+m}\)
hay \(\dfrac{S_{ABD}}{S_{ABC}}= \dfrac{m}{n+m}\)
\( \Rightarrow {S_{AB{\rm{D}}}} = \dfrac{{mS}}{{n + m}}\)
Vì \(AM\) là trung tuyến của \(∆ABC\) (gt) \(\Rightarrow S_{ABM}= \dfrac{1}{2}S_{ABC}\).
Có \(AB < AC( m<n)\) vì \(AD\) là đường phân giác, \(AM\) là đường trung tuyến kẻ từ \(A\) nên \(AD\) nằm giữa \(AB\) và \(AM\).
\( \Rightarrow S_{ADM}= S_{ABM}- S_{ABD}\)
\( \Rightarrow S_{ADM} = \dfrac{1}{2}S -\dfrac{m}{n+m}S \)\(\,= \dfrac{S(m+n-2m)}{2(m+n)}\)
\(S_{ADM}= \dfrac{S(n -m)}{2(m+n)}\) (với \(n>m\))
b) Khi \(n = 7cm, m = 3cm\) ta có:
\({S_{A{\rm{D}}M}} = \dfrac{{7 - 3}}{{2\left( {7 + 3} \right)}}.S = \dfrac{S}{5} = \dfrac{{20.S }}{100} \)\(\,= 20\% S\)
Vậy \(S_{ADM} = 20\%S_{ABC}\).
8. Giải bài 22 trang 68 SGK Toán 8 tập 2
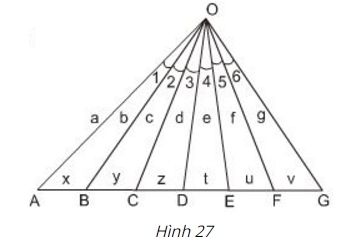
Đố: Hình 27 cho biết có 6 góc bằng nhau:
\(\widehat{O_{1}} = \widehat {O_{2}} = \widehat {O_{3}} \)\(= \widehat {O_{4}} = \widehat {O_{5}} = \widehat {O_{6}}\).
Kích thước các đoạn thẳng đã được ghi trên hình. Hãy thiết lập những tỉ lệ thức từ kích thước đã cho.
Phương pháp giải
Ta có:
\(OB\) là tia phân giác trong của \(∆OAC\) \( \Rightarrow \) \(\dfrac{x}{a} = \dfrac{y}{c}\)
\(OC\) là tia phân giác trong của \(∆OBD\) \(\Rightarrow \) \(\dfrac{y}{b} = \dfrac{z}{d}\)
Thực hiện tương tự với các ta phân giác còn lại: \(OC,OD, OE, OF\)
Hướng dẫn giải
\(OB\) là tia phân giác trong của \(∆OAC\) \( \Rightarrow \) \(\dfrac{x}{a} = \dfrac{y}{c}\)
\(OC\) là tia phân giác trong của \(∆OBD\) \(\Rightarrow \) \(\dfrac{y}{b} = \dfrac{z}{d}\)
\(OD\) là tia phân giác trong của \(∆OCE\) \( \Rightarrow \) \(\dfrac{z}{c}= \dfrac{t}{e}\)
\(OE\) là tia phân giác trong của \(∆ODF\) \( \Rightarrow \) \(\dfrac{t}{d} = \dfrac{u}{f}\)
\(OF\) là tia phân giác trong của \(∆OEG\) \( \Rightarrow \) \(\dfrac{u}{e} = \dfrac{v}{g}\)
\(OC\) là tia phân giác của \(∆AOE\) \( \Rightarrow \) \(\dfrac{AC}{OA} = \dfrac{CE}{OE}\) hay \(\dfrac{x+ y}{a} = \dfrac{z + t}{e}\)
\(OE\) là phân giác của \(∆OCG\) \( \Rightarrow \) \(\dfrac{z + t}{c} = \dfrac{u+v }{g}\)
\(OD\) là phân giác của \(∆AOG\) \( \Rightarrow \) \(\dfrac{x+y+z }{a} = \dfrac{t+u+v }{g}\)
\(OD\) là phân giác của \(∆OBF\) \( \Rightarrow \) \(\dfrac{y+z}{b} = \dfrac{t + u}{f}\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 8 Bài 1: Định lí Ta-lét trong tam giác
- doc Giải bài tập SGK Toán 8 Bài 2: Định lí đảo và hệ quả của định lí Ta-lét
- doc Giải bài tập SGK Toán 8 Bài 4: Khái niệm hai tam giác đồng dạng
- doc Giải bài tập SGK Toán 8 Bài 5: Trường hợp đồng dạng thứ nhất
- doc Giải bài tập SGK Toán 8 Bài 6: Trường hợp đồng dạng thứ hai
- doc Giải bài tập SGK Toán 8 Bài 7: Trường hợp đồng dạng thứ ba
- doc Giải bài tập SGK Toán 8 Bài: Luyện tập 1
- doc Giải bài tập SGK Toán 8 Bài: Luyện tập 2
- doc Giải bài tập SGK Toán 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông
- doc Giải bài tập SGK Toán 8 Bài: Luyện tập
- doc Giải bài tập SGK Toán 8 Bài 9: Ứng dụng thực tế của tam giác đồng dạng
- doc Giải bài tập SGK Toán 8 Ôn tập chương 3: Tam giác đồng dạng