Bài 3: Các tham số đặc trưng của mẫu
Bài giảng Lý thuyết xác suất thống kê Bài 3: Các tham số đặc trưng của mẫu cung cấp các nội dung chính bao gồm trung bình mẫu, phương sai mẫu, độ lệch chuẩn mẫu, tỷ lệ mẫu. Để nắm nội dung chi tiết bài giảng, mời các bạn cùng eLib tham khảo nhé!
Mục lục nội dung

Bài 3: Các tham số đặc trưng của mẫu
Khi nghiên cứu mẫu, người ta thường quan tâm đến các tham số đặc trưng sau đây:
1. Trung bình mẫu
Định nghĩa: Cho mẫu ngẫu nhiên kích thước n, được xây dựng từ đại lượng ngẫu nhiên WX=(X1,X2,...,Xn).
Trung bình mẫu ngẫu nhiên (ký hiệu là ¯X) được định nghĩa:
¯X=1nn∑i=1Xi
Do X1, X2,...Xn là các đại lượng ngẫu nhiên, theo định nghĩa trên thì ¯X là hàm của n đại lượng ngẫu nhiên X1, X2,...Xn nên ¯X cũng là một đại lượng ngẫu nhiên.
Nếu có mẫu cụ thể: WX = (X1, X2,..., Xn) thì ta sẽ tính được giá trị của ¯X (ký hiệu là ¯x).
¯x được tính theo công thức:
¯x=1nn∑i=1xi
Như vậy ¯x là một giá trị của ¯X, đồng thời là trung bình của mẫu cụ thể WX=(X1,X2,...,Xn)
Tính chất: Nếu đại lượng ngẫu nhiên gốc X có kỳ vọng toán: E(X)=μ
và phương sai: Var(X)=σ2
thì: E(¯X)=μ và Var(¯X)=σ2/n
Thật vậy, theo tính chất của kỳ vọng toán, ta có:
E(¯X)=E(1nn∑i=1Xi)=1nn∑i=1E(Xi)=1n.n.μ=μ
Để ý rằng các đại lượng ngẫu nhiên Xi độc lập, có cùng phân phối xác suất với đại lượng ngẫu nhiên gốc X.
Theo tính chất của phương sai thì:
Var(¯X)=Var(1nn∑i=1Xi)=1n2n∑i=1Var(Xi)=1n2.n.σ2=σ2n
Như vậy, bất kể qui luật phân phối xác suất của đại lượng ngẫu nhiên gốc như thế nào, thống kê ¯X cũng có kỳ vọng toán bằng kỳ vọng của đại lượng ngẫu nhiên gốc [E(X)=E(¯X)]. Còn phương sai của ¯X nhỏ hơn phương sai của đại lượng ngẫu nhiên gốc n lần. Nghĩa là các giá trị có thể có của ¯X ổn định quanh kỳ vọng hơn các giá trị có thể có của X.
Nếu lấy căn bậc hai của var(¯X) thì ta sẽ được độ lệch chuẩn σ(ˉX) phản ánh sai số ước lượng do đó người ta thường gọi nó là sai số chuẩn, ký hiệu là se(¯X). Vậy:
se(ˉX)=σ(ˉX)=√var(ˉX)=σ√n
Ở trên ta luôn giả thiết rằng mẫu được rút ra từ tổng thể theo phương thức có hoàn lại. Nếu kích thước tổng thể là vô hạn hoặc kích thước tổng thể là hữu hạn nhưng n > 0,1N thì có thể lấy mẫu không hoàn lại mà không ảnh hưởng đến kết quả. Trường hợp n < 0,1N thì đối với các công thức trên phải sử dụng hệ so điều chỉnh do mẫu là không lặp. Khi đó ta có:
var(¯X)=N−nN−1.σ2n và se(¯X)=√N−nN−1.σ2n
Thí dụ: Xem tổng thể là tập hợp gồm 5 công ty A, B, C, D, E với lợi nhuận (tỷ đồng/năm) lần lượt là: 29, 31, 32, 33, 36. Lấy mẫu ngẫu nhiên kích thước n = 4 từ tổng thể này. Tính kỳ vọng toán và phương sai của trung bình mẫu ngẫu nhiên trong hai trường hợp:
a- Chọn mẫu có lặp; b- Chọn mẫu không lặp.
Giải:
Trường hợp chọn mẫu có lặp:
Gọi X là lợi nhuận của một công ty chọn ngẫu nhiên từ tổng thể gồm 5 công ty A, B, C, D, E. Phân phối xác suất của X như sau:

Từ bảng phân phối xác suất của đại lượng ngẫu nhiên X, ta tính được:
E(X)=0,2(29+31+32+33+36)=32,2
Var(X)=0,2(292+312+322+332+362)−(32,2)2=5,36
Vậy:
E(¯X)=E(X)=32,2;var(¯X)=5,36/4=1,34
Trường hợp chọn mẫu không lặp:
Có C45=5 cách chọn mẫu. Các trường hợp có thể xảy ra, giá trị trung bình mẫu (X) có thể nhận và các xác suất tương ứng được cho ở bảng sau:
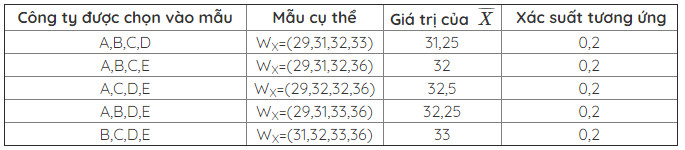
Từ kết quả của bảng trên, ta tính được:
E(¯X)=0,2(31,25+32+32,5+32,25+33)=32,2
Var(¯X)=0,2[(31,25)2+(32)2+(32,5)2+(32,25)2+(33)2]−(32,2)2=0,335
ta cũng có thể tìm được kết quả trên bằng cách áp dụng công thức:
var(¯X)=N−nN−1.σ2n=(5−45−1).5,364=0,335
Phân phối xác suất của ¯X
Phân phối xác suất của trung bình mẫu phụ thuộc vào phân phối xác suất của đại lượng ngẫu nhiên gốc. Người ta đã chứng minh được rằng: Nếu X có
phân phối chuẩn N(μ;σ2) thì ¯X có phân phối chuẩn N(μ;σ2/n)
2. Phương sai mẫu
Định nghĩa: Cho mẫu ngẫu nhiên WX = (X1, X2..... Xn)
Phương sai của nó (ký hiệu là S2) được định nghĩa:
S2=1n−1n∑i=1(Xi−¯X)2
Trong đó ¯X là trung bình của mẫu ngẫu nhiên.
Chú ý: Theo định nghĩa trên, ta thấy phương sai mẫu ngẫu nhiên là hàm của n đại lượng ngẫu nhiên X1, X2, . . . , Xn nên S2 cũng là một đại lượng ngẫu nhiên.
Nếu có mẫu cụ thể: WX = (x1, x2,..., xn) thì S2 sẽ nhận giá trị:
S2=1n−1n∑i=1(xi−¯x)2
s2 gọi là phương sai của mẫu cụ thể.
Tính chất của S2
Do S2 là đại lượng ngẫu nhiên nên ta có thể tính E(S2).
Giả sử: E(X)=μ;Var(X)=σ2
Tacó:
(Xi−¯X)2=[(Xi−μ)−(¯X−μ)]2=(Xi−μ)2−2(¯X−μ).(Xi−μ)+(¯X−μ)2
Do đó:
1nn∑i=1(Xi−¯X)2=1nn∑i=1(Xi−μ)2−2(¯X−μ).1nn∑i=1(Xi−μ)+(¯X−μ)2
Vì: 1nn∑i=1(Xi−μ)=1nn∑i=1Xi−μ=¯X−μ
Nên: 2(¯X−μ).1nn∑i=1(Xi−μ)=2(¯X−μ)2
Do đó:
1nn∑i=1(Xi−¯X)2=1nn∑i=1(Xi−μ)2−(¯X−μ)2
E(S2)=E[1n−1n∑i=1(Xi−¯X)2]=E{nn−1[1n−1n∑i=1(Xi−¯X)2]}
=nn−1E[1nn∑i=1(Xi−μ)2−(¯X−μ)2]
=nn−1{1nn∑i=1E(Xi−μ)2−E[(¯X−μ)2]}
Vì:
E(Xi)=μ(∀i) nên E(Xi−μ)2=Var(Xi)=Var(X)=σ2
E(¯X)=μ nên E[(¯X−μ)2]=Var(¯X)=σ2/n
Do đó:
E(S2)=nn−1(1n.n.σ2−σ2n)=nn−1(n−1nσ2)=σ2
Như vậy, kỳ vọng toán của phương sai mẫu bằng phương sai của đại lượng ngẫu nhiên gốc X.
Định lý 1:
Giả sử X∼N(μ,σ2) và Wx = (X1, X2, .... Xn) là mẫu ngẫu nhiên kích thước n được thành lập từ X. Khi đó:
- n∑i=1(Xi−μ)2σ2∼χ2(n) (n−1)S2σ2∼χ2(n−1)
Định lý 2:
X∼N(μ,σ2) thì ¯X−μS/√n∼T(n−1)
Thí dụ: Quan sát số con ưong một gia đình ở một khu đô thị mới. Gọi X là số con trong một hộ gia đình. Cho biết bảng phân phối xác suất của X như sau:

Từ bảng phân phối xác suất của X ta dễ dàng tính được E(X)=μ=1,3 và Var(X)−σ2=0,61
Gọi Wx = (X1, X2) là mẫu ngẫu nhiên 2 chiều được thành lập từ X. Các đại lượng ngẫu nhiên X1, X2 độc lập, có phân phối xác suất giống X.
Đối với mẫu này, ta có phương sai mẫu:
S2=12−1[(X1−¯X)2+(X2−¯X)2]
Bảng sau đây liệt kê các giá trị của S2 và các xác suất tương ứng.
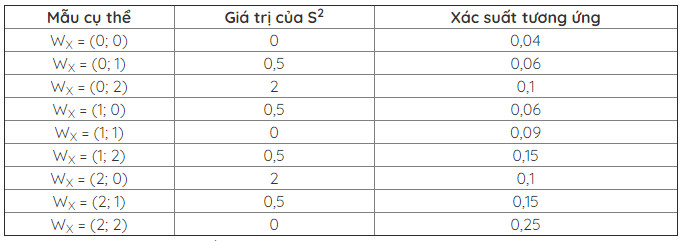
Trong bảng trên, các xác suất tương ứng được tính như sau:
P(X1=0,X2=0)=P(X1=0)P(X2=0)=0,2x0,2=0,04
P(X1=0,X2=1)=P(X1=0)P(X2=1)=0,2x0,3=0,06
....
Bảng phân phối xác suất của S2:

Vậy: E(S2) = 0 x 0,38 + 0,5 x 0,42 + 2 x 0,2 = 0,61 = σ2
3. Độ lệch chuẩn mẫu
Độ lệch chuẩn của mẫu ngẫu nhiên (ký hiệu là S) là căn bậc hai của phương sai mẫu: S=√S2
Nếu có mẫu cụ thể thì độ lệch chuẩn của mẫu cụ thể này là một giá trị của S (ký hiệu là s): s=√s2
4. Tỷ lệ mẫu
Từ một tổng thể gồm N phần tử, trong đó có M phần tử có tính chất A. Ta lấy ngẫu nhiên n phần tử vào mẫu (lấy theo phương thức có hoàn lại). Gọi Xi (i = 1,2, .... n) là số phần tử có tính chất A trong lần lấy phần tử thứ i vào mẫu. Xi (i = 1, 2,..., n) là các đại lượng ngẫu nhiên chỉ có thể nhận một trong hai giá trị: Xi nhận giá trị 0 nếu phần tử thứ i lấy vào mẫu không có tính chất A; Xi nhận giá trị 1 nếu phần tử thứ i lấy vào mẫu có tính chất A.
Tỷ lệ mẫu ngẫu nhiên (ký hiệu F) được định nghĩa như sau:
F=1nn∑i=1Xi
Trong đó nA là tổng số phần tử có tính chất A có trong mẫu cụ thể; n là kích thước mẫu.
Như vậy f là giá trị của F và cũng là tỷ lệ các phần tử có tính chất A của mẫu cụ thể.
Trên đây là nội dung bài giảngBài 3: Các tham số đặc trưng của mẫu mà eLib.VN muốn chia sẻ đến các bạn sinh viên. Hy vọng đây sẽ là tư liệu hữu ích giúp các bạn nắm được nội dung bài học tốt hơn. Chúc các bạn học tốt.
Tham khảo thêm
- doc Bài 1: Tổng thể và mẫu
- doc Bài 2: Mô hình xác suất của tổng thể và mẫu
- doc Bài 4: Phương pháp tính các tham số đặc trưng của mẫu
- doc Bài 5: Mẫu ngẫu nhiên hai chiều




