Giải bài tập SGK Toán 10 Chương 2 Bài 2: Tích vô hướng của hai vectơ
Hướng dẫn Giải bài tập SGK Hình học 10 Bài Tích vô hướng của hai vectơ dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 1 trang 45 SGK Hình học 10
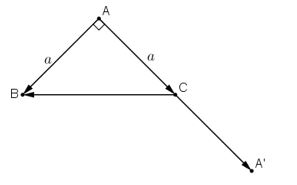
Cho tam giác vuông cân \(ABC\) có \(AB = AC = a\). Tính các tích vô hướng \(\vec{AB}.\vec{AC}\), \(\vec{AC}.\vec{CB}\).
Phương pháp giải
- Hai vectơ vuông góc với nhau thì tích vô hướng của chúng bằng 0.
- Tam giác vuông cân thì có một góc vuông bằng 90 độ, hai góc còn lại mỗi góc bằng 45 độ.
- Tính được cạnh huyền của tam giác bằng định lý Py-ta-go.
- Áp dụng công thức tích vô hướng của vectơ \(\overrightarrow a\) và \( \overrightarrow b \) được xác định bởi công thức sau:
\(\overrightarrow a \overrightarrow {.b} = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right).\)
Hướng dẫn giải
\(\vec{AB} ⊥\vec{AC}\Rightarrow \vec{AB}.\vec{AC} = 0\)
\(\vec{AC}.\vec{CB} =(- \vec{CA}). \vec{CB}=- (\vec{CA}. \vec{CB})\)
Ta có: \(CB= \sqrt{AB^2+AC^2}\)\(=\sqrt{a^2+a^2}=a\sqrt2\) (Định lý Py-ta-go)
Lại có \(\widehat{ACB} = 45^0\) vì \(\Delta ABC\) là tam giác vuông cân tại \(A.\)
Vậy \(\vec{AC}.\vec{CB} = -(\vec{CA}. \vec{CB})\)
\(= -|\vec{CA}|. |\vec{CB}|. \cos\widehat{ACB}\)
\(= - CA. CB .\cos 45^0 \)
\(= - a.a\sqrt 2 .{{\sqrt 2 } \over 2} = - {a^2}.\)
2. Giải bài 2 trang 45 SGK Hình học 10
Cho ba điểm \(O, A, B\) thẳng hàng biết \(OA = a, OB = b\). Tính tích vô hướng của \(\vec{OA}\).\(\vec{OB}\) trong \(2\) trường hợp
a) Điểm \(O\) nằm ngoài đoạn \(AB.\)
b) Điểm \(O\) nằm trong đoạn \(AB.\)
Phương pháp giải
- Hai vectơ cùng phướng thì góc giữa chúng bằng 0 độ.
- Hai vectơ ngược hướng thì góc giữa chúng bằng 180 độ.
- Cho hai vectơ \(\overrightarrow a\) và \( \overrightarrow b \) đều khác vectơ \( \overrightarrow 0. \) Khi đó tích vô hướng của vectlơ \(\overrightarrow a\) và \( \overrightarrow b \) được xác định bởi công thức sau:
\[\overrightarrow a \overrightarrow {.b} = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right).\]
Hướng dẫn giải
Câu a:
Khi \(O\) nằm ngoài đoạn \(AB\) thì hai vec tơ \(\vec{OA}\) và \(\vec{OB}\) cùng hướng.
Do đó góc \((\vec{OA}, \vec{OB}) = 0^0\) \( \Rightarrow \cos(\vec{OA}, \vec{OB}) =\cos 0^0 = 1\)
Nên \(\vec{OA}.\vec{OB} \)
\( = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\)
\(=OA.OB.\cos 0^0 =a.b.1= ab.\)
Câu b:
Khi \(O\) nằm trong đoạn \(AB\) thì hai vec tơ \(\vec{OA}\) và \(\vec{OB}\) ngược hướng.
Do đó góc \((\vec{OA}, \vec{OB}) = 180^0\) \( \Rightarrow \cos(\vec{OA}, \vec{OB}) = \cos 180^0 =-1\)
Nên \(\vec{OA}.\vec{OB} \)
\( = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\)
\(=OA.OB.\cos 180^0 =a.b.(-1)\)\(=- ab.\)
3. Giải bài 3 trang 45 SGK Hình học 10
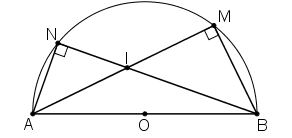
Cho nửa đường tròn tâm \(O\) có đường kính \(AB = 2R\). Gọi \(M\) và \(N\) là hai điểm thuộc nửa đường tròn sao cho hai dây cung \(AM\) và \(BN\) cắt nhau tại \(I\).
a) Chứng minh \(\overrightarrow {AI} .\overrightarrow {AM} = \overrightarrow {AI} .\overrightarrow {AB}\) và \(\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {BI} .\overrightarrow {BA}\);
b) Hãy dùng câu a) để tính \(\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN}\) theo \(R.\)
Phương pháp giải
- Góc nội tiếp chắn nửa đường tròn thì bằng 90 độ.
- Sử dụng quy tắc ba điểm, xen điểm thích hợp.
- Chú ý: \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\)
Hướng dẫn giải
Câu a:
AB là đường kính nên \(\widehat {AMB} = \widehat {ANB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \left\{ \begin{array}{l}
AM \bot MB\\
AN \bot NB
\end{array} \right.\)
Ta có: \({\overrightarrow {AI} .\overrightarrow {AM} } = \overrightarrow {AI} \left( {\overrightarrow {AB} + \overrightarrow {BM} } \right) \)
\(= \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {AI} .\overrightarrow {BM} \)
Mặt khác: \(\overrightarrow {AI} \bot \overrightarrow {BM} \) (do AM\(\bot\) MB) nên \(\overrightarrow {AI} .\overrightarrow {BM} = 0\)
Từ đó: \(\overrightarrow {AI} .\overrightarrow {AM} = \overrightarrow {AI} .\overrightarrow {AB}+0 \) \(= \overrightarrow {AI} .\overrightarrow {AB}\)
Ta có: \(\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {BI} \left( {\overrightarrow {BA} + \overrightarrow {AN} } \right) \)\(= \overrightarrow {BI} .\overrightarrow {BA} + \overrightarrow {BI} .\overrightarrow {AN} \)
Mặt khác: \(\overrightarrow {BI} \bot \overrightarrow {AN} \) (vì BN \(\bot\) NA) nên \(\overrightarrow {BI} .\overrightarrow {AN} = 0\)
Từ đó: \(\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {BI} .\overrightarrow {BA}+0 \)\(=\overrightarrow {BI} .\overrightarrow {BA}\).
Câu b:
\(\eqalign{& \overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN}\cr& = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\overrightarrow {BA} \cr & = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\left( { - \overrightarrow {AB} } \right)\cr & = \overrightarrow {AI} .\overrightarrow {AB} - \overrightarrow {BI} .\overrightarrow {AB} \cr&= \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right) \cr & = \overrightarrow {AB} .\left( {\overrightarrow {AI} + \overrightarrow {IB} } \right)\cr &= \overrightarrow {AB} .\overrightarrow {AB} = {\overrightarrow {AB} ^2} = 4{{\rm{R}}^2} \cr} \)
4. Giải bài 4 trang 45 SGK Hình học 10
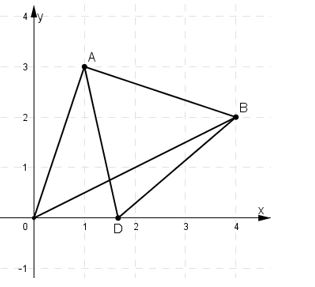
Trên mặt phẳng \(Oxy\), cho hai điểm \(A(1; 3), \, B(4;2)\)
a) Tìm tọa độ điểm \(D\) nằm trên trục \(Ox\) sao cho \(DA = DB\);
b) Tính chu vi tam giác \(OAB\);
c) Chứng tỏ rằng \(OA\) vuông góc với \(AB\) và từ đó tính diện tích tam giác \(OAB.\)
Phương pháp giải
Câu a:
- Điểm \(D \in Ox \Rightarrow D(x_0; \, 0).\)
- \(DA = DB \Leftrightarrow D{A^2} = D{B^2}\)
Câu b:
Chu vi tam giác \(OAB:\;\;\;C = OA + OB + AB.\)
Câu c:
- \(OA \bot AB \Leftrightarrow \overrightarrow {OA} .\overrightarrow {AB} = 0.\)
- \( {S_{OAB}} = \frac{1}{2}OA.AB.\)
Hướng dẫn giải
Câu a:
\(D\) nằm trên trục \(Ox\) nên tọa độ của \(D\) là \((x; 0)\).
Ta có : \(\overrightarrow {DA} = \left( {{x_A} - {x_D};{y_A} - {y_D}} \right) = \left( {1 - x;3} \right)\)
\(\overrightarrow {DB} = \left( {{x_B} - {x_D};{y_B} - {y_D}} \right) = \left( {4 - x;2} \right).\)
\(\Rightarrow DA = \sqrt {{{\left( {1 - x} \right)}^2} + {3^2}} ,\) \(DB = \sqrt {{{\left( {4 - x} \right)}^2} + {2^2}} \)
\(\begin{array}{l}
DA = DB\\
\Leftrightarrow \sqrt {9 + {{\left( {x - 1} \right)}^2}} = \sqrt {{{\left( {x - 4} \right)}^2} + 4} \\
\Leftrightarrow 9 + {\left( {x - 1} \right)^2} = 4 + {\left( {x - 4} \right)^2}\\
\Leftrightarrow {x^2} - 2x + 10 = {x^2} - 8x + 20\\
\Leftrightarrow 6x = 10\\
\Leftrightarrow x = \frac{5}{3}
\end{array}\)
Câu b:
\(\begin{array}{l}
\overrightarrow {OA} = \left( {1;3} \right)\\
\Rightarrow OA = \sqrt {{1^2} + {3^2}} = \sqrt {10} \\
\overrightarrow {OB} = \left( {4;2} \right)\\
\Rightarrow OB = \sqrt {{4^2} + {2^2}} = \sqrt {20} = 2\sqrt 5 \\
\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\\
= \left( {4 - 1;2 - 3} \right) = \left( {3; - 1} \right)\\
\Rightarrow AB = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} \\
\Rightarrow C = OA + AB + OB\\
= \sqrt {10} + \sqrt {10} + 2\sqrt 5 \\
= 2\sqrt {10} + 2\sqrt 5
\end{array}\)
Vậy chu vi tam giác là \(2\sqrt {10} + 2\sqrt 5 \).
Câu c:
Ta có \(\vec{OA}= (1; 3)\); \(\vec{AB} = (3; -1)\)
\(\vec{OA} .\vec{AB} = 1.3 + 3.(-1) = 0 \)
\(\Rightarrow \vec{OA}\) ⊥ \(\vec{AB}\)
Do đó OA\(\bot\)AB nên \(\widehat {OAB} = {90^0}\) hay tam giác OAB vuông tại A.
\({S_{OAB}} = \frac{1}{2}OA.AB\) \( =\frac{1}{2}.\sqrt{10}.\sqrt{10}\)\( =5\) (đvdt)
5. Giải bài 5 trang 45 SGK Hình học 10
Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) trong các trường hợp sau:
a) \(\overrightarrow a = (2; -3) ,\) \(\overrightarrow b = (6, 4);\)
b) \(\overrightarrow a = (3; 2),\) \(\overrightarrow b = (5, -1);\)
c) \(\overrightarrow a = (-2; -2\sqrt3)\), \(\overrightarrow b = (3; \sqrt3)\);
Phương pháp giải
Áp dụng công thức: \(\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right) = \dfrac{{ {\overrightarrow a .\overrightarrow b } }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)\( = \dfrac{{{{x_1}{x_2} + y{ _1}{y_2}} }}{{\sqrt {x_1^2 + y_1^2} .\sqrt {x_2^2 + y_2^2} }}.\)
Hướng dẫn giải
Câu a:
\(\overrightarrow a .\overrightarrow b = 2.6 + \left( { - 3} \right).4 = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b\) hay \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {90^0}\)
Cách trình bày khác:
\(\begin{array}{l}
\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{2.6 + \left( { - 3} \right).4}}{{\sqrt {{2^2} + {{\left( { - 3} \right)}^2}} .\sqrt {{6^2} + {4^2}} }}\\
= \frac{0}{{\sqrt {13} .\sqrt {52} }} = 0\\
\Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {90^0}
\end{array}\)
Câu b:
\(\begin{array}{l}
\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{3.5 + 2.\left( { - 1} \right)}}{{\sqrt {{3^2} + {2^2}} .\sqrt {{5^2} + {{\left( { - 1} \right)}^2}} }}\\
= \frac{{13}}{{\sqrt {13} .\sqrt {26} }} = \frac{1}{{\sqrt 2 }}\\
\Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {45^0}
\end{array}\)
Câu c:
\(\begin{array}{l}
\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \\= \frac{{ - 2.3 + \left( { - 2\sqrt 3 } \right).\sqrt 3 }}{{\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 2\sqrt 3 } \right)}^2}} .\sqrt {{3^2} + {{\left( {\sqrt 3 } \right)}^2}} }}\\
= \frac{{ - 12}}{{\sqrt {16} .\sqrt {12} }} = - \frac{{\sqrt 3 }}{2}\\
\Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {150^0}
\end{array}\)
6. Giải bài 6 trang 46 SGK Hình học 10
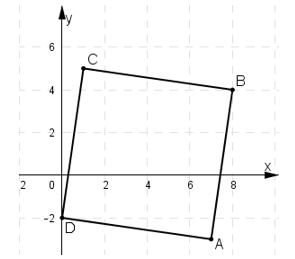
Trên mặt phẳng tọa độ \(Oxy\) cho bốn điểm: \(A(7; -3); B(8; 4); C(1; 5); D(0;-2)\).
Chứng minh rằng tứ giác \(ABCD\) là hình vuông.
Phương pháp giải
- \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow \left\{ \begin{array}{l} AB//DC\\ AB = DC \end{array} \right.\) \( \Rightarrow ABCD\) là hình bình hành.
- \(\overrightarrow {AB} .\overrightarrow {AD} = 0 \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow ABCD\) là hình chữ nhật.
- \(AB = AD \Rightarrow ABCD\)là hình vuông.
Hướng dẫn giải
Ta có: \(\vec{AB} = (1; 7)\); \(\vec{DC}= (1; 7)\), \(\vec{AD} = (-7; 1)\)
\(\Rightarrow \vec{AB} = \vec{DC}\)
Mà \(\overrightarrow {AB} ,\overrightarrow {AD} \) không cùng phương
\(\Rightarrow ABCD\) là hình bình hành (1)
Ta có:
\(\begin{array}{l}
AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{1^2} + {7^2}} \\
= \sqrt {50} = 5\sqrt 2 \\
AD = \left| {\overrightarrow {AD} } \right| = \sqrt {{{\left( { - 7} \right)}^2} + {1^2}} \\
= \sqrt {50} = 5\sqrt 2
\end{array}\)
Suy ra \(AB = AD\), kết hợp với (1) suy ra \(ABCD\) là hình thoi (2)
Mặt khác \(\vec{AB} = (1; 7)\); \(\vec{AD} = (-7; 1)\)
\(\overrightarrow {AB} .\overrightarrow {AD} = 1.( - 7) + 7.1 = 0\)
\( \Rightarrow \vec{AB}⊥\vec{AD}\) nên \(AB\bot AD\) (3)
Kết hợp (2) và (3) suy ra \(ABCD\) là hình vuông.
Chú ý:
Các em cũng có thể đổi thứ thự chứng minh \(AB\bot AD\) lên trước suy ra HCN, rồi mới chứng minh AB=AD suy ra hình vuông cũng được.
7. Giải bài 7 trang 46 SGK Hình học 10
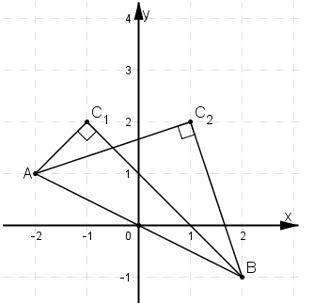
Trên mặt phẳng \(Oxy\) cho điểm \(A(-2; 1)\). Gọi \(B\) là điểm đối xứng với điểm \(A\) qua gốc tọa độ \(O\). Tìm tọa độ của điểm \(C\) có tung độ bằng \(2\) sao cho tam giác \(ABC\) vuông ở \(C\).
Phương pháp giải
- \(B\) là điểm đối xứng với \(A(a; \, b)\) qua gốc tọa độ \( \Rightarrow B\left( { - a; - b} \right).\)
- Tam giác \(ABC\) vuông tại \( C \Leftrightarrow \overrightarrow {CA} \bot \overrightarrow {CB} \Leftrightarrow \overrightarrow {CA} .\overrightarrow {CB} = 0. \)
Hướng dẫn giải
Điểm \(B\) đối xứng với \(A\) qua gốc tọa độ O
\( \Rightarrow \left\{ \begin{array}{l}
{x_B} = - {x_A} = - \left( { - 2} \right) = 2\\
{y_B} = - {y_A} = - 1
\end{array} \right. \) \(\Rightarrow B\left( {2; - 1} \right)\)
C có tung độ bằng 2 nên tọa độ của \(C\) là \((x; 2)\).
Ta có: \(\vec{CA} = (-2 - x; -1)\), \(\vec{CB} = (2 - x; -3)\)
Tam giác \(ABC\) vuông tại \(C\) \( \Leftrightarrow CA \bot CB\)
\(\Rightarrow\vec{CA} ⊥ \vec{CB}\Rightarrow \vec{CA}.\vec{CB} = 0\)
\(\Rightarrow(-2 - x)(2 - x) + (-1)(-3) = 0\)
\(\Rightarrow -4 +x^2+ 3 = 0\)
\(\Rightarrow x^2= 1 \Rightarrow x= 1\) hoặc \(x= -1\)
Ta tìm được hai điểm \(C_1(1; 2); C_2(-1; 2)\) thỏa mãn yêu cầu bài toán.
Tham khảo thêm
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 1: Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- doc Giải bài tập SGK Toán 10 Ôn tập chương 2: Tích vô hướng của hai vectơ và ứng dụng