Giải bài tập SGK Toán 10 Ôn tập chương 3: Phương pháp tọa độ trong mặt phẳng
Hướng dẫn Giải bài tập SGK Hình học 10 Bài Ôn tập chương 3: Phương pháp tọa độ trong mặt phẳng sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung
1.1. Giải bài 1 trang 93 SGK Hình học 10
1.2. Giải bài 2 trang 93 SGK Hình học 10
1.3. Giải bài 3 trang 93 SGK Hình học 10
1.4. Giải bài 4 trang 93 SGK Hình học 10
1.5. Giải bài 5 trang 93 SGK Hình học 10
1.6. Giải bài 6 trang 93 SGK Hình học 10
1.7. Giải bài 7 trang 93 SGK Hình học 10
1.8. Giải bài 8 trang 93 SGK Hình học 10
1.9. Giải bài 9 trang 93 SGK Hình học 10
1.10. Giải bài 10 trang 94 SGK Hình học 10
2.1. Giải bài 1 trang 94 SGK Hình học 10
2.2. Giải bài 2 trang 94 SGK Hình học 10
2.3. Giải bài 3 trang 94 SGK Hình học 10
2.4. Giải bài 4 trang 94 SGK Hình học 10
2.5. Giải bài 5 trang 94 SGK Hình học 10
2.6. Giải bài 6 trang 95 SGK Hình học 10
2.7. Giải bài 7 trang 95 SGK Hình học 10
2.8. Giải bài 8 trang 95 SGK Hình học 10
2.9. Giải bài 9 trang 95 SGK Hình học 10
2.10. Giải bài 10 trang 95 SGK Hình học 10
2.11. Giải bài 11 trang 95 SGK Hình học 10
2.12. Giải bài 12 trang 95 SGK Hình học 10
2.13. Giải bài 13 trang 95 SGK Hình học 10
2.14. Giải bài 14 trang 96 SGK Hình học 10
2.15. Giải bài 15 trang 96 SGK Hình học 10
2.16. Giải bài 16 trang 96 SGK Hình học 10
2.17. Giải bài 17 trang 96 SGK Hình học 10
2.18. Giải bài 18 trang 96 SGK Hình học 10
2.19. Giải bài 19 trang 96 SGK Hình học 10
2.20. Giải bài 20 trang 96 SGK Hình học 10
2.21. Giải bài 21 trang 96 SGK Hình học 10
2.22. Giải bài 22 trang 97 SGK Hình học 10
2.23. Giải bài 23 trang 97 SGK Hình học 10
2.24. Giải bài 24 trang 97 SGK Hình học 10
2.25. Giải bài 25 trang 97 SGK Hình học 10
2.26. Giải bài 26 trang 97 SGK Hình học 10
2.27. Giải bài 27 trang 98 SGK Hình học 10
2.28. Giải bài 28 trang 98 SGK Hình học 10

1. Câu hỏi và bài tập
1.1. Giải bài 1 trang 93 SGK Hình học 10
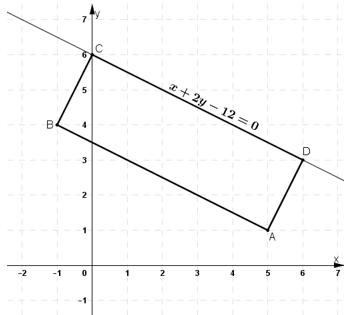
Cho hình chữ nhật \(ABCD\). Biết các đỉnh \(A(5; 1), C(0; 6)\) và phương trình \(CD: x + 2y – 12 = 0.\)
Tìm phương trình các đường thẳng chứa các cạnh còn lại.
Phương pháp giải
- Các cạnh của hình chữ nật vuông góc với nhau nên ta có thể suy ra được VTPT của đường thẳng chứa các cạnh còn lại của hình chữ nhật từ đường thẳng CD.
- Phương trình đường thẳng đi qua điểm \(M(x_0;y_0)\) có VTPT \(\overrightarrow n \left( {a;b} \right)\) là:
\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)
Hướng dẫn giải
Viết phương trình \(AB\).
\(CD\) có VTPT \(\overrightarrow {{n_1}} = \left( {1;2} \right)\).
\(AB//CD\) nên có VTPT \(\overrightarrow {{n_1}} = \left( {1;2} \right)\)
Mà \(AB\) đi qua \(A\left( {5;1} \right)\) nên \(AB:1\left( {x - 5} \right) + 2\left( {y - 1} \right) = 0\) hay \(x + 2y - 7 = 0\).
Viết phương trình \(AD\).
\(CD\) có VTPT \(\overrightarrow {{n_1}} = \left( {1;2} \right)\) nên có VTCP \(\overrightarrow {{u_1}} = \left( {2; - 1} \right)\).
\(AD \bot CD\) nên nhận \(\overrightarrow {{n_2}} = \overrightarrow {{u_1}} = \left( {2; - 1} \right)\) làm VTPT
Mà \(AD\) đi qua \(A\left( {5;1} \right)\) nên \(AD:2\left( {x - 5} \right) - 1.\left( {y - 1} \right) = 0\) hay \(2x - y - 9 = 0\).
Viết phương trình \(BC\).
\(BC \bot CD\) nên nhận \(\overrightarrow {{n_2}} = \overrightarrow {{u_1}} = \left( {2; - 1} \right)\) làm VTPT.
Mà \(BC\) đi qua \(C\left( {0;6} \right)\) nên \(BC:2\left( {x - 0} \right) - 1\left( {y - 6} \right) = 0\) hay \(2x - y + 6 = 0\).
Vậy \(AB: x +2 y – 7 = 0\)
\(BC : 2x - y + 6 = 0\)
\(AD : 2x – y – 9 = 0\)
1.2. Giải bài 2 trang 93 SGK Hình học 10
Cho \(A(1; 2), \, \, B(-3; 1)\) và \(C(4; -2)\). Tìm tập hợp điểm \(M\) sao cho \(M{A^2} + M{B^2} = M{C^2}\)
Phương pháp giải
- Gọi \((x; y)\) là tọa độ của điểm \(M\).
- Tính \(AM^2,BM^2,CM^2\) rồi thay vào đẳng thức đã cho tìm mối quan hệ x,y.
Hướng dẫn giải
Gọi \((x; y)\) là tọa độ của điểm \(M\).
\(\begin{array}{l}
AM = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y - 2} \right)}^2}} \\
\Rightarrow A{M^2} = {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2}\\
= {x^2} - 2x + 1 + {y^2} - 4y + 4\\
= {x^2} + {y^2} - 2x - 4y + 5\\
BM = \sqrt {{{\left( {x + 3} \right)}^2} + {{\left( {y - 1} \right)}^2}} \\
\Rightarrow B{M^2} = {\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2}\\
= {x^2} + 6x + 9 + {y^2} - 2y + 1\\
= {x^2} + {y^2} + 6x - 2y + 10\\
CM = \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y + 2} \right)}^2}} \\
\Rightarrow C{M^2} = {\left( {x - 4} \right)^2} + {\left( {y + 2} \right)^2}\\
= {x^2} - 8x + 16 + {y^2} + 4y + 4\\
= {x^2} + {y^2} - 8x + 4y + 20
\end{array}\)
Theo giả thiết, ta có: \(M{A^2} + M{B^2} = M{C^2}\)
\(\begin{array}{l}
\Leftrightarrow A{M^2} + B{M^2} = C{M^2}\\
\Leftrightarrow \left( {{x^2} + {y^2} - 2x - 4y + 5} \right)\\
\,\, + \left( {{x^2} + {y^2} + 6x - 2y + 10} \right)\\
\,\, = {x^2} + {y^2} - 8x + 4y + 20\\
\Leftrightarrow (2{x^2} + 2{y^2} + 4x - 6y + 15)\\
- \left( {{x^2} + {y^2} - 8x + 4y + 20} \right) = 0\\
\Leftrightarrow {x^2} + {y^2} + 12x - 10y - 5 = 0\\
\Leftrightarrow \left( {{x^2} + 12x + 36} \right) + \left( {{y^2} - 10y + 25} \right) - 66 = 0\\
\Leftrightarrow {\left( {x + 6} \right)^2} + {\left( {y - 5} \right)^2} = 66
\end{array}\)
Vậy quỹ tích các điểm \(M\) thỏa mãn đẳng thức \(M{A^2} + M{B^2} = M{C^2}\) là đường tròn tâm \(I (-6; 5)\) và bán kính \(R = \sqrt{66}\).
1.3. Giải bài 3 trang 93 SGK Hình học 10
Tìm tập hợp các điểm cách đều hai đường thẳng: \({\Delta _1} : 5x + 3y – 3 = 0\) và \({\Delta _2}: 5x + 3y + 7 = 0.\)
Phương pháp giải
Sử dụng công thức tính khoảng cách từ điểm đến đường thẳng:
\(d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Hướng dẫn giải
Gọi \(M(x; y)\) là một điểm bất kì trong mặt phẳng, ta có:
\(d(M,{\Delta _1}) = {{|5x + 3y - 3|} \over {\sqrt {{5^2} + {3^2}} }} = {{|5x + 3y - 3|} \over {\sqrt {34} }}\)
\(d(M,{\Delta _2}) = {{|5x + 3y + 7|} \over {\sqrt {{5^2} + {3^2}} }} = {{|5x + 3y + 7|} \over {\sqrt {34} }}\)
Điểm \(M\) cách đều hai đường thẳng \({\Delta _1},{\Delta _2}\) nên:
\(\eqalign{
& {{|5x + 3y - 3|} \over {\sqrt {34} }} = {{|5x + 3y + 7|} \over {\sqrt {34} }} \cr
& \Leftrightarrow |5x + 3y - 3| = |5x + 3y + 7| \cr} \)
Ta xét hai trường hợp:
\(5x + 3y – 3 = - (5x + 3y + 7)\)
\(\begin{array}{l}
\Leftrightarrow 5x + 3y - 3 = - 5x - 3y - 7\\
\Leftrightarrow 10x + 6y + 4 = 0\\
\Leftrightarrow 5x + 3y + 2 = 0
\end{array}\)
\(5x + 3y – 3 = 5x + 3y + 7\)
\( \Leftrightarrow 0x + 0y - 10 = 0\) (vô nghiệm)
Vậy tập hợp các điểm \(M\) cách đều hai đường thẳng \({\Delta _1},{\Delta _2}\) là đường thẳng \(Δ: 5x + 3y + 2 = 0\)
Dễ thấy \(Δ\) song song với \({\Delta _1},{\Delta _2}\) và hai đường thẳng \({\Delta _1},{\Delta _2}\) nằm về hai phía đối với \(Δ\).
1.4. Giải bài 4 trang 93 SGK Hình học 10
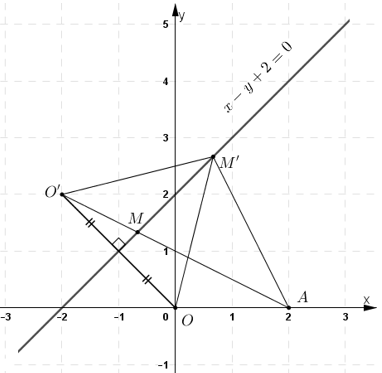
Cho đường thẳng \(Δ: x – y + 2=0\) và hai điểm \(O(0; 0); \, A(2; 0).\)
a) Tìm điểm đối xứng của \(O\) qua \(Δ\)
b) Tìm điểm \(M\) trên \(Δ\) sao cho độ dài đường gấp khúc \(OMA\) ngắn nhất.
Phương pháp giải
a) Tìm hình chiếu H của O trên Δ; rồi tìm điểm O' là hình chiếu của O qua Δ khi H là trung điểm của OO'.
b) Độ dài đường gấp khúc \(OMA\) ngắn nhất khi M là giao điểm của Δ và đường trung trực của OO'.
Hướng dẫn giải
Câu a:
Gọi \(H(x;y)\) là hình chiếu của \(O\) trên \(Δ\), \(\overrightarrow {OH} = (x;y)\)
\( Δ: x – y + 2 = 0\) có vecto chỉ phương \(\overrightarrow u (1;1)\)
\(\overrightarrow {OH} \bot \Delta \) \(\Rightarrow 1.x + 1.y = 0 \Leftrightarrow x + y = 0\)
Tọa độ điểm \(H\) là nghiệm của hệ phương trình:
\(\left\{ \matrix{
x + y = 0 \hfill \cr
x - y + 2 = 0 \hfill \cr} \right. \Rightarrow H( - 1;1)\)
Gọi \(O’\) là đỉnh đối xứng của \(O\) qua \(Δ\) thì \(H\) là trung điểm của đoạn thẳng \(OO’\)
\(\eqalign{
& {x_H} = {{{x_O} + {x_{O'}}} \over 2} \Leftrightarrow - 1 = {{0 + {x_{O'}}} \over 2} \cr&\Rightarrow {x_{O'}} = - 2 \cr
& {y_H} = {{{y_O} + {y_{O'}}} \over 2} \Leftrightarrow - 1 = {{0 + {y_{O'}}} \over 2}\cr& \Rightarrow {y_{O'}} = 2 \cr} \)
Vậy \(O’(-2;2)\).
Câu b:
Quan sát hình vẽ ta thấy,
\(A\) và \(O\) nằm cùng phía so với \(\Delta \) hay \(A,O'\) nằm khác phía so với \(\Delta \).
Gọi \(M' = AO' \cap \Delta \) thì \(OM' = O'M'\) do \(\Delta \) là đường trung trực của \(OO'\).
Với điểm \(M\) bất kì thuộc \(\Delta \) thì \(OM + AM = O'M + AM \ge O'A\)
\( \Rightarrow {\left( {OM + MA} \right)_{\min }} = AO'\) khi \(M \equiv M'\) là giao điểm của \(AO'\) với \(\Delta \).
\(A(2; 0); O'(-2; 2)\) \( \Rightarrow \overrightarrow {AO'} = \left( { - 4;2} \right)\) là VTCP của \(AO'\) \( \Rightarrow \overrightarrow {{n_{AO'}}} = \left( {2;4} \right)\) là VTPT của \(AO'\)
Mà \(AO'\) đi qua \(A\left( {2;0} \right)\) nên \(2\left( {x - 2} \right) + 4\left( {y - 0} \right) = 0\) \( \Leftrightarrow 2x + 4y - 4 = 0\) \( \Leftrightarrow x + 2y - 2 = 0\)
\(M = AO' \cap \Delta \) \( \Leftrightarrow \left\{ \begin{array}{l}x + 2y - 2 = 0\\x - y + 2 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{2}{3}\\y = \dfrac{4}{3}\end{array} \right.\)
Vậy \(M\left( { - \dfrac{2}{3};\dfrac{4}{3}} \right)\)
1.5. Giải bài 5 trang 93 SGK Hình học 10
Cho ba điểm A(4; 3), B(2; 7) và C(-3; -8).
a) Tìm tọa độ trọng tâm G và trực tâm H của tam giác ABC;
b) Gọi T là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh T, G và H thẳng hàng.
c) Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Phương pháp giải
Sử dụng công thức trọng tâm tìm \(G\).
Sử dụng tính chất \(\overrightarrow {AH} .\overrightarrow {BC} = 0\) và \(\overrightarrow {BH} .\overrightarrow {AC} = 0\) tìm tọa độ điểm \(H\).
\(T\) là tâm đường tròn ngoại tiếp thì \(TA=TB=TC\).
Hướng dẫn giải
Câu a:
Gọi \(G(x_G; \, y_G)\) là trọng tâm tam giác \(\Delta ABC.\) Khi đó ta có:
\(\eqalign{
& {x_G} = {{{x_A} + {x_B} + {x_C}} \over 3}\cr& \Rightarrow {x_G} = {{4 + 2 - 3} \over 3} = 1 \cr
& {y_G} = {{{y_A} + {y_B} + {y_C}} \over 3}\cr& \Rightarrow {y_G} = {{3 + 7 - 8} \over 3} = {2 \over 3} \cr} \)
Vậy \(G\left(1; \, \, {2 \over 3}\right)\)
Gọi \((x; y)\) là tọa độ của \(H\)
\(\eqalign{
& \overrightarrow {AH} = (x - 4; \, y - 3);\cr&\overrightarrow {BC} = ( - 5; \, - 15) \cr
& \overrightarrow {BH} = (x - 2; \, y - 7);\cr&\overrightarrow {AC} = ( - 7; \, - 11) \cr
& \overrightarrow {AH} \bot \overrightarrow {BC}\cr& \Leftrightarrow \overrightarrow {AH} .\overrightarrow {BC} = 0 \cr
& \Leftrightarrow - 5(x - 4) - 15(y - 3) = 0 \cr&\Leftrightarrow x + 3y - 13 = 0 \cr
& \overrightarrow {BH} \bot \overrightarrow {AC} \cr&\Leftrightarrow \overrightarrow {BH} .\overrightarrow {AC} = 0 \cr
& \Leftrightarrow - 7(x - 2) - 11(y - 7) = 0 \cr&\Leftrightarrow 7x + 11y - 91 = 0 \cr} \)
Tọa độ điểm \(H\) là nghiệm của hệ phương trình:
\(\left\{ \matrix{
x +3 y - 13 = 0 \hfill \cr
7x + 11y - 91 = 0 \hfill \cr} \right. \Rightarrow H(13;0)\)
Câu b:
Tâm \(T\) của đường tròn ngoại tiếp tam giác \(ABC\) thỏa mãn điều kiện
\(TA = TB = TC \)\(⇒ TA^2= TB^2= TC^2\)
\(⇒ {\left( {x{\rm{ }}-{\rm{ }}4} \right)^2} +{\left( {y-3} \right)^2} \)\(= {\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}2} \right)^2} + {\left( {y{\rm{ }}-{\rm{ }}7} \right)^2}\)
\( \Leftrightarrow {x^2} - 8x + 16 + {y^2} - 6y + 9\) \(= {x^2} - 4x + 4 + {y^2} - 14y + 49\)
\( \Leftrightarrow - 4x + 8y - 28 = 0\)
\( \Leftrightarrow {\rm{ }}x{\rm{ }}-{\rm{ }}2y{\rm{ }} + {\rm{ }}7 =0\)
\({\left( {x{\rm{ }}-{\rm{ }}4} \right)^2} +{\left( {y-3} \right)^2} \)\(= {\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}3} \right)^2} + {\rm{ }}{\left( {y +8} \right)^2}\)
\(\Leftrightarrow {x^2} - 8x + 16 + {y^2} - 6y + 9 \) \(= {x^2} + 6x + 9 + {y^2} + 16y + 64\)
\( \Leftrightarrow - 14x - 22y - 48 = 0\)
\( \Leftrightarrow {\rm{ }}7x{\rm{ }} + 11y +24 = 0\)
Do đó tọa độ tâm \(T\) của đường tròn ngoại tiếp tam giác \(ABC\) là nghiệm của hệ:
\(\left\{ \matrix{
x - 2y + 7 = 0 \hfill \cr
7x + 11y + 24 = 0 \hfill \cr} \right. \Rightarrow T( - 5;1)\)
Ta có: \(\overrightarrow {TH} = ( 18;-1);\overrightarrow {TG} = \left( {6; - \dfrac{1}{3}} \right)\)
Ta có: \(\overrightarrow {TH} = {3}\overrightarrow {TG} \)
Vậy ba điểm \(H, G, T\) thẳng hàng.
Câu c:
Đường tròn ngoại tiếp tam giác \(ABC\) có tâm \(T(-5; 1)\), bán kính \(R = AT\)
\({R^2} = A{T^2} = {\left( { - 5-{\rm{ }}4} \right)^2} + {\rm{ }}{\left( {1-3} \right)^2} \)\(= 85\)
Vậy phương trình đường tròn ngoại tiếp tam giác \(ABC\) là:
\((x + 5)^2+ (y – 1)^2= 85\)
1.6. Giải bài 6 trang 93 SGK Hình học 10
Lập phương trình hai đường phân giác của các góc tạo bởi đường thẳng \(3x – 4y + 12 = 0\) và \(12x+5y-7 = 0.\)
Phương pháp giải
Gọi \(\displaystyle M(x; y)\) thuộc đường phân giác của góc tạo bởi đường thẳng.
\(\displaystyle M\) thuộc đường phân giác của góc tạo bởi hai đường thẳng \(\displaystyle d_1\) và \(\displaystyle d_2\) nên cách đều hai đường thẳng đó.
Từ đố lập phương trình đường phân giác cần tìm.
Hướng dẫn giải
Gọi \(\displaystyle M(x; y)\) thuộc đường phân giác của góc tạo bởi đường thẳng trên.
Khi đó, khoảng cách từ \(\displaystyle M\) đến \(\displaystyle d_1 : 3x - 4y + 12 = 0\) là:
\(\displaystyle d(M,{d_1}) = {{|3x - 4y + 12|} \over {\sqrt {9 + 16} }} \) \(\displaystyle = {{|3x - 4y + 12|} \over 5}\)
Khoảng cách từ \(\displaystyle M\) đến \(\displaystyle d_2: 12x + 15y – 7 = 0\) là:
\(\displaystyle d(M,{d_2}) = {{|12x + 5y - 7|} \over {\sqrt {144 + 25} }} \) \(\displaystyle = {{|12x + 5y - 7|} \over {13}}\)
Ta có: \(\displaystyle M\) thuộc đường phân giác của góc tạo bởi hai đường thẳng \(\displaystyle d_1\) và \(\displaystyle d_2\) nên cách đều hai đường thẳng đó.
Suy ra:
\(\displaystyle \eqalign{
& d(M,{d_1}) = d(M,{d_2})\cr& \Leftrightarrow {{|3x - 4y + 12|} \over 5} = {{|12x + 5y - 7|} \over {13}} \cr
& \Leftrightarrow \left[ \matrix{
{{3x - 4y + 12} \over 5} = {{12x + 5y - 7} \over {13}} \hfill \cr
{{3x - 4y + 12} \over 5} = - {{12x + 5y - 7} \over {13}} \hfill \cr} \right.\cr} \)
\(\begin{array}{l}
\Leftrightarrow \left[ \begin{array}{l}
13\left( {3x - 4y + 12} \right) = 5\left( {12x + 5y - 7} \right)\\
13\left( {3x - 4y + 12} \right) = - 5\left( {12x + 5y - 7} \right)
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
39x - 52y + 156 = 60x + 25y - 35\\
39x - 52y + 156 = - 60x - 25y + 35
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
21x + 77y - 191 = 0\\
99x - 27y + 121 = 0
\end{array} \right.
\end{array}\)
Vậy ta có phương trình của hai đường phân giác của các góc tạo bởi \(\displaystyle d_1\) và \(\displaystyle d_2\) là:
\(\displaystyle \Delta _1: 21x + 77y – 191 = 0\)
\(\displaystyle \Delta _2: 99x – 27y + 121 = 0\)
1.7. Giải bài 7 trang 93 SGK Hình học 10
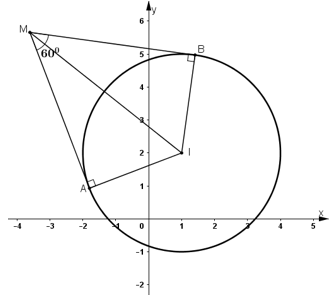
Cho đường tròn \((C)\) có tâm \(I(1; 2)\) và bán kính bằng \(3\). Chứng minh rằng tập hợp các điểm \(M\) từ đó ta sẽ được hai tiếp tuyến với \((C)\) tạo với nhau một góc \(60^0\) là một đường tròn. Hãy viết phương trình đường tròn đó.
Phương pháp giải
Tính khoảng cách MI dựa vào tỉ số lượng giác của góc nhọn trong tam giác AMI.
Từ đó suy ra quỹ tích cần tìm.
Hướng dẫn giải
Theo tính chất của tiếp tuyến cắt nhau ta có \(\displaystyle MI\) là tia phân giác góc \(\displaystyle M\)
\(\displaystyle \Rightarrow \) \(\displaystyle \widehat {AMI} = {30^0}\)
Tam giác \(\displaystyle IAM\) vuông tại \(\displaystyle A\) (vì \(IA \bot MA\)) có:
\(\displaystyle \sin \widehat {AMI} = \frac{{IA}}{{IM}} \Rightarrow IM = {{IA} \over {\sin \widehat {AMI}}} \) \(\displaystyle = {3 \over {\sin {{30}^0}}} = {3 \over {{1 \over 2}}} = 6\)
\(\displaystyle \Rightarrow \) \(\displaystyle M\) luôn cách \(\displaystyle I\) cố định một khoảng bằng \(\displaystyle 6\).
Vậy quỹ tích \(\displaystyle M\) là đường tròn tâm \(\displaystyle I (1; 2)\), bán kính \(\displaystyle R = 6\)
Phương trình đường tròn là: \(\displaystyle {(x - 1)^2} + {(y - 2)^2} = 36\).
1.8. Giải bài 8 trang 93 SGK Hình học 10
Tìm góc giữa hai đường thẳng \(\Delta_1\) và \(\Delta_2\) trong các trường hợp sau:
a) \(\Delta_1\): \(2x + y – 4 = 0\) ; \(\Delta_2\): \(5x – 2y + 3 = 0.\)
b) \(\Delta_1\): \(y = -2x + 4\); \({\Delta _2}:y = {1 \over 2}x + {3 \over 2}.\)
Phương pháp giải
Cho hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) có VTPT \(\overrightarrow {{n_1}} = \left( {{a_1};{b_1}} \right)\);
\({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) có VTPT \(\overrightarrow {{n_2}} = \left( {{a_2};{b_2}} \right)\).
Gọi \(\alpha \) là góc tạo bởi giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\).
Khi đó
\(\cos \alpha = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \dfrac{{\left| {\overrightarrow {{n_1}.} \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} \) \(= \dfrac{{\left| {{a_1}.{a_2} + {b_1}.{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\)
Hướng dẫn giải
Câu a:
Vectơ pháp tuyến \(\Delta_1\) là \(\overrightarrow {{n_1}} = (2;1)\)
Vectơ pháp tuyến \({\Delta _2}\) là \(\overrightarrow {{n_2}} = (5; - 2)\)
\(\eqalign{
& \cos ({\Delta _1},{\Delta _2}) = {{|\overrightarrow {{n_1}} .\overrightarrow {{n_2}} |} \over {|\overrightarrow {{n_1}} |.|\overrightarrow {{n_2}} |}} \cr&= {{|2.5 + 1.( - 2)|} \over {\sqrt {2^2+1^2} .\sqrt {5^2+(-2)^2} }}\cr& = {8 \over {\sqrt {145} }} \cr
& \Rightarrow ({\Delta _1},{\Delta _2}) \approx {48^0}21'59'' \cr} \)
Câu b:
\(y = -2x + 4 ⇔ 2x + y – 4 = 0\)
\(y = {1 \over 2}x + {3 \over 2} \Leftrightarrow x - 2y + 3 = 0\)
\({\Delta _1}\) có VTPT \(\overrightarrow {{n_1}} = \left( {2;1} \right)\)
\({\Delta _2}\) có VTPT \(\overrightarrow {{n_2}} = \left( {1;-2} \right)\)
\(\cos \left( {{\Delta _1},{\Delta _2}} \right) \) \(= \dfrac{{\left| {2.1 + 1.\left( { - 2} \right)} \right|}}{{\sqrt {{2^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} = 0\) \( \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = {90^0} \Rightarrow {\Delta _1} \bot {\Delta _2}\)
Cách khác:
- Hệ số góc của \(\Delta_1\) là \(k = -2\)
- Hệ số góc của \({\Delta _2}\) là \(k' = {1 \over 2}\)
Vì \(k.k' = 2.{1 \over 2} = - 1 \Rightarrow {\Delta _1} \bot {\Delta _2}\)
Hoặc
Vì \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 2.1 + 1.\left( { - 2} \right) = 0\) nên \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \)
Vậy \({\Delta _1} \bot {\Delta _2}\) hay góc giữa chúng bằng \(90^0\).
1.9. Giải bài 9 trang 93 SGK Hình học 10
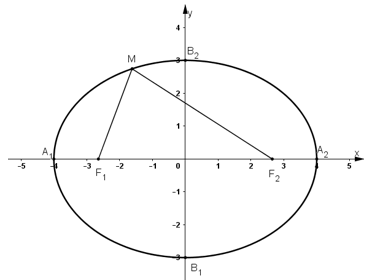
Cho elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) . Tìm tọa độ các đỉnh, các tiêu điểm và vẽ elip đó.
Phương pháp giải
Phương trình elip \((E) = {{{x^2}} \over {a^2}} + {{{y^2}} \over {b^2}} = 1\) có:
- Tọa độ các đỉnh: \(A_1(-a;0), A_2(a; 0), B_1(0; -b)\) và \(B_2(0; b)\)
- Các tiêu điểm: \(F_1(-c; 0)\) và \(F_2(c; 0)\) với \(c =\sqrt {a^2+b^2}\)
Hướng dẫn giải
Phương trình chính tắc của Elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) có dạng là:
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)
Ta có:
\(\eqalign{
& \left\{ \matrix{
{a^2} = 16 \hfill \cr
{b^2} = 9 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 4 \hfill \cr
b = 3 \hfill \cr} \right. \cr
& c = \sqrt {{a^2} - {b^2}} = \sqrt 7 \cr} \)
Tọa độ các đỉnh \(A_1(-4;0), A_2(4; 0), B_1(0; -3)\) và \(B_2(0; 3)\)
Tọa độ các tiêu điểm \(F_1(-\sqrt7; 0)\) và \(F_2(\sqrt7; 0)\)
1.10. Giải bài 10 trang 94 SGK Hình học 10
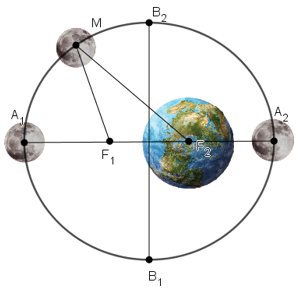
Ta biết rằng Mặt trăng chuyển động quanh Trái Đất theo một quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có chiều dài trục lớn và trục nhỏ lần lượt là \(769 266 km\) và \(768 106 km\). Tính khoảng cách ngắn nhất và khoảng cách dài nhất từ Trái Đất đến Mặt Trăng, biết rằng các khoảng cách đó đạt được khi Trái Đất và Mặt Trăng nằm trên trục lớn của Elip.
Phương pháp giải
- Khoảng cách ngắn nhất từ Mặt Trăng \(M\) đến Trái Đất \(F_2\) là \(F_2A_2\)
- Khoảng cách dài nhất từ Mặt Trăng \(M\) đến Trái Đất \(F_2\) là \(F_2A_1\)
Hướng dẫn giải
Ta thấy:
\(F_2A_2 = OA_2 – OF_2= a - c\)
\(F_2A_1 = OA_1 + OF_2= a + c\)
Ta biết:
\(2a = 769 266 ⇒ a = 384633\)
\(2b = 768 106 ⇒ b = 384 053\)
\(c^2= a^2– b^2\) \( ⇒ c ≈ 21115 (km)\)
Suy ra: \(F_2A_2 ≈ 384633-21115=363 518 (km)\), \(F_2A_1 ≈ 384633+21115=405 748 (km)\)
2. Câu hỏi trắc nghiệm
2.1. Giải bài 1 trang 94 SGK Hình học 10
Cho tam giác \(ABC\) có tọa độ các đỉnh \(A(1; 2), B(3; 1)\) và \(C(5; 4)\). Phương trình nào sau đây là phương trình đường cao của tam giác vẽ từ \(A\)?
A. \(2x + 3y – 8 = 0\)
B. \(3x – 2y – 5 = 0\)
C. \(5x – 6y + 7 = 0\)
D. \(3x – 2y + 5 = 0\)
Phương pháp giải
- Phương trình đường cao kẻ từ A của tam giác nhận vectơ BC làm VTPT.
- Viết phương trình đường thẳng đi qua điểm A biết VTPT.
Hướng dẫn giải
Đường cao kẻ từ A của tam giác ABC thì vuông góc với BC.
Phương trình đường cao kẻ từ A có VTPT: \(\overrightarrow {BC} = \left( {2;3} \right)\)
Phương trình đường cao đi qua điểm A(1;2) và có VTPT \(\overrightarrow {BC} = \left( {2;3} \right)\) là
\(\begin{array}{l}
2.\left( {x - 1} \right) + 3.\left( {y - 2} \right) = 0\\
\Leftrightarrow 2x + 3y - 8 = 0
\end{array}\)
Vậy A đúng.
2.2. Giải bài 2 trang 94 SGK Hình học 10
Cho tam giác \(ABC\) với \(A(-1; 1), B(4; 7)\) và \(C(3; -2)\). Phương trình tham số của trung tuyến CM là:
A. \(\left\{ \matrix{x = 3 + t \hfill \cr y = - 2 + 4t \hfill \cr} \right.\)
B. \(\left\{ \matrix{x = 3 + t \hfill \cr y = - 2 - 4t \hfill \cr} \right.\)
C. \(\left\{ \matrix{x = 3 - t \hfill \cr y = 4 + 2t \hfill \cr} \right.\)
D. \(\left\{ \matrix{x = 3 + 3t \hfill \cr y = - 2 + 4t \hfill \cr} \right.\)
Phương pháp giải
- Tìm tọa độ trung điểm M của AB
- Viết phưng trình đường thẳng đi qua hai điểm C và M đã biết toạn độ.
Hướng dẫn giải
Trung điểm \(M\) của \(AB\) có tọa độ: \(\left({3 \, \over 2}; \, 4\right)\)
\(\overrightarrow {CM} = \left( - {3 \over 2};6\right) = - {3 \over 2}(1;- 4)\)
Đường thẳng \(CM\) đi qua \(C\) và nhận vecto \(\overrightarrow a = (1; - 4)\) làm một vecto chỉ phương nên có phương trình tham số: \(\left\{ \matrix{x = 3 + t \hfill \cr y = - 2 - 4t \hfill \cr} \right.\)
Vậy chọn B.
2.3. Giải bài 3 trang 94 SGK Hình học 10
Cho phương trình tham số của đường thẳng \(d\): \(\left\{ \matrix{x = 5 + t \hfill \cr y = - 9 - 2t \hfill \cr} \right.\)
Trong các phương trình sau, phương trình nào là tổng quát của (d)?
A. \(2x + y – 1 = 0\)
B. \(2x + 3y + 1 = 0\)
C. \(x + 2y + 2 = 0\)
D. \(x + 2y – 2 = 0\)
Phương pháp giải
Thực hiện biến đổi tương đương khử mẫu để đưa phương trình tham số về phương trình tổng quát.
Hướng dẫn giải
Ta có phương trình tham số của đường thẳng:
\(\left\{ \matrix{
x = 5 + t \hfill \cr
y = - 9 - 2t \hfill \cr} \right. \Rightarrow \left\{ \matrix{
t = x - 5 \hfill \cr
y = - 9 - 2t \hfill \cr} \right.\)
Thay vào: \(y = -9 – 2( x – 5) ⇔ 2x + y – 1 = 0\)
Phương trình tổng quát: \(2x + y – 1 = 0\)
Chọn A.
2.4. Giải bài 4 trang 94 SGK Hình học 10
Đường thẳng đi qua điểm \(M(1; 0)\) và song song với đường thẳng \(d: 4x + 2y + 1 = 0\) có phương trình tổng quát là:
A. \(4x + 2y + 3 = 0\)
B. \(2x + y + 4 = 0\)
C. \(2x + y – 2 = 0\)
D. \(x – 2y + 3 = 0\)
Phương pháp giải
- Tìm VTPT của đường thẳng d.
- Viết PT đường thẳng đi qua 1 điểm và biết VTPT.
Hướng dẫn giải
\(d\) có VTPT \(\overrightarrow n = \left( {4;2} \right)\)
\(d'//d\) nên nhận \(\overrightarrow n = \left( {4;2} \right)\) làm VTPT.
Mà \(d'\) đi qua \(M (1; 0)\) nên:
\(4(x – 1) + 2 (y – 0) = 0 \) \(⇔ 2x + y – 2 = 0\)
Vậy chọn C.
2.5. Giải bài 5 trang 94 SGK Hình học 10
Đường thẳng đi qua điểm \(M(1; 0)\) và song song với đường thẳng \(d: 4x + 2y + 1 = 0\) có phương trình tổng quát là:
A. \(4x + 2y + 3 = 0\)
B. \(2x + y + 4 = 0\)
C. \(2x + y – 2 = 0\)
D. \(x – 2y + 3 = 0\)
Phương pháp giải
Tìm được VTPT của đường thẳng d cần viết.
Viết phương trình đường thẳng d đi qua 1 điểm và biết VTPT.
Hướng dẫn giải
\(d\) có VTPT \(\overrightarrow n = \left( {4;2} \right)\)
\(d'//d\) nên nhận \(\overrightarrow n = \left( {4;2} \right)\) làm VTPT.
Mà \(d'\) đi qua \(M (1; 0)\) nên:
\(4(x – 1) + 2 (y – 0) = 0 \) \(⇔ 2x + y – 2 = 0\)
Vậy chọn C.
2.6. Giải bài 6 trang 95 SGK Hình học 10
Bán kính của đường tròn tâm \(\displaystyle I(0; 2)\) và tiếp xúc với đường thẳng \(\displaystyle Δ: 3x – 4y – 23 = 0\) là:
A. \(\displaystyle 15\)
B. \(\displaystyle 5\)
C. \(\displaystyle {3 \over 5}\)
D. \(\displaystyle 3\)
Phương pháp giải
Bán kính của đường tròn tâm \(\displaystyle I(0; 2)\) và tiếp xúc với đường thẳng \(\displaystyle Δ: 3x – 4y – 23 = 0\) chính là khoảng cách tứ tâm đến đường thẳng Δ.
Hướng dẫn giải
Bán kính của đường tròn tâm \(\displaystyle I(0; 2)\) và tiếp xúc với đường thẳng \(\displaystyle Δ: 3x – 4y – 23 = 0\) là:
\(\displaystyle R = d(I,\, \, \Delta ) = {{|3.0 - 4.( - 2) - 23|} \over {\sqrt {9 + 16} }} \)
\( = \dfrac{{15}}{5} = 3\)
Vậy chọn D.
2.7. Giải bài 7 trang 95 SGK Hình học 10
Cho hai đường thẳng:
\(d_1: 2x + y + 4 – m = 0\)
\(d_2: (m + 3)x + y – 2m – 1 = 0\)
Đường thẳng \(d_1//d_2\) khi:
A. \(m = 1\) B. \(m = -1\)
C. \(m = 2\) D. \(m = 3\)
Phương pháp giải
Hai đường thẳng song song với nhau khi hệ số trước x và y bằng nhau và hệ số tự do khác nhau.
Hướng dẫn giải
Ta có:
\(d_1: 2x + y + 4 – m = 0\)
\(d_2: (m + 3)x + y – 2m – 1 = 0\)
Xét hệ phương trình:
\(\left\{ \matrix{
2x + y + 4 - m = 0 \hfill \cr
(m + 3)x + y - 2m - 1 = 0 \hfill \cr} \right.\)
Để \(d_1//d_2\) thì hệ phương trình trên vô nghiệm.
\(\begin{array}{l}
\Leftrightarrow \dfrac{{m + 3}}{2} = \dfrac{1}{1} \ne \dfrac{{ - 2m - 1}}{{4 - m}}\\
\Leftrightarrow \left\{ \begin{array}{l}
m + 3 = 2\\
- 2m - 1 \ne 4 - m
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
m = - 1\\
m \ne - 5
\end{array} \right. \Leftrightarrow m = - 1
\end{array}\)
Vậy chọn B.
2.8. Giải bài 8 trang 95 SGK Hình học 10
Cho \(d_1: x + 2y + 4 = 0\) và \(d_2: 2x – y + 6 = 0\). Số đo của góc giữa hai đường thẳng \(d_1\) và \(d_2\) là:
A. \(30^0\) B. \(60^0\)
C. \(45^0\) D. \(90^0\)
Phương pháp giải
Tìm VTPT của hai đường thẳng.
Tính góc giữa hai tiếp tuyến chính là góc giữa hai đoừng thẳng.
Hướng dẫn giải
Vecto pháp tuyến của \(d_1\) là \(\overrightarrow n = \left( {1;\;2} \right)\) và của \(d_2\) là: \( \overrightarrow u = \left( {2; - 1} \right).\)
Ta có: \(\overrightarrow n .\overrightarrow u = 1.2 + 2.( - 1) = 0 \Leftrightarrow \overrightarrow n \bot \overrightarrow u \)\( \Rightarrow ({d_1},{d_2}) = {90^0}\)
Vậy chọn D.
2.9. Giải bài 9 trang 95 SGK Hình học 10
Cho hai đường thẳng \(\Delta_1: x + y + 5 = 0\) và \(\Delta_2: y = -10.\) Góc giữa \(\Delta_1\) và \(\Delta_2\) là:
A. \(45^0\) B. \(30^0\)
C. \(88^057’52’’\) D. \(1^013’8’’\)
Phương pháp giải
Sử dụng công thức tính góc giữa hai đường thẳng
\(\cos \alpha = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} \) \(= \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\)
Hướng dẫn giải
Vecto pháp tuyến của \(\Delta_1\) là \(\overrightarrow {{n_1}} = (1;1)\) và của \(\Delta_2\) là \(\overrightarrow j = (0;1)\)
\(\cos ({\Delta _1},{\Delta _2}) \) \( = \dfrac{{\left| {1.0 + 1.1} \right|}}{{\sqrt {{1^2} + {1^2}} .\sqrt {{0^2} + {1^2}} }} = \dfrac{1}{{\sqrt 2 }}\)
\( \Rightarrow ({\Delta _1},{\Delta _2}) = {45^0}\)
Vậy chọn A.
2.10. Giải bài 10 trang 95 SGK Hình học 10
Khoảng cách từ điểm \(M(0; 3)\) đến đường thẳng \(Δ: x\cos α + y \sin α + 3(2 - \sin α) = 0\) là:
A. \(\sqrt6\) B. \(6\)
C. \(3\sin α\) D. \({3 \over {\sin \alpha + \cos \alpha }}\)
Phương pháp giải
Áp dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
Hướng dẫn giải
Khoảng cách từ điểm \(M(0; 3)\) đến đường thẳng \(Δ: x\cos α + y \sin α + 3(2 - \sin α) = 0\) là:
\(d(M,\Delta ) = {{|0.cos\alpha + 3.sin\alpha + 3(2 - \sin \alpha )|} \over {\sqrt {\sin {\alpha ^2} + \cos {\alpha ^2}} }} = 6\)
Vậy chọn B.
2.11. Giải bài 11 trang 95 SGK Hình học 10
Phương trình nào sau đây là phương trình đường tròn?
A. \(x^2+ 2y^2– 4x – 8y + 1 = 0\)
B. \(4x^2+ y^2– 10x – 6y -2 = 0\)
C. \(x^2+ y^2– 2x – 8y + 20 = 0\)
D. \(x^2+ y^2– 4x + 6y - 12 = 0\)
Phương pháp giải
Để phương trình có dạng : \(x^2+ y^2– 2ax – 2by + c = 0\) là phương trình của một đường tròn thì điều kiện : \( a^2+b^2-c > 0.\)
Hướng dẫn giải
Phương trình \(x^2+ y^2– 2x – 8y + 20 = 0\) không phải là phương trình của một đường tròn vì:
\( a^2+b^2-c = 1 + 16 – 20 = -3 < 0\)
Phương trình \(4x^2+ y^2– 10x – 6y -2 = 0\) và \(x^2+ 2y^2– 4x – 8y + 1 = 0\) không thuộc dạng :
\(x^2+ y^2– 2ax – 2by + c = 0\) nên không phải là phương trình của đường tròn.
Phương trình \(x^2+ y^2– 4x + 6y - 12 = 0\) là phương trình đường tròn \( a^2+b^2-c = 4 + 9 + 12 = 25 > 0\).
Vậy chọn D.
2.12. Giải bài 12 trang 95 SGK Hình học 10
Cho đường tròn (C): \(x^2+ y^2+ 2x + 4y – 20 = 0\)
Tìm mệnh đề sai trong các mệnh đề sau:
A. (C) có tâm \(I(1; 2)\)
B. (C) có bán kính \(R = 5\)
C. (C) đi qua điểm \(M(2; 2)\)
D. (C) không đi qua \(A(1; 1)\)
Phương pháp giải
Viết phương trình đường tròn về dạng : \((x-a)^2+(y-b)^2=R^2\).
Xác định tâm và bán kính của đường tròn rồi đối chiếu để kết luận đáp án sai.
Hướng dẫn giải
Ta có đường tròn \((C) )\): \(x^2+ y^2+ 2x + 4y – 20 = 0\)
\(a=-1,b=-2,c=-20\) \(R = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2} + 20} = 5\)
Đường tròn có tâm \(I(-1; -2)\) và bán kính \(R = 5\) nên A sai, B đúng.
- Thay \(M(2; 2)\) vào phương trình ta có: \({2^2} + {2^2} + 2.2 + 4.2 - 20 = 0\) nên \(M ∈ (C)\) nên C đúng.
- Thay \(A(1; 1)\) vào phương trình , ta có: \({1^2} + {1^2} + 2.1 + 4.1 - 20 = - 12 \ne 0\) nên \(A ∉ (C)\) nên D đúng.
Vậy chọn A.
2.13. Giải bài 13 trang 95 SGK Hình học 10
Phương trình tiếp tuyến tại điểm \(M(3; 4)\) với đường tròn \((C): x^2+y^2– 2x – 4y – 3 = 0.\)
A.\( x + y – 7 = 0\)
B.\( x + y + 7 = 0\)
C.\( x – y – 7 = 0\)
D. \(x + y – 3 = 0\)
Phương pháp giải
Đưa phương trinhd đường tròn về dạng tổng quát để xác định tâm và bán kính chủa đường tròn.
Phương trình tiếp tuyến đi qua điểm M có VTPT chính là vectơ OM với O là tâm của đường tròn.
Hướng dẫn giải
Đường tròn \((C): x^2+y^2– 2x – 4y – 3 = 0\) có \(a=1,b=2,c=-3\) nên có tâm \(I(1;2)\) và bán kính \(R = \sqrt {{1^2} + {2^2} + 3} = \sqrt 8 \).
\(\overrightarrow {IM} = \left( {2;2} \right)\)
Gọi d là phương trình tiếp tuyến tại M với (C)
⇒ IM ⊥ d
⇒ d đi qua M(3;4) và nhận \(\overrightarrow {IM} = (2,2)\) làm vecto pháp tuyến.
\(⇒d:2(x – 3) + 2(y – 4) = 0 \) \(⇔ x + y – 7 = 0\)
Vậy chọn A.
2.14. Giải bài 14 trang 96 SGK Hình học 10
Cho đường tròn (C) : \(x^2+ y^2– 4x – 2y = 0\) và đường thẳng \(Δ: x + 2y + 1 = 0\)
Trong các mệnh đề sau, tìm mệnh đề đúng:
A. \(Δ\) đi qua tâm \((C)\)
B. \(Δ\) cắt \((C)\) tại hai điểm
C. \(Δ\) tiếp xúc \((C)\)
D. \(Δ\) không có điểm chung với \((C)\)
Phương pháp giải
Tính khoảng cách d từ tâm O của đường tròn đến đường thẳng Δ rồi so sánh với bán kính của đường tròn.
- d>R thì \(Δ\) không có điểm chung với \((C)\)
- d=R thì \(Δ\) tiếp xúc \((C)\).
- d
Hướng dẫn giải
Đường tròn \((C):x^2+ y^2– 4x – 2y = 0 \)\(\Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 5\) có tâm \(I(2; 1)\) và bán kính \(R = \sqrt5.\)
Khoảng cách từ tâm \(I\) đến đường thẳng \(Δ: x + 2y + 1 = 0\) là:
\(d\left( {I,\;\Delta } \right) = \frac{{\left| {2 + 2 + 1} \right|}}{{\sqrt 5 }} = \sqrt 5 =R.\)
Do đó \(Δ\) tiếp xúc với \((C).\)
Vậy C đúng.
2.15. Giải bài 15 trang 96 SGK Hình học 10
Đường tròn \(\displaystyle (C): x^2+ y^2– x + y – 1 = 0\) có tâm \(\displaystyle I\) và bán kính \(\displaystyle R\) là:
A. \(\displaystyle I(-1; \, 1); R = 1\)
B. \(\displaystyle I({1 \over 2}; - {1 \over 2});R = {{\sqrt 6 } \over 2}\)
C. \(\displaystyle I( - {1 \over 2};{1 \over 2});R = {{\sqrt 6 } \over 2}\)
D. \(\displaystyle I(1; -1); R = \sqrt6\)
Phương pháp giải
Viết phương trình đường tròn về dạng tổng quát ròi suy ra tâm và bán kính.
Hướng dẫn giải
\((C): x^2+ y^2– x + y – 1 = 0\) có \(a = \dfrac{1}{2},b = - \dfrac{1}{2},c = - 1\)
nên (C) có tâm \(I\left( {\dfrac{1}{2}; - \dfrac{1}{2}} \right)\) bán kính \(R = \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( { - \dfrac{1}{2}} \right)}^2} + 1} = \dfrac{{\sqrt 6 }}{2}\)
Vậy chọn B.
2.16. Giải bài 16 trang 96 SGK Hình học 10
Với giá trị nào của m thì phương trình sau đây là phương trình của đường tròn: \(x^2+ y^2– 2(m+2)x + 4my + 19m – 6 \)\(= 0\)
A. \(1 < m < 2\)
B. \(-2 ≤ m ≤ 1\)
C. \(m < 1\) hoặc \(m > 2\)
D. \(m < -2\) hoặc \(m > 1\)
Phương pháp giải
Đưa phương trình đương tròn về dạng tổng quát,
Tìm điều kiện của m để \(R^2\) tương ứng lớn hơn 0.
Hướng dẫn giải
Ta có: \(a = m + 2 ; b = -2m ; c = 19m – 6\)
Phương trình đã cho là đường tròn
\(\begin{array}{l}
\Leftrightarrow {a^2} + {b^2} - c > 0\\
\Leftrightarrow {\left( {m + 2} \right)^2} + {\left( { - 2m} \right)^2} - \left( {19m - 6} \right) > 0\\
\Leftrightarrow {m^2} + 4m + 4 + 4{m^2} - 19m + 6 > 0\\
\Leftrightarrow 5{m^2} - 15m + 10 > 0\\
\Leftrightarrow \left[ \begin{array}{l}
m < 1\\
m > 2
\end{array} \right.
\end{array}\)
Vậy chọn C.
2.17. Giải bài 17 trang 96 SGK Hình học 10
Đường thẳng \(Δ: 4x + 3y + m = 0\) tiếp xúc với đường tròn \((C): x^2+ y^2=1\) khi:
A. \(m = 3\) B. \(m = 5\)
C. \(m = 1\) D. \(m = 0\)
Phương pháp giải
Đường thẳng \(Δ\) tiếp xúc với đường tròn \((C)\) khi khoảng cách từ tâm của đường tròn đến dường thẳng \(Δ\) bằng R.
Hướng dẫn giải
\((C)\) là đường tròn tâm \(O (0; \, 0)\) bán kính \(R=1.\)
Để đường thẳng \(Δ: 4x + 3y + m = 0\) tiếp xúc với đường tròn \((C): x^2+ y^2=1\) thì:
\(\eqalign{
& d(O,\Delta ) = R \Leftrightarrow {{|4.0 + 3.0 + m|} \over {\sqrt {{4^2} + {3^2}} }} = 1 \cr & \Leftrightarrow \frac{{\left| m \right|}}{5} = 1 \Leftrightarrow \left| m \right| = 5\cr
& \Leftrightarrow m = \pm 5 \Rightarrow m = 5 \cr} \)
Vậy chọn B.
2.18. Giải bài 18 trang 96 SGK Hình học 10
Cho hai điểm \(A(1; 1)\) và \(B(7; 5)\). Phương trình đường tròn đường kính \(AB\) là:
A. \(x^2+ y^2 + 8x + 6y + 12 = 0\)
B. \(x^2+ y^2- 8x - 6y + 12 = 0\)
C. \(x^2+ y^2- 8x - 6y - 12 = 0\)
D. \(x^2+ y^2+ 8x + 6y - 12 = 0\)
Phương pháp giải
Lập phương trình đường tròn có:
Tâm I là trung điểm của đoạn thẳng AB.
Bán kính R bằng một nửa đường kính AB.
Hướng dẫn giải
Tâm đường tròn là trung điểm I của đoạn thẳng AB
A(1 ; 1) ; B(7 ; 5) ⇒ I(4; 3)
Bán kính đường tròn
\(R = \dfrac{{AB}}{2} = \dfrac{{\sqrt {{{\left( {7 - 1} \right)}^2} + {{\left( {5 - 1} \right)}^2}} }}{2} = \sqrt {13} \)
⇒ đường tròn đường kính AB là:
\(\begin{array}{l}
{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = {\left( {\sqrt {13} } \right)^2}\\
\Leftrightarrow {\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 13\\
\Leftrightarrow {x^2} - 8x + 16 + {y^2} - 6y + 9 - 13 = 0\\
\Leftrightarrow {x^2} + {y^2} - 8x - 6y + 12 = 0
\end{array}\)
Chọn C.
2.19. Giải bài 19 trang 96 SGK Hình học 10
Đường tròn đi qua ba điểm \(A(0; 2); B(-2; 0)\) và \(C(2; 0)\) có phương trình là:
A. \(x^2+ y^2 =8\)
B. \(x^2+ y^2+ 2x + 4 = 0\)
C. \(x^2+ y^2- 2x - 8 = 0\)
D. \(x^2+ y^2- 4 = 0\)
Phương pháp giải
Gọi phương trình đường tròn rồi lập hệ phương trình ba ẩn để giải.
Hướng dẫn giải
Gọi phương trình đường tròn cần tìm \((C) : x^2+ y^2– 2ax – 2by + c = 0\) với \(a^2+b^2-c> 0\).
\(A\left( {0;2} \right) \in \left( C \right) \) \(\Leftrightarrow {0^2} + {2^2} - 2a.0 - 2b.2 + c = 0 \) \(\Leftrightarrow 4 - 4b + c = 0\)
\(B\left( {-1;0} \right) \in \left( C \right) \) \(\Leftrightarrow {(-2)^2} + {0^2} - 2a.(-2) - 2b.0 + c = 0 \) \(\Leftrightarrow 4 + 4a + c = 0\)
\(C\left( {2;0} \right) \in \left( C \right) \) \(\Leftrightarrow {2^2} + {0^2} - 2a.2 - 2b.0 + c = 0 \) \(\Leftrightarrow 4 - 4a + c = 0\)
Ta có hệ:
\(\left\{ \matrix{
4 - 4b + c = 0 \hfill \cr
4 + 4a + c = 0 \hfill \cr
4 - 4a + c = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 0 \hfill \cr
b = 0 \hfill \cr
c = - 4 \hfill \cr} \right.\)
Vậy phương trình đường tròn \((C)\) là: \(x^2+ y^2- 4 = 0\)
Do đó chọn D.
2.20. Giải bài 20 trang 96 SGK Hình học 10
Cho điểm \(M(0; 4)\) và đường tròn \((C)\) có phương trình: \(x^2+ y^2- 8x – 6y + 21 = 0\)
Trong các phát biểu sau, tìm phát biểu đúng:
A. \(M\) nằm ngoài \((C)\)
B. \(M\) nằm trên \((C)\)
C. \(M\) nằm trong \((C)\)
D. \(M\) trùng với tâm của \((C)\)
Phương pháp giải
Tính khoảng cách từ điểm M đến tâm của đường tròn C rồi so sánh với bán kính R của đường tròn C để rút ra kết luận.
Hướng dẫn giải
Đường tròn: \(x^2+ y^2- 8x – 6y + 21 = 0\) có \(a=4;b=3;c=21\) nên có tâm \(I (4; 3)\) và bán kính \(R = \sqrt {{4^2} + {3^2} - 21} = 2\)
Ta có: \(MI = \sqrt {{{\left( {4 - 0} \right)}^2} + {{\left( {4 - 3} \right)}^2}} = \sqrt {17} \)\( \approx 4,12 > R\) nên \(M\) nằm ngoài \((C).\)
Vậy chọn A.
2.21. Giải bài 21 trang 96 SGK Hình học 10
Cho elip \((E)\): \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\) và cho các mệnh đề:
(I) \((E)\) có tiêu điểm \(F_1( -4; 0)\) và \(F_2( 4; 0)\)
(II) \((E)\) có tỉ số \({c \over a} = {4 \over 5}\)
(III) \((E)\) có đỉnh \(A_1(-5; 0)\)
(IV) \((E)\) có độ dài trục nhỏ bằng \(3\).
Trong các mệnh đề sau, tìm mệnh đề sai:
A. (I)
B. (II)
C. (I)
D. (IV)
Phương pháp giải
Phương trình elip \((E) = {{{x^2}} \over {a^2}} + {{{y^2}} \over {b^2}} = 1\) có:
- Tọa độ các đỉnh: \(A_1(-a;0), A_2(a; 0), B_1(0; -b)\) và \(B_2(0; b)\)
- Các tiêu điểm: \(F_1(-c; 0)\) và \(F_2(c; 0)\) với \(c =\sqrt {a^2+b^2}\)
Hướng dẫn giải
\((E)\): \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\) có \(a^2= 25, b^2= 9, c^2= a^2– b^2= 16\)
\(⇒ a = 5; b = 3\) và \(c = 4\)
Tiêu điểm \(F_1( -4; 0)\) và \(F_2( 4; 0)\) nên (I) đúng.
Đỉnh \(A_1(-5; 0), A_2(5; 0),\) \( B_1(0; -3), B_2(0; 3)\) nên (III) đúng
Độ dài trục nhỏ \(2b = 6\) nên (IV) sai
\((E)\) có tỉ số \({c \over a} = {4 \over 5}\) nên (II) đúng
Từ đó suy ra, mệnh đề sai là (IV).
Chọn D.
2.22. Giải bài 22 trang 97 SGK Hình học 10
Phương trình chính tắc của elip có hai đỉnh là \(\displaystyle (-3; 0), (3; 0)\) và hai tiêu điểm là \(\displaystyle (-1; 0), (1; 0)\) là:
A. \(\displaystyle {{{x^2}} \over 9} + {{{y^2}} \over 1} = 1\)
B. \(\displaystyle {{{x^2}} \over 8} + {{{y^2}} \over 9} = 1\)
C. \(\displaystyle {{{x^2}} \over 9} + {{{y^2}} \over 8} = 1\)
D. \(\displaystyle {{{x^2}} \over 1} + {{{y^2}} \over 9} = 1\)
Phương pháp giải
Phương trình chính tắc của (E): \(\displaystyle {{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\) với \(\displaystyle a^2=b^2+c^2.\)
Hướng dẫn giải
(E) có hai đỉnh \(\displaystyle A_1(-3; 0) \) và \(\displaystyle A_2(3; 0)\) nên a = 3
(E) có hai tiêu điểm \(\displaystyle F_1(-1; 0) \) và \(\displaystyle F_2(1; 0)\) nên c = 1
\(\displaystyle a = 3\) và \(\displaystyle c = 1\), suy ra: \(\displaystyle b^2= a^2– c^2= 8\)
Phương trình chính tắc của \(\displaystyle (E)\): \(\displaystyle {{{x^2}} \over 9} + {{{y^2}} \over 8} = 1\)
Vậy chọn C.
2.23. Giải bài 23 trang 97 SGK Hình học 10
Cho elip \(\displaystyle (E): x^2+ 4y^2= 1\) và cho các mệnh đề:
(I): \(\displaystyle (E)\) có trục lớn bằng \(\displaystyle 1\)
(II) \(\displaystyle (E)\) có trục nhỏ bằng \(\displaystyle 4\)
(III) \(\displaystyle (E)\) có tiêu điểm \(\displaystyle {F_1}(0; \, {{\sqrt 3 } \over 2})\)
(IV) \(\displaystyle (E)\) có tiêu cự bằng \(\displaystyle \sqrt3\).
Trong các mệnh đề sau, tìm mệnh đề đúng:
A. (I) B. (II) và (IV)
C. (I) và (III) D. (IV)
Phương pháp giải
- Độ dài trục lớn \(2a = 2\) nên (I) sai
- Độ dài trục nhỏ \(2b = 1\) nên (II) sai
- Tiêu cự \(2c = \sqrt3\) nên (IV) đúng
Hướng dẫn giải
Elip:
\(\eqalign{
& {x^2} + 4{y^2} = 1 \Leftrightarrow {{{x^2}} \over 1} + {{{y^2}} \over {{1 \over 4}}} = 1 \cr
& {a^2} = 1;{b^2} = {1 \over 4},{c^2} = {a^2} - {b^2} = {3 \over 4}\cr& \Rightarrow \left\{ \matrix{
a = 1 \hfill \cr
b = {1 \over 2} \hfill \cr
c = {{\sqrt 3 } \over 2} \hfill \cr} \right. \cr} \)
Độ dài trục lớn \(2a = 2\) nên (I) sai
Độ dài trục nhỏ \(2b = 1\) nên (II) sai
Tiêu cự \(2c = \sqrt3\) nên (IV) đúng
Tiêu điểm \({F_1}( - {{\sqrt 3 } \over 2};0)\) \({F_2}({{\sqrt 3 } \over 2}; \, 0)\) nên (III) sai.
Vậy chỉ có mệnh đề (IV) đúng.
Vậy chọn D.
2.24. Giải bài 24 trang 97 SGK Hình học 10
Dây cung của elip (E): \(\displaystyle {{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1 (0 < b < a)\) vuông góc với trục lớn tại tiêu điểm có độ dài là:
A. \(\displaystyle {{2{c^2}} \over a}\) B. \(\displaystyle {{2{b^2}} \over a}\)
C. \(\displaystyle {{2{a^2}} \over c}\) D. \(\displaystyle {{{a^2}} \over c}\)
Phương pháp giải
- Viết phương trình đường thẳng \(Δ\) đi qua tiêu điểm và vuông góc với trục lớn.
- Tìm tọa độ giao điểm của \(Δ\) và elip
- Tính độ dài đoạn thẳng nối 2 giao điểm vừa tìm được chính là độ dài cần tìm.
Hướng dẫn giải
Gọi đường thẳng \(Δ\) đi qua tiêu điểm \(F_2(c; 0)\) của elip (E) và vuông góc với trục lớn.
Khi đó \(\Delta //Oy\) và \({F_2}\left( {c;0} \right) \in \Delta \) nên \(\Delta :x - c = 0\)
\(Δ\) cắt \((E)\) tại hai điểm \(M\) và \(N\) có tọa độ là nghiệm của hệ phương trình:
\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
x = c\\
\dfrac{{{c^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = c\\
\dfrac{{{a^2} - {b^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = c\\
1 - \dfrac{{{b^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} - 1 = 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = c\\
\dfrac{{{y^2}}}{{{b^2}}} = \dfrac{{{b^2}}}{{{a^2}}}
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = c\\
{y^2} = \dfrac{{{b^4}}}{{{a^2}}}
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = c\\
y = \pm \dfrac{{{b^2}}}{a}
\end{array} \right.\\
\Rightarrow M\left( {c;\dfrac{{{b^2}}}{a}} \right),N\left( {c; - \dfrac{{{b^2}}}{a}} \right)
\end{array}\)
\( \Rightarrow MN = \sqrt {{{\left( {c - c} \right)}^2} + {{\left( { - \dfrac{{{b^2}}}{a} - \dfrac{{{b^2}}}{a}} \right)}^2}} \) \(= \sqrt {0 + \dfrac{{4{b^4}}}{{{a^2}}}} = \dfrac{{2{b^2}}}{a}\)
Vậy độ dài dây cung của \((E)\) là độ dài đoạn thẳng \(MN = {{2{b^2}} \over a}\).
Chọn B.
2.25. Giải bài 25 trang 97 SGK Hình học 10
Một elip có trục lớn là \(\displaystyle 26\), tỉ số \(\displaystyle {c \over a} = {{12} \over {13}}\) . Trục nhỏ của elip bằng bao nhiêu?
A. \(\displaystyle 5\) B. \(\displaystyle 10\)
C. \(\displaystyle 12\) D. \(\displaystyle 14\)
Phương pháp giải
- Độ dài trục lớn bằng 2a nên tìm được a
- Từ tỉ số tìm được c.
- Áp dụng công thức \({b^2} = {a^2} - {c^2}\) tìm được b. Từ đó tìm được độ dài trục nhỏ bằng 2b.
Hướng dẫn giải
Elip có trục lớn bằng \(26\) nên \(2a = 26 \Leftrightarrow a = 13\)
Ta có: \(\dfrac{c}{a} = \dfrac{{12}}{{13}} \)\( \Rightarrow \dfrac{c}{{13}} = \dfrac{{12}}{{13}} \Leftrightarrow c = 12\)
Lại có: \({b^2} = {a^2} - {c^2} = {13^2} - {12^2} = 25\)\( \Rightarrow b = 5.\)
Trục nhỏ bằng: \(2b=10.\)
Vậy chọn B.
2.26. Giải bài 26 trang 97 SGK Hình học 10
Cho elip \(\displaystyle (E): 4x^2+ 9y^2= 36\). Trong các mệnh đề sau, tìm mệnh đề sai:
A. \(\displaystyle (E)\) có trục lớn bằng \(\displaystyle 6\)
B. \(\displaystyle (E)\) có trục nhỏ bằng \(\displaystyle 4\)
C. \(\displaystyle (E)\) có tiêu cự bằng \(\displaystyle \sqrt5\)
D. \(\displaystyle (E)\) có tỉ số \(\displaystyle {c \over a} = {{\sqrt 5 } \over 3}\)
Phương pháp giải
Độ dài trục nhỏ \(2b \)
Độ dài trục lớn \(2a \)
Tiêu cự \(2c\)
Hướng dẫn giải
\(\eqalign{& 4{x^2} + {\rm{ }}9{y^2} = {\rm{ }}36 \Leftrightarrow {{{x^2}} \over 9} + {{{y^2}} \over 4} = 1 \cr & \left\{ \matrix{{a^2} = 9 \hfill \cr {b^2} = 4 \hfill \cr {c^2} = {a^2} - {b^2} = 5 \hfill \cr} \right. \Rightarrow \left\{ \matrix{a = 3 \hfill \cr b = 2 \hfill \cr c = \sqrt 5 \hfill \cr} \right. \cr} \)
Độ dài trục lớn \(2a = 6\), độ dài trục nhỏ \(2b = 4\) nên A, B đúng.
Tiêu cự \(2c = 2\sqrt5\) nên C sai.
Tỉ số \(\displaystyle {c \over a} = {{\sqrt 5 } \over 3}\) nên D đúng.
Vậy chọn C.
2.27. Giải bài 27 trang 98 SGK Hình học 10
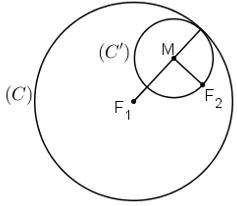
Cho đường tròn \((C)\) tâm \(F_1\) bán kính \(2a\) và một điểm \(F_2\) ở bên trong của \((C)\). Tập hợp tâm \(M\) của các đường tròn \((C’)\) thay đổi nhưng luôn đi qua \(F_2\) và tiếp xúc với \((C)\) (xem hình) là đường nào sau đây?
A. Đường thẳng
B. Đường tròn
C. Elip
D. Parabol
Phương pháp giải
\((C’)\) tiếp xúc trong với đường tròn \((C)\) nên \(F_1M = 2a – r\)
Hướng dẫn giải
Gọi bán kính của đường tròn \((C’)\) là \(r\)
Ta có: \((C’)\) tiếp xúc trong với đường tròn \((C)\) nên \(F_1M = 2a – r\)
\(F_2 ∈ (C’)\) nên \(F_2M = r\)
Ta có: \(F_1M + F_2M = 2a – r + r = 2a\)
Suy ra: Tập hợp tâm \(M\) của đường tròn \((C’)\) là một elip có hai tiêu điểm \(F_1,F_2\) cố định và độ dài trục lớn bằng \(2a\).
Vậy chọn C.
2.28. Giải bài 28 trang 98 SGK Hình học 10
Khi \(t\) thay đổi, điểm \(M(5\cos t; 4\sin t)\) di động trên đường nào sau đây:
A. Elip B. Đường thẳng
C. Parabol D. Đường tròn
Phương pháp giải
Biến đổi phương trình để được đường tròn.
Hướng dẫn giải
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
x_M = 5\cos t\\
y_M = 4\sin t
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
\dfrac{x_M}{5} = \cos t\\
\dfrac{y_M}{4} = \sin t
\end{array} \right.\\
\Rightarrow {\left( {\dfrac{x_M}{5}} \right)^2} + {\left( {\dfrac{y_M}{4}} \right)^2} = {\cos ^2}t + {\sin ^2}t\\
\Leftrightarrow \dfrac{{{x_M^2}}}{{25}} + \dfrac{{{y_M^2}}}{{16}} = 1
\end{array}\)
Vậy điểm \(M\) di động trên Elip \(\displaystyle {{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1\)
Vậy chọn A.
2.29. Giải bài 29 trang 98 SGK Hình học 10
Cho elip \((E)\): \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1(0 < b < a)\). Gọi \(F_1,F_2\) là hai tiêu điểm và cho điểm \(M(0; -b)\). Giá trị nào sau đây bằng giá trị của biểu thức : \(MF_1. MF_2– OM^2\)
A. \(c^2\) B. \(2a^2\)
C. \(2b^2\) D. \(a^2– b^2\)
Phương pháp giải
- Tọa độ tiêu điểm \(F_1=(-a,0); F_2= (a;0)\)
- Tính \(MF_1; MF_2;OM\)
Hướng dẫn giải
Ta có: \(M\left( {0; - b} \right),{F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\)
\(M{F_1} = \sqrt {{{\left( { - c} \right)}^2} + {b^2}} = \sqrt {{b^2} + {c^2}} = a\)
\(M{F_2} = \sqrt {{{c}^2} + {b^2}} = a\)
\(O{M^2} = {0^2} + {\left( { - b} \right)^2} = {b^2}\)
\(MF_1MF_2 – OM^2= a^2– b^2= c^2\).
Vậy chọn A và D đều đúng.
2.30. Giải bài 30 trang 98 SGK Hình học 10
Cho elip \(\displaystyle (E) {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) và đường thẳng \(\displaystyle Δ: y + 3 = 0\). Tích các khoảng cách từ hai tiêu điểm của \(\displaystyle (E)\) đến đường thẳng \(\displaystyle Δ\) bằng các giá trị nào sau đây:
A. \(\displaystyle 16\) B. \(\displaystyle 9\)
C. \(\displaystyle 81\) D. \(\displaystyle 7\)
Phương pháp giải
- Tìm tọa độ hai tiêu điểm.
- Tính khoảng cách từ các tiêu điểm đến đường thẳng suy ra đáp số.
Hướng dẫn giải
Elip \(\displaystyle (E) :{{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\)
Ta có:
\(\left\{ \begin{array}{l}
{a^2} = 16\\
{b^2} = 9\\
{c^2} = {a^2} - {b^2}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
a = 4\\
b = 3\\
c = \sqrt 7
\end{array} \right.\)
Hai tiêu điểm \(F_1(-\sqrt7; 0)\) và \(F_2(\sqrt7; 0)\)
\(\begin{array}{l}
d\left( {{F_1},\Delta } \right) = \dfrac{{\left| {0 + 3} \right|}}{{\sqrt {{0^2} + {1^2}} }} = 3\\
d\left( {{F_2},\Delta } \right) = \dfrac{{\left| {0 + 3} \right|}}{{\sqrt {{0^2} + {1^2}} }} = 3
\end{array}\)
\( \Rightarrow \) \(d(F_1, Δ).d(F_2, Δ)=3.3\) \(= 9\)
Vậy chọn B.
Tham khảo thêm
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 1: Phương trình đường thẳng
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 2: Phương trình đường tròn
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 3: Phương trình đường Elip