Giải bài tập SGK Toán 11 Bài 1: Vectơ trong không gian

Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Mặt phẳng (P) cắt các cạnh bên AA', BB', CC', DD' lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ:

a) Cùng phương với \(\overrightarrow {IA} \);

b) Cùng hướng với ​\(\overrightarrow {IA} \);

c) Ngược hướng với ​\(\overrightarrow {IA} \).

Phương pháp giải:

- Các vectơ được gọi là cùng phương khi và chỉ khi giá của các vectơ đó song song hoặc trùng nhau.

- Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.

Hướng dẫn giải:

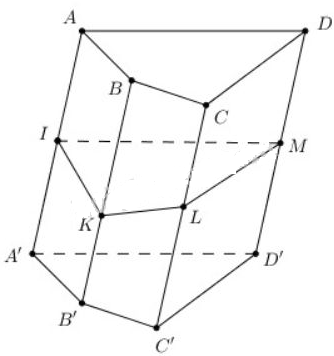
a) Các véctơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ mà cùng phương với \(\overrightarrow {IA} \) là: \(\overrightarrow {IA'} , \ \overrightarrow {KB} ,\ \overrightarrow {KB'} , \ \overrightarrow {LC} , \ \overrightarrow {LC'} ,\ \overrightarrow {MD} ,\ \overrightarrow {MD'} \).

b) Các véctơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ mà cùng hướng với \(\overrightarrow {IA} \) là: \(\ \overrightarrow {KB} , \ \overrightarrow {LC} ,\ \overrightarrow {MD} \).

c) Các véctơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ mà ngược hướng với \(\overrightarrow {IA} \) là: \(\overrightarrow {IA'} ,\ \overrightarrow {KB'} , \ \overrightarrow {LC'} ,\ \overrightarrow {MD'} \).

Cho hình hộp ABCD. A'B'C'D'. Chứng minh rằng:

a) \(\overrightarrow{AB}+\overrightarrow{B'C'}+\overrightarrow{DD'}=\overrightarrow{AC'}\);

b) \(\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{BB'}\);

c) \(\overrightarrow{AC}+\overrightarrow{BA'}+\overrightarrow{DB}+\overrightarrow{C'D}=\overrightarrow{0}\).

Phương pháp giải:

Biến đổi VT = VP bằng cách sử dụng các vectơ bằng nhau và quy tắc ba điểm.

Hướng dẫn giải:

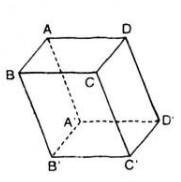
a) Ta có: \(\overrightarrow{B'C'}\ =\overrightarrow{BC}\), \(\overrightarrow{DD'}\ =\overrightarrow{CC'}\).

Suy ra \(\overrightarrow{AB}+\overrightarrow{B'C'}+\overrightarrow{DD'}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC'}=\overrightarrow{AC'}\).

b) Ta có: \(\overrightarrow{DD'}\ =-\overrightarrow{D'D}\), \(\overrightarrow{B'D'}\ =-\overrightarrow{D'B'}\).

Suy ra \(\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{BD}+\overrightarrow{DD'}+\overrightarrow{D'B'}=\overrightarrow{BB'}\).

c) Ta có: \(\overrightarrow{BA'}\ =\overrightarrow{CD'}\), \(\overrightarrow{DB}\ =\overrightarrow{D'B'}\), \(\overrightarrow{C'D}\ =\overrightarrow{B'A}\).

Suy ra

\(\begin{array}{l} \overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} \\ = \overrightarrow {AC} + \overrightarrow {CD'} + \overrightarrow {D'B'} + \overrightarrow {B'A} \\ = \overrightarrow {AD'} + \overrightarrow {D'B'} + \overrightarrow {B'A} \\ = \overrightarrow {AB'} + \overrightarrow {B'A} \\ = \overrightarrow 0 . \end{array}\)

Cho hình bình hành ABCD. Gọi S là một điểm nằm ngoài mặt phẳng chứa hình bình hành. Chứng minh rằng: \(\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}\).

Phương pháp giải:

Chứng minh VT và VP cùng bằng đại lượng trung gian bằng cách áp dụng quy tắc trung điểm.

Hướng dẫn giải:

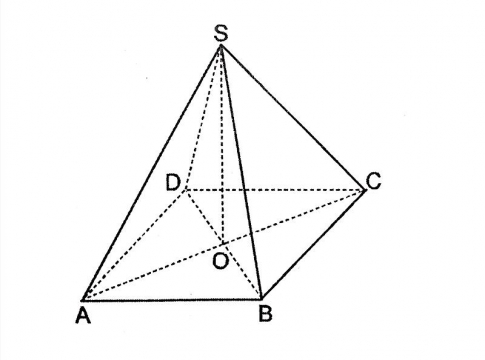
Gọi O là tâm của hình bình hành ABCD. Khi đó: O là trung điểm của AC, BD.

O là trung điểm của AC => \(\overrightarrow{SA} +\overrightarrow{SC}= 2\overrightarrow{SO}\) (quy tắc trung điểm).

O là trung điểm của tam giác BD => \(\overrightarrow{SB} +\overrightarrow{SD}= 2\overrightarrow{SO}\) (quy tắc trung điểm).

Suy ra: \(\overrightarrow{SA} +\overrightarrow{SC}=\overrightarrow{SB} +\overrightarrow{SD}\) (đpcm).

Cho hình tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng:

a) \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AD}+\overrightarrow{BC} \right )\);

b) \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AC}+\overrightarrow{BD} \right )\).

Phương pháp giải:

Chứng minh VT = VP bằng cách áp dụng quy tắc ba điểm và quy tắc trung điểm.

Hướng dẫn giải:

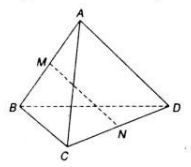
a) Ta có: 

\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}.\)

\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}.\)

Cộng từng vế ta được: 

\(2.\overrightarrow{MN} =(\overrightarrow{MA}+\overrightarrow{MB})+\overrightarrow{AD}+\overrightarrow{BC}+(\overrightarrow{DN}+\overrightarrow{CN})\).

Lại có:

M là trung điểm AB nên: \(\overrightarrow{MA}+\overrightarrow{MB} =0\).

N là trung điểm CD nên: \(\overrightarrow{DN}+\overrightarrow{CN} =0\).

Suy ra \(2.\overrightarrow{MN} = \overrightarrow{AD}+\overrightarrow{BC}\).

Vậy \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AD}+\overrightarrow{BC} \right )\).

b) Ta có:

\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN}\).

\(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BD} + \overrightarrow {DN}\).

Cộng từng vế ta được:

\(2.\overrightarrow{MN} =(\overrightarrow{MA}+\overrightarrow{MB})+\overrightarrow{AC}+\overrightarrow{BD}+(\overrightarrow{DN}+\overrightarrow{CN})\)

Suy ra \(2.\overrightarrow{MN} = \overrightarrow{AC}+\overrightarrow{BD}\).

Vậy \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AC}+\overrightarrow{BD} \right )\).

Cho hình tứ diện ABCD. Hãy xác định hai điểm E, F sao cho:

a) \(\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD};\)

b) \(\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AD}.\)

Phương pháp giải:

Áp dụng quy tắc hình bình hành: \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) với ABCD là hình bình hành để xác định điểm E và F.

Hướng dẫn giải:

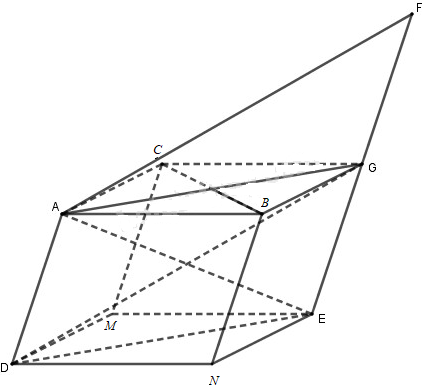
a) Gọi G là đỉnh thứ tư của hình bình hành ABGC, ta có: 

\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AG}\) (quy tắc hình bình hành).

Lại có: \(\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\) (giả thiết).

\(\Rightarrow \overrightarrow{AE}=\overrightarrow{AG}+\overrightarrow{AD}\).

Vậy E là đỉnh của hình bình hành ADEG.

b) Ta có:

\(\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AD}\) (giả thiết).

\(\Rightarrow \overrightarrow{AF}=\overrightarrow{AG}-\overrightarrow{AD}\).

\(\Rightarrow \overrightarrow{AF}=\overrightarrow{DG}\).

Vậy F là đỉnh của hình bình hành ADGF.

Cho hình tứ diện ABCD. Gọi G là trọng tâm tam giác ABC. Chứng minh rằng: \(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=3\overrightarrow{DG}.\)

Phương pháp giải:

Chứng minh VT = VP bằng cách áp dụng quy tắc ba điểm và công thức trọng tâm.

Hướng dẫn giải:

Ta có:

\(\overrightarrow{DA}=\overrightarrow{DG}+\overrightarrow{GA}\)

\(\overrightarrow{DB}=\overrightarrow{DG}+\overrightarrow{GB}\)

\(\overrightarrow{DC}=\overrightarrow{DG}+\overrightarrow{GC}\)

Suy ra \(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=3.\overrightarrow{DG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\).

Mà G là trọng tâm tam giác ABC nên \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).

Vậy \(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=3\overrightarrow{DG}.\)

Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh rằng:

a) \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0};\)

b) \(\overrightarrow{PI}=\frac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}).\)

Phương pháp giải:

a) Chứng minh VT = VP bằng cách áp dụng quy tắc ba điểm và quy tắc trung điểm.

b) Sử dụng đẳng thức ở câu a, quy tắc ba điểm để chứng minh VT = VP.

Hướng dẫn giải:

a) Ta có: M, N là trung điểm của AC và BD nên

\(\overrightarrow{IA}+\overrightarrow{IC}=2\overrightarrow{IM}\).

\(\overrightarrow{IB}+\overrightarrow{ID}=2\overrightarrow{IN}\).

Cộng từng vế ta được:

\(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=2(\overrightarrow{IM}+\overrightarrow{IN})=\overrightarrow{0}.\) (Vì I là trung điểm của MN nên ta có  \(\overrightarrow{IM}+\overrightarrow{IN}=\overrightarrow{0}\))

b) Ta có:

\(\overrightarrow{PI}=\overrightarrow{PA}+\overrightarrow{AI}\).

\(\overrightarrow{PI}=\overrightarrow{PB}+\overrightarrow{BI}\).

\(\overrightarrow{PI}=\overrightarrow{PC}+\overrightarrow{CI}\).

\(\overrightarrow{PI}=\overrightarrow{PD}+\overrightarrow{DI}\).

Cộng từng vế ta được:

\(4\overrightarrow {PI} = \overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} + (\overrightarrow {AI} + \overrightarrow {BI} + \overrightarrow {CI} + \overrightarrow {DI} )\) (1).

Ở câu a ta có: \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\).

Suy ra \(\overrightarrow{AI}+\overrightarrow{BI}+\overrightarrow{CI}+\overrightarrow{DI}=\overrightarrow{0}.\)

Vậy \(\overrightarrow{PI}=\frac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}).\)

Cho hình lăng trụ tam giác ABC.A′B′C′ có \(\overrightarrow{AA'}=\overrightarrow{a}\), \(\overrightarrow{AB}=\overrightarrow{b}\), \(\overrightarrow{AC}=\overrightarrow{c}\). Hãy phân tích (hay biểu thị) các vectơ \(\overrightarrow{B'C}\), \(\overrightarrow{BC'}\) qua các vectơ \(\overrightarrow{a}, \ \overrightarrow{b}, \ \overrightarrow{c}\).

Phương pháp giải:

Áp dụng quy tắc ba điểm để phân tích  \(\overrightarrow{B'C}\), \(\overrightarrow{BC'}\) theo các vectơ \(\overrightarrow{a}, \ \overrightarrow{b}, \ \overrightarrow{c}\).

Hướng dẫn giải:

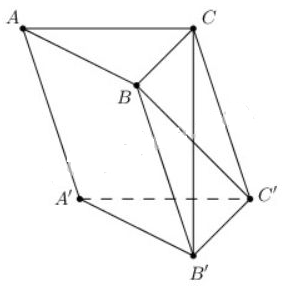
Ta có:

\(\overrightarrow{B'C}=\overrightarrow{B'A'}+\overrightarrow{A'A}+\overrightarrow{AC}\).

Mà \(\overrightarrow{A'A}=-\overrightarrow{AA'}=-\overrightarrow{a}\), \(\overrightarrow{B'A'}=-\overrightarrow{A'B'}=-\overrightarrow{AB}=-\overrightarrow{b}\).

Nên \(\overrightarrow{B'C}=-\overrightarrow{b}-\overrightarrow{a}+\overrightarrow{c}\).

Tương tự ta có:

\(\overrightarrow{BC'}=\overrightarrow{BA}+\overrightarrow{AA'}+\overrightarrow{A'C}\).

Mà \(\overrightarrow{BA}=-\overrightarrow{AB}=-\overrightarrow{b};\overrightarrow{A'C'}=\overrightarrow{AC}=\overrightarrow{c}\).

Nên \(\overrightarrow{BC'}=-\overrightarrow{b} + \overrightarrow{a} + \overrightarrow{c}\)

Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho \(\overrightarrow{MS}=-2\overrightarrow{MA}\) và trên đoạn BC lấy điểm N sao cho \(\overrightarrow{NB}=-\frac{1}{2}\overrightarrow{NC}.\) Chứng minh rằng ba vectơ \(\overrightarrow{AB},\ \overrightarrow{MN},\ \overrightarrow{SC}\) đồng phẳng.

Phương pháp giải:

Biểu diễn \( \overrightarrow{MN}\) theo hai vectơ \(\overrightarrow{AB},\ \overrightarrow{SC}\).

→ Ba vectơ \(\overrightarrow{AB},\ \overrightarrow{MN},\ \overrightarrow{SC}\) đồng phẳng.

Hướng dẫn giải:

Ta có: \(\overrightarrow{MS}=-2\overrightarrow{MA}\) (giả thiết).

\( \Rightarrow MS=2.MA \Rightarrow MS=\frac{2}{3}AS\) và \(\overrightarrow{MS}\) cùng hướng với \(\overrightarrow{AS}\).

\( \Rightarrow\overrightarrow{MS}=\frac{2}{3}\overrightarrow{AS}\).

Lại có: \(\overrightarrow{NB}=-\frac{1}{2}\overrightarrow{NC}\).

\( \Rightarrow NC=2.NB=>CN=\frac{2}{3}CB\) và  \(\overrightarrow{CN}\) cùng hướng với \(\overrightarrow{CB}\).

\( \Rightarrow\overrightarrow{CN}=\frac{2}{3}\overrightarrow{CB}.\)

Do đó:

\(\overrightarrow {MN} = \overrightarrow {MS} + \overrightarrow {SC} + \overrightarrow {CN} = \frac{2}{3}\overrightarrow {AS} + \overrightarrow {SC} + \frac{2}{3}\overrightarrow {CB} \) (1).

\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} = -\frac{1}{3}\overrightarrow {AS} + \overrightarrow {AB} -\frac{1}{3}\overrightarrow {CB} \) (2).

Nhân (2) với 2 rồi cộng với (1) ta được:

\(3\overrightarrow{MN}=\overrightarrow{SC}+2\overrightarrow{AB}\Leftrightarrow\overrightarrow{MN}= \frac{1}{3}\overrightarrow{SC}+\frac{2}{3}\overrightarrow{AB}.\)

Vậy ba vectơ \(\overrightarrow{AB},\ \overrightarrow{MN},\ \overrightarrow{SC}\) đồng phẳng.

Cho hình hộp ABCD.EFGH. Gọi K là giao điểm của AH và DE, I là giao điểm của BH và DF. Chứng minh ba véctơ \(\overrightarrow{AC},\ \overrightarrow{KI},\ \overrightarrow{FG}\) đồng phẳng.

Phương pháp giải:

Chứng minh giá của các véctơ \( \overrightarrow{KI},\ \overrightarrow{FG}\) song song với mặt phẳng (ABCD) chứa véctơ \(\overrightarrow{AC}\).

→ Ba véctơ \(\overrightarrow{AC},\ \overrightarrow{KI},\ \overrightarrow{FG}\) đồng phẳng.

Hướng dẫn giải:

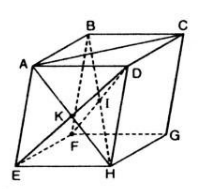
Ta có:

I là giao điểm của BH và DF nên I là trung điểm của BH (1).

K là giao điểm của AH và DE nên K là trung điểm của AH (2).

Từ (1) và (2) suy ra KI là đường trung bình của tam giác ABH. Do đó KI // AB.

\( \Rightarrow\) KI // (ABCD) (3).

Lại có BCGF là hình bình hành nên FG // BC.

\( \Rightarrow\) FG // (ABCD) (4).

Từ (3) và (4) suy ra \(\overrightarrow{AC},\ \overrightarrow{KI},\ \overrightarrow{FG}\) đồng phẳng.

\(\overrightarrow{MA} +\overrightarrow{MB}= 2\overrightarrow{MI}\) với M là một điểm bất kì trong không gian và I là trung điểm của AB.