Giải bài tập SBT Toán 12 Bài 3: Khái niệm về thể tích khối đa diện

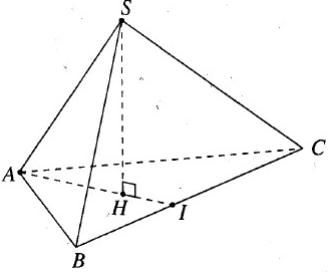
Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc 60^o. Hãy tính thể tích của khối chóp đó.

Phương pháp giải

- Tính chiều cao và diện tích tam giác đáy.

- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\)

Hướng dẫn giải

Kẻ \(SH \bot (ABC)\). Đường thẳng AH cắt BC tại I.

Do S.ABC là hình chóp tam giác đều nên H là trọng tâm của \(\Delta ABC\) nên I là trung điểm BC.

Nên AI vừa là trung tuyến vừa là đường cao trong tam giác.

Tam giác ABI vuông tại I có \(AB = a,BI = \frac{a}{2}\)

Theo Pitago ta có: \(AI = \sqrt {A{B^2} - B{I^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)

Do đó \(AH = \frac{2}{3}AI= \dfrac{2}{3}.\frac{{a\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{3}a,\)

Ta có: \(SH \bot \left( {ABC} \right)\) nên AH là hình chiếu của SA trên mp(ABC)

Do đó góc giữa SA và (ABC) là góc giữa SA và AH hay \(\widehat {SAH} = {60^0}\)

Tam giác SAH vuông tại H có \(SH = AH.\tan {60^0} = \dfrac{{\sqrt 3 }}{3}a.\sqrt 3 = a\)

Thể tích khối chóp S.ABC là:

\(V = \frac{1}{3}SH.{S_{ABC}}= \frac{1}{3}SH.\frac{1}{2}AI.BC\) \( = \frac{1}{3}.a.\frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a= \dfrac{{\sqrt 3 }}{{12}}{a^3}\)

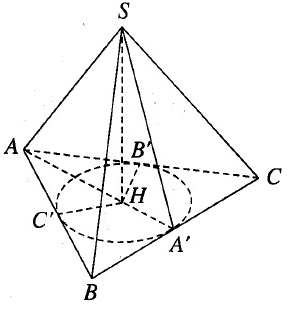
Cho khối chóp S.ABC có đáy là tam giác cân, AB = AC = 5a, BC = 6a và các mặt bên tạo với đáy một góc 60o. Hãy tính thể tích của khối chóp đó.

Phương pháp giải

- Dựng hình chiếu của S trên mặt đáy, từ đó xác định góc giữa các mặt bên và mặt đáy.

- Tính diện tích đáy, chiều cao dựa vào các kiến thức hình học đã biết.

- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\)

Hướng dẫn giải

Kẻ SH ⊥ (ABC) và HA’, HB’ , HC’ lần lượt vuông góc với BC, CA, AB. Theo định lí ba đường vuông góc ta có SA′ ⊥ BC, SB′ ⊥ CA, SC′ ⊥ AB

Từ đó suy ra \(\widehat {SA'H} = \widehat {SB'H} = \widehat {SC'H} = {60^0}\)

Do đó các tam giác vuông SHA’ , SHB’ , SHC’ bằng nhau. Từ đó suy ra HA’ = HB’ = HC’ . Vậy H là tâm đường tròn nội tiếp tam giác ABC. Do tam giác cân ở A nên AH vừa là đường phân giác , vừa là đường cao, vừa là đường trung tuyến. Từ đó suy ra A, H, A’ thẳng hàng và A’ là trung điểm của BC.

Do đó, AA’² = AB² – BA’² = 25a² – 9a² = 16a²

Vậy AA’ = 4a

Gọi p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp của nó.

Ta có: \(p = \frac{{AB + BC + CA}}{2}= \frac{{5a + 6a + 5a}}{2} = 8a\)

\({S_{ABC}} = \frac{1}{2}AA'.BC = \frac{1}{2}.4a.6a = 12{a^2}\)

Lại có \({S_{ABC}} = pr \Rightarrow 12{a^2} = 8a.r\Rightarrow r = \dfrac{3}{2}a\)

Tam giác SHA' vuông tại H có \(SH = HA'.\tan {60^0} = \dfrac{{3a}}{2}\sqrt 3 = \dfrac{{3\sqrt 3 }}{2}a\)

Thể tích khối chóp là \(V = \frac{1}{3}{S_{ABC}}.SH= \dfrac{1}{3}.12{a^2}.\dfrac{{3\sqrt 3 }}{2}a = 6\sqrt 3 {a^3}\)

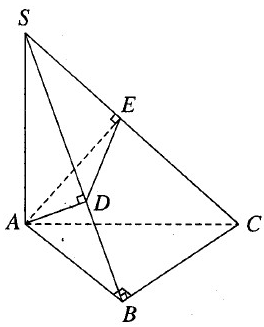
Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c.

a) Hãy tính thể tích khối chóp S.ADE

b) Tính khoảng cách từ E đến mặt phẳng (SAB).

Phương pháp giải

a)

- Chứng minh \(SE \bot \left( {ADE} \right)\)

- Tính diện tích tam giác ADE và chiều cao SE.

- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\)

b) 

- Tính diện tích tam giác SAD.

- Sử dụng công thức \({V_{SADE}} = \dfrac{1}{3}d.{S_{SAD}}\) và kết quả câu a để suy ra d.

Hướng dẫn giải

a) Ta có \(\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AB}\end{array}} \right. \Rightarrow BC \bot (SAB)\)

Vì \(AD \subset (SAB)\) nên \(AD \bot BC\)

Mặt khác \(AD \bot SB\) nên \(AD \bot (SBC)\)

Từ đó suy ra \(AD \bot SC\)

\(\left\{ {\begin{array}{*{20}{c}}{SC \bot AE}\\{SC \bot AD}\end{array}} \right. \Rightarrow SC \bot (ADE) \Rightarrow SC \bot DE\) hay \(SE \bot (ADE)\)

Trong tam giác vuông SAB ta có: \(SA.AB = AD.SB \Rightarrow AD = \dfrac{{AB.SA}}{{SB}} = \dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}\)

Tương tự, trong tam giác vuông SAC ta có: \(AE = \dfrac{{SA.AC}}{{SC}} = \dfrac{{c\sqrt {{a^2} + {b^2}} }}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Do \(AD \bot (SBC)\)  nên \(AD \bot DE\). Từ đó suy ra:

\(DE = \sqrt {A{E^2} - A{D^2}} \)\( = \sqrt {\dfrac{{{c^2}({a^2} + {b^2})}}{{{a^2} + {b^2} + {c^2}}} - \dfrac{{{a^2}{c^2}}}{{{a^2} + {c^2}}}} \) \( = \dfrac{{{c^2}b}}{{\sqrt {({a^2} + {b^2} + {c^2})({a^2} + {c^2})} }}\)

\(SE = \sqrt {S{A^2} - A{E^2}} \)\( = \sqrt {{c^2} - \dfrac{{{c^2}({a^2} + {b^2})}}{{{a^2} + {b^2} + {c^2}}}} \) \( = \dfrac{{{c^2}}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Vậy

\({V_{S.ADE}} = \dfrac{1}{3}.\dfrac{1}{2}AD.DE.SE\)\( = \dfrac{1}{6}\dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}.\dfrac{{{c^2}b}}{{\sqrt {({a^2} + {b^2} + {c^2})({a^2} + {c^2})} }}.\dfrac{{{c^2}}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

\(= \dfrac{{ab{c^5}}}{{6({a^2} + {b^2} + {c^2})({a^2} + {c^2})}}\)

b) 

Gọi d là khoảng cách từ E đến mặt phẳng \(\left( {SAB} \right)\)

Ta có: \(SD = \sqrt {S{A^2} - A{D^2}} \)\( = \sqrt {{c^2} - \dfrac{{{a^2}{c^2}}}{{{a^2} + {c^2}}}} = \dfrac{{{c^2}}}{{\sqrt {{a^2} + {c^2}} }}\)

\({V_{S.ADE}} = {V_{E.SAD}}\)\( = \dfrac{1}{3}.\dfrac{1}{2}SD.AD.d\) \( = \dfrac{1}{6}.\dfrac{{{c^2}}}{{\sqrt {{a^2} + {c^2}} }}.\dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}.d\) \( = \dfrac{1}{6}.\dfrac{{a{c^3}}}{{{a^2} + {c^2}}}.d\)

Kết hợp với kết quả trong câu a ta suy ra \(d = \dfrac{{b{c^2}}}{{{a^2} + {b^2} + {c^2}}}\)

Chứng minh rằng tổng các khoảng cách từ một điểm bất kì trong một tứ diện đều đến các mặt phẳng của nó là một số không đổi.

Phương pháp giải

- Tính thể tích mỗi khối chóp đỉnh M và đáy là các tam giác đều.

- Tính tổng thể tích và suy ra tổng khoảng cách từ M đến các mặt bên.

Hướng dẫn giải

Ta có tứ diện đều ABCD, M là một điểm trong của nó. Gọi V là thể tích, S là diện tích mỗi mặt của tứ diện đều ABCD, hA, hB, hC, hD lần lượt là khoảng cách từ M đến các mặt (BCD), (CDA), (DAB), (ABC).

Ta có:

\({V_{M.BCD}} = \dfrac{1}{3}S{h_A},{V_{M.CDA}} = \dfrac{1}{3}S{h_B},\) \({V_{M.DAB}} = \dfrac{1}{3}S{h_C},{V_{M.ABC}} = \dfrac{1}{3}S{h_D}\)

Khi đó ta có:

\(V = {V_{MBCD}} + {V_{MCDA}} + {V_{MDAB}} + {V_{MABC}}\)\( = \dfrac{1}{3}S\left( {{h_A} + {h_B} + {h_C} + {h_D}} \right)\)

\(\Rightarrow {h_A} + {h_B} + {h_C} + {h_D} = \dfrac{{3V}}{S}\)

Mà V, S là các số không đổi nên \({h_A} + {h_B} + {h_C} + {h_D}\) không đổi. (đpcm)

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD.

a) Tính thể tích khối chóp M.AB’C

b) Tính khoảng cách từ M đến mặt phẳng (AB’C).

Phương pháp giải

a) 

- Đổi vị trí đỉnh và đáy của khối chóp, đưa về khối chóp có chiều cao và đáy dễ tính toán.

- Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\)

b) 

- Tính diện tích tam giác AB'C

- Dựa vào thể tích và diện tích của khối chóp M.AB'C suy ra khoảng cách theo công thức \(h = \dfrac{{3V}}{S}\)

Hướng dẫn giải

a) 

Ta có: \({V_{M.AB'C}} = {V_{B'.ACM}}\)

\({S_{AMC}} = \dfrac{3}{4}{S_{ADC}} = \dfrac{3}{4}.\dfrac{1}{2}.2{a^2} = \dfrac{{3{a^2}}}{4}\)

Do đó \({V_{M.AB'C}} = {V_{B'.ACM}} = \dfrac{1}{3}B'B.{S_{AMC}} = \dfrac{1}{3}.\dfrac{{3{a^2}}}{4}.a = \dfrac{{{a^3}}}{4}\)

b) 

Gọi h là khoảng cách từ M đến mặt phẳng \(\left( {AB'C} \right)\)

Khi đó \({V_{M.AB'C}} = \dfrac{1}{3}{S_{AB'C}}.h = \dfrac{{{a^3}}}{4}\)

Vì \(A{C^2} = {\rm{ }}B'{C^2} = 5{a^2}\) nên tam giác ACB' cân tại C. Do đó, đường trung tuyến CI của tam giác ACB' cũng là đường cao.

Ta có:

\(C{I^2} = {\rm{ }}C{A^2}-{\rm{ }}A{I^2}\)\( = {\rm{ }}5{a^2} - {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2}\) \( = 5{a^2} - \dfrac{{{a^2}}}{2} = \dfrac{{9{a^2}}}{2}\)

Do đó

\(CI = \dfrac{{3a}}{{\sqrt 2 }}\)\( \Rightarrow {S_{AB'C}} = \dfrac{1}{2}.\dfrac{{3a}}{{\sqrt 2 }}.a\sqrt 2 = \dfrac{{3{a^2}}}{2}\)

\(\Rightarrow h = \dfrac{{3V}}{S} = \dfrac{{3{a^3}}}{4}:\dfrac{{3{a^2}}}{2} = \dfrac{a}{2}\)

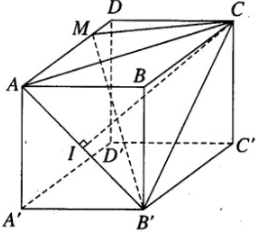
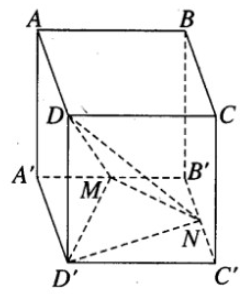
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’

Phương pháp giải

- Đổi vị trí đỉnh và đáy của khối chóp, đưa về khối chóp có chiều cao và đáy dễ tính toán.

- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).

- Tính thể tích khối hộp chữ nhật. Từ đó suy ra tỉ số.

Hướng dẫn giải

Thể tích khối chóp D'.DMN bằng thể tích khối chóp D.D'MN

Ta có:

\(\begin{array}{l} {S_{A'B'C'D'}} = A'B'.B'C'={ab}\\ {S_{D'A'M}} = \frac{1}{2}A'D.A'M = \frac{1}{2}.b.\frac{a}{2} = \frac{{ab}}{4}\\ {S_{B'MN}} = \frac{1}{2}B'M.B'N = \frac{1}{2}.\frac{a}{2}.\frac{b}{2} = \frac{{ab}}{8}\\ {S_{D'C'N}} = \frac{1}{2}C'D'.C'N = \frac{1}{2}.a.\frac{b}{2} = \frac{{ab}}{4} \end{array}\)

\({S_{D'MN}} = {S_{A'B'C'D'}} - \left( {{S_{D'A'M}} + {S_{B'MN}} + {S_{D'C'N}}} \right)\)\( = ab - \left( {\dfrac{{ab}}{4} + \dfrac{{ab}}{8} + \dfrac{{ab}}{4}} \right) = \dfrac{{3ab}}{8}\)

Thể tích khối chóp \({V_{D'.DMN}} = \frac{1}{3}{S_{D'MN}}.DD'= \dfrac{1}{3}.\dfrac{{3ab}}{8}.c = \dfrac{{abc}}{8}\)

Lại có \({V_{ABCD.A'B'C'D'}} = abc\Rightarrow \dfrac{{{V_{D'.DMN}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{8}\)

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho \(BE = \dfrac{1}{2}EB',DF = \dfrac{1}{2}FD'\). Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).

Phương pháp giải

- Tính thể tích các khối đa diện, sử dụng phương pháp phân chia khối đa diện.

- Từ đó suy ra tỉ số.

Hướng dẫn giải

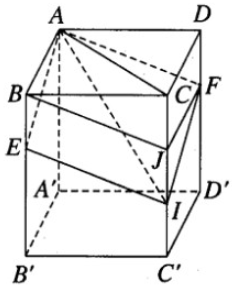
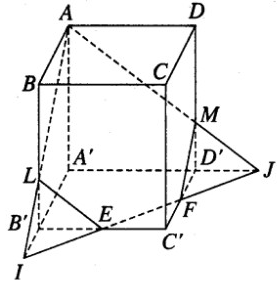
Cho hình hộp ABCD.A’B’C’D’ . Gọi E và F lần lượt là trung điểm của B’C’ và C’D’. Mặt phẳng (AEF) chia hình hộp đó thành hai hình đa diện (H) và (H’), trong đó (H) là hình đa diện chứa đỉnh A’. Tính tỉ số giữa thể tích hình đa diện (H) và thể tích hình đa diện (H’).

Phương pháp giải

- Xác định thiết diện của hình hộp khi cắt bởi \(\left( {AEF} \right)\)

- Đặt thể tích khối hộp ABCD.A'B'C'D' là V

- Tính thể tích khối đa diện ( H ) bằng phương pháp phân chia khối đa diện.

Hướng dẫn giải

Trong \(\left( {A'B'C'D'} \right)\), gọi I, J lần lượt là giao điểm của EF với A'B' và A'D'.

Trong (ADD'A'), gọi \(M = AJ \cap D'D\)

Trong \(\left( {ABB'A'} \right)\), gọi \(L = AI \cap BB'\)

Khi đó thiết diện của hình hộp khi cắt bởi \(\left( {AEF} \right)\) là ngũ giác AMFEL.

Khi đó (H) là khối đa diện chứ đỉnh A' và \({V_{\left( H \right)}} = {V_{A.A'IJ}} - {V_{M.D'JF}} - {V_{L.B'IE}}\)

Gọi V₀ là thể tích khối tứ diện A.A'IJ. V là thể tích khối hộp ABCD.A'B'C'D'.

Vì EB' = EC' và B'I//C'F nên \(B' = FC' = \dfrac{{A'B'}}{2}\)

Do đó \(\dfrac{{IB'}}{{IA'}} = \dfrac{1}{3}\)

Mà BE'//A'J; \(B'L//AA' \Rightarrow \dfrac{{IL}}{{IA}} = \dfrac{{IE}}{{IJ}} = \dfrac{{IB'}}{{IA'}} = \dfrac{1}{3}\)

\(\Rightarrow \dfrac{{{V_{I.ELB'}}}}{{{V_{I.JAA'}}}} = \dfrac{{IL}}{{IA}}.\dfrac{{IE}}{{IJ}}.\dfrac{{LE}}{{AJ}} = {\left( {\dfrac{1}{3}} \right)^3} = \dfrac{1}{{27}}\)

Do đó \({V_{I.ELB'}} = \dfrac{1}{{27}}{V_0}\)

Tương tự \({V_{J.MFD'}} = \dfrac{1}{{27}}{V_0}\)

Gọi A'B' = a,B'C' = b, đường cao hạ từ A xuống (A'B'C'D') là h thì \(IA' = \dfrac{3}{2}A'B' = \dfrac{{3a}}{2};A'J = \dfrac{3}{2}A'D' = \dfrac{{3b}}{2}\) và

\(V = {V_{ABCD.A'B'C'D'}} = {S_{A'B'C'D'}}h = abh.\sin \widehat {B'A'D'}\)

\({V_0} = \dfrac{1}{3}{S_{A'IJ}}.h\) \( = \dfrac{1}{3}.\left( {\dfrac{1}{2}.\dfrac{{3a}}{2}.\dfrac{{3b}}{2}\sin \widehat {B'A'D'}} \right)h\) \( = \dfrac{3}{8}abh.\sin \widehat {B'A'D'}\)

\(\Rightarrow \dfrac{{{V_0}}}{V} = \dfrac{3}{8} \Rightarrow {V_0} = \dfrac{{3V}}{8}\)

Vậy  \({V_{(H)}} = {V_0} - \dfrac{2}{{27}}{V_0} = \dfrac{{25}}{{27}}{V_0} = \dfrac{{25}}{{27}}.\dfrac{{3V}}{8} = \dfrac{{25}}{{72}}V\)

\({V_{(H')}} = V - {V_{\left( H \right)}} = \dfrac{{47}}{{72}}V \Rightarrow \dfrac{{{V_{(H)}}}}{{{V_{(H')}}}} = \dfrac{{25}}{{47}}\)