Giải bài tập SGK Toán 12 Bài 2: Mặt cầu

Tìm tập hợp tất cả các điểm trong không gian luôn luôn nhìn đoạn thẳng \(AB\) cố định dưới một góc vuông.

Phương pháp giải

• Trong tam giác vuông có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
• Tâm đường tròn ngoại tiếp tam giác tam giác vuông là trung điểm của cạnh huyền.

Hướng dẫn giải

Gọi \(O\) là trung điểm đoạn thẳng \(AB\), vì tam giác \(AMB\) vuông tại \(M\) nên trung tuyến \(MO\) bằng nửa cạnh huyền, tức \(MO = {AB\over2} = R\).

Vậy tập hợp các điểm \(M\) nhìn \(AB\) dưới một góc vuông nằm trên mặt cầu đường kính \(AB\)

Ngược lại, lấy \(M\) thuốc mặt cầu đường kính \(AB\) thì \(MO = {AB\over2}\).

Do đó nếu \(M\) khác \(A\) và \(B\)  thì tam giác \(MAB\) vuông tại \(M\), còn khi \(M  \equiv  A\) hoặc \(M \equiv  B\) ta cũng coi \(M\) nhìn \(AB\) một góc vuông.

Kết luận: Tập hợp các điểm \(M\) trong không gian nhìn đoạn thẳng \(AB\) dưới một góc vuông là mặt cầu đường kính \(AB\).

Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng \(a\). Hãy xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.

Phương pháp giải

Sử dụng đính lý Pi-ta-go để tính các cạnh và tìm tâm, tính bán kính của mặt cầu ngoại tiếp khối chóp.

Hướng dẫn giải

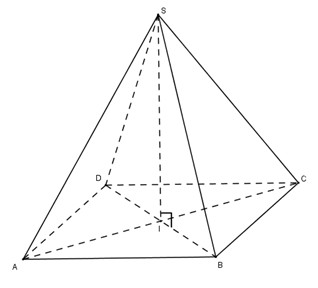
Gọi \(I = AC ∩ BD\). 

Ta có ABCD là hình vuông cạnh \(a\) nên ta có:  \(AC = BD = AB\sqrt 2  = a\sqrt 2 .\)

\(\Delta ASC\) có \(S{A^2} + S{C^2} = {a^2} + {a^2} = 2{a^2} = A{C^2}\) nên là tam giác vuông cân tại \(S\).

Tương tự tam giác SBD cũng vuông cân tại S.

\( \Rightarrow \frac{1}{{S{I^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{C^2}}}\) \( = \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} = \frac{2}{{{a^2}}} \Rightarrow SI = \frac{{a\sqrt 2 }}{2}.\)

\( \Rightarrow IA = IB = IC = ID = IS = \frac{{a\sqrt 2 }}{2}.\)

Vậy mặt cầu ngoại tiếp hình chóp \(SABCD\) có tâm \(I\) và bán kính \(R= \frac{{a\sqrt 2 }}{2}.\)

Tìm tập hợp tâm các mặt cầu luôn luôn chứa một đường tròn cố định cho trước.

Phương pháp giải

Sử dụng các tính chất của mặt cầu để làm bài.

Hướng dẫn giải

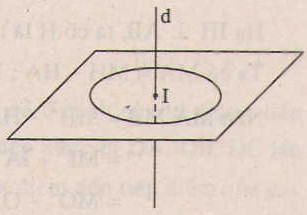
Gọi O là tâm của mặt cầu chứa đường tròn (C) cố định cho trước.

⇒ O cách đều tất cả các điểm M thuộc đường tròn (C)

⇒ O nằm trên đường thẳng đi qua tâm của đường tròn (C) và vuông góc với mặt phẳng chứa (C).

Kết luận: Tập hợp tâm các mặt cầu luôn luôn chứa một đường tròn cố định cho trước là đường thẳng \(d\) vuông góc với mặt phẳng chứa đường tròn tại tâm của nó.

Tìm tập hợp tâm những mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.

Hướng dẫn giải

Giả sử tam giác ABC cho trước nằm trong mặt phẳng (P). mặt cầu (S) tiếp xúc với ba cạnh của tam giác ABC sẽ giao với mặt phẳng (P) theo một đường tròn tiếp xúc với ba cạnh của tam giác ABC, chính là đường tròn nội tiếp tam giác ABC.

Theo bài 3, tập hợp tâm các mặt cầu luôn tiếp xúc với ba cạnh của tam giác  ABC là trục đường tròn nội tiếp tam giác ABC

Từ một điểm M nằm nằm bên ngoài mặt cầu S( O; r) ta kẻ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D.

a) Chứng minh rằng MA>MB = MC>MD.

b) GỌi MO = d. Tính MA>MB theo r và d.

Phương pháp giải

• Sử dụng các tam giác đồng dạng để chứng minh các tỉ lệ giữa các cạnh. Từ đó suy ra tích cần chứng minh.
• Sử dụng định lý Pi-ta-go và tỉ lệ vừa chứng minh ở câu a để tính đại lượng cần tính.

Hướng dẫn giải

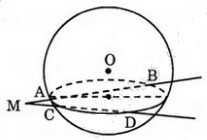
Câu a

Gọi \((P)\) là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng\((P)\) cắt mặt cầu \(S(O;r)\) theo một đường tròn tâm \(I\), là hình chiếu vuông góc của \(O\) lên mặt phẳng \((P)\).

Xét hai tam giác \(MAD\) và \(MCB\) có:

\(\widehat B = \widehat D\) (Hai góc cùng chắn một cung)

\(\widehat M\) chung

\( \Rightarrow \Delta MAD\) đồng dạng với \(\Delta MCB.\)

\(\Rightarrow{{MA} \over {MC}} = {{MD} \over {MB}}\) (các cặp cạnh tương ứng tỉ lệ).

\(\Rightarrow MA.MB=MC.MD \, \, \, (dpcm)\)

Câu b

Đặt \(MO = d\), ta có \(OI\) vuông góc với \((P)\) và ta có:

\(O{M^2} = M{I^2} = O{I^2};O{A^2} = O{I^2} + I{A^2}\)

Hạ \(IH\) vuông góc \(AB\), ta có \(H\) là trung điểm của \(AB\).

Ta có \(MA = MH - HA\); \(MB = MH + HB = MH + HA\).

\(MA.MB = M{H^2} - H{A^2}\) \(= (M{H^2} + H{I^2}) - (H{A^2} + I{H^2})\) \( =M{I^2} - I{A^2} \) \(= (M{I^2} + O{I^2}) - (I{A^2} + O{I^2})\) \(= O{M^2} - O{A^2}\) \(= {d^2} - {r^2}\)

Vậy \(MA.MB = {d^2} - {r^2}\).

Gọi mặt cầu \(S(O; r)\) tiếp xúc với \((P)\) tại \(I\). Gọi \(M\) là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với \(I\) qua tâm \(O\). Từ \(M\) kẻ hai tiếp tuyến cắt của mặt cầu cắt \((P)\) tại \(A\) và \(B\). Chứng minh rằng \( \widehat{AMB}= \widehat{AIB}\).

Phương pháp giải

• Áp dụng tính chất của hai tiếp tuyến cắt nhau.
• Chứng minh hai tam giác bằng nhau suy ra các góc tương ứng bằng nhau.

Hướng dẫn giải

Theo tính chất của mặt cầu, ta có AI và AM là hai tiếp tuyến với cầu kẻ từ A, cho nên AI = AM, tương tự BI =BM.

Từ đó hai tam giác ABI và ABM bằng nahau (c.c.c), cho nên các góc tương ứng bằng nhau, tức 

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, AD = c.

a) Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.

b) Tính bán kính của đường tròn là giao tuyến cưa mặt phẳng (ABCD) với mặt cầu trên.

Phương pháp giải

Xác định tâm và bán kính của hình hộp dựa vào tính chất các đường chéo của hình hộp thì bằng nhau

Hướng dẫn giải

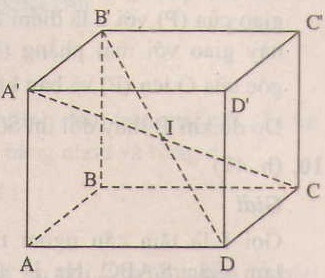
Câu a

Trong hình hộp chữ nhật, bốn đường chéo AC", BD', CA" và DB" căt nhau tại điểm I là trung điểm của mỗi đường.

Vì 4 đường chéo trong hình hộp chữ nhật bằng nhau, nên điểm I cách đề 8 đỉnh của hình hộp chữ nhật. Nó là tâm của mặt cầu ngoại tiếp hình hộp.

Vì AB = b, AD = c, AA' = a nên bán kính mặt cầu\(R=\frac{1}{2}.A'C=\frac{1}{2}.\sqrt{a^2+b^2+c^2}\).

Câu b

Giao tuyến của mặt phẳng ABCD với mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' là hai đwòng tròn ngoại tiếp hình chữ nhật ABCD. Nên bán kính của đường trong giao tuyến là 

\(r=\frac{1}{2}.AC=\frac{1}{2}.\sqrt{b^2+c^2}\)

Chứng minh rắng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì tổng độ dài của các cặp cạnh đối diện tứ diện bằng nhau.

Phương pháp giải

Gọi các tiếp điểm và sử dụng tính chất tiếp tuyến cắt nhau của mặt cầu để chứng minh.

Hướng dẫn giải

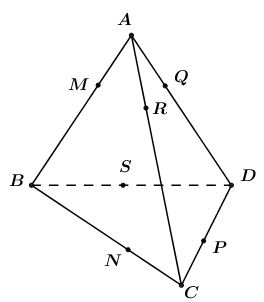
Giả sử tứ diện \(ABCD\) có mặt cầu tiếp xúc với cả \(6\) cạnh của tứ diện; tiếp xúc với \(AB, BC, CD,AD,AC,BD\) lần lượt tại \(M,N,P,Q,R,S\). Vì các đoạn thẳng kẻ từ một điểm đến tiếp điểm của các tiếp tuyến đó bằng nhau, nên ta có:

\( \left\{\begin{matrix} AM= AR = AQ\\ BM= BN= BS\\ CN= CP= CR\\ DP = DQ = DS\\ \end{matrix}\right.\)

Ta chứng minh: \(AB + CD = AC +BD = AD + BC\).

Ta có

\(AM + MB + CP + PD \)\(=AR+RC+BS+SD\)

\(= AQ + QD + BN + NC\)

Hay:  \(AB + CD = AC +BD = AD + BC\)

Cho một điểm \(A\) cố định và một đường thẳng \(a\) cố định không đi qua \(A\). Gọi \(O\) là một điểm thay đổi trên \(a\). Chứng minh rằng các mặt cầu tâm \(O\) và bán kính \(r = OA\) luôn luôn đi qua một đường tròn cố định.

Hướng dẫn giải

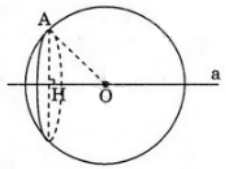
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.

Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.

Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.

Cho hình chóp \(S.ABC\) có bốn đỉnh đếu nằm trên một mặt cầu, \(SA = a, SB = b, SC = c\) và ba cạnh \(SA, SB, SC\) đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo bởi mặt cầu đó.

Phương pháp giải

• Công thức tính diện tích mặt cầu bán kính \(r\) là: \(S=4 \pi r^2.\)
• Công thức tính thể tích mặt cầu bán kính \(r\) là: \(V=\frac{4}{3} \pi r^3.\)

Hướng dẫn giải

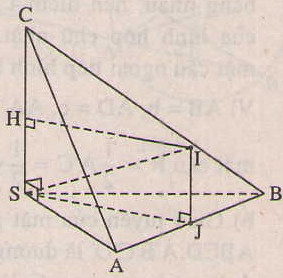
Gọi I là tâm cầu ngoại tiếp hình chóp tam giác S.ABC. Hạ IJ vuông góc (SAB), vì J cách đều 3 điểm S, A, B nên J cũng cách đều 3 điểm S, A, B.

Vì tam giác SAB vuông đỉnh S nên J là trung điểm của AB.

Ta có \(SJ = \frac{1}{2}AB = \frac{1}{2}\sqrt {{a^2} + {b^2}} \).

Do SC vuông góc (SAB) nên IJ // SC.

Gọi H là trung điểm SC, ta có SH = IJ = \(\frac{c}{2}\).

Do vậy, \(IS^2 = IJ^2 + SJ^2 = \frac{(a^2 + b^2 + c^2)}{4}\) và  bán kính hình cầu ngoại tiếp S.ABC là 

\(r=IS=\frac{1}{2}\sqrt{a^2+b^2+c^2}\)

Diện tích mặt cầu là

\(S = 4 \pi r^2 = \pi (a^2 + b^2 + c^2)\) (đvdt)

 Thể tích khối cầu là

 \(V=\frac{4}{3}\pi ^3=\frac{1}{6}\pi (a^2+b^2+c^2)^{\frac{3}{2}}= \frac{1}{6}\pi (a^2+b^2+c^2)\sqrt{a^2+b^2+c^2}\)(đvtt)