Giải bài tập SGK Toán 12 Ôn tập chương 1: Khối đa diện

Các đỉnh, cạnh, mặt của một khối đa diện phải thoả mãn những tính chất nào?

Hướng dẫn giải

Các đỉnh, cạnh, mặt của một khối đa diện phải thoả mãn hai tính chất sau:

• Hai mặt phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
•  Mỗi cạnh của mỗi mặt nào cũng là cạnh chung của đúng hai mặt.

Tìm một hình tạo bởi các đa giác nhưng không phải là một đa diện.

Hướng dẫn giải

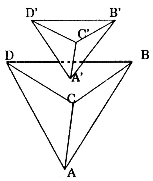
Ở hình vẽ bên, ta xét hình được tạo bởi hai tứ diện ABCD và A'B'C'D'. Đáy không phải là hình đa diện bởi vì hình này không thoả mãn tính chất đầu tiên, đó là:

Hai mặt phân biệt (BCD) và (A'B'C) có điểm chung là A' nhưng không có một đỉnh chung nào và cũng không có một cạnh chung nào.

Thế nào là một khối đa diện lồi. Tìm ví dụ trong một khối đa diện lồi, một khối đa diện không lồi.

Hướng dẫn giải

Cho khối đa diện (H), (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H).

Ví dụ trong thực tế về khối đa diện lồi.

Các khối đa diện lồi trong thực tế như: Bao diêm, hộp phần

Ví dụ về khối đa diện không lồi trong thực tế: Cái tủ lệch (không có chân)

Cho hình lăng trụ và hình chóp có cùng diện tích đáy và chiều cao bằng nhau. Tính tỉ số thể tích của chúng.

Phương pháp giải

Thể tích khối lăng trụ: \(V = B.h\), trong đó \(B\) là diện tích đáy, \(h\) là chiều cao khối lăng trụ.

Thể tích khối chóp: \(V = \dfrac{1}{3}B'.h'\), trong đó \(B'\) là diện tích đáy, \(h'\) là chiều cao khối lăng trụ.

Hướng dẫn giải

Gọi V1, V2 lần lượt là thể tích của một khối lăng trụ và khối chóp.

Gọi S, h lần lượt là diện tích đáy và chiều cao của cả khối lăng trụ và khối chóp.  Theo công thức ta có:

\(V_1=S.h; V_2=\frac{1}{3}S.h\)

Từ đó ta có: \(\frac{V_1}{V_2}=\frac{S.h}{\frac{1}{3}S.h}=3\)

Vậy tỉ số thể tích khối lăng trụ và khối chóp có cùng diện tích đáy và chiều cao là 3.

Cho hình chóp tam giác O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Hãy tính đường cao OH của hình chóp

Phương pháp giải

• Gọi \(H\) là trọng tâm của \(\Delta{ABC}\), chứng minh \(OH \bot (ABC)\).
• Sử dụng các hệ thức lượng trong tam giác vuông tính \(OH\).

Hướng dẫn giải

Gọi I là hình chiếu của O lên AB. Vì OC vuông góc với OA và OB nên \(OC\perp (OAB)\Rightarrow OC\perp AB\).

Từ đó ta suy ra: \(AB\perp (COI)\).

Vậy H là hình chiếu của O lên CI.

Trong tam giác vuông AOB ta có:

\(\frac{1}{OI^2}=\frac{1}{OA^2}+\frac{1}{OB^2} \ \ \ (1)\)

Trong tam giác vuông COI ta có: \(\frac{1}{OH^2}=\frac{1}{OI^2}+\frac{1}{OC^2} \ \ (2)\)

Từ (1) và (2) ta có:

\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2} + \frac{1}{OC^2} \)

\(= \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)

\(=\frac{a^2b^2+b^2c^2+c^2a^2}{a^2b^2c^2}\)

\(\Leftrightarrow OH=\frac{abc}{\sqrt{a^2b^2+b^2c^2+c^2a^2}}\)

Nhận xét: Ta có thể tính OH từ mối liên hệ:

\(V_{O.ABC}=\frac{1}{6}abc=\frac{1}{3}.OH.S_{\Delta ABC}\)

Cho hình chóp tam giác đều \(S.ABC\) có cạnh \(AB\) bằng \(a\). Các cạnh bên \(SA, SB, SC\) tạo với đáy một góc \(60^0\). Gọi \(D\) là giao điểm của \(SA\) với mặt phẳng qua \(BC\) và vuông góc với \(SA\).

a) Tính tỉ số thể tích của hai khối chóp S.DBC và S.ABC

b) Tính thể tích khối chóp S.DBC

Phương pháp giải

• Hình chóp có các cạnh bên tạo với đáy góc bằng nhau thì chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.
• Sử dụng công thức tỉ số thể tích: \(\dfrac{{{V_{S.DBC}}}}{{{V_{S.ABC}}}} = \dfrac{{SD}}{{SA}}.\dfrac{{SB}}{{SB}}.\dfrac{{SC}}{{SC}} = \dfrac{{SD}}{{SA}}\).

Câu a

Ta có: AB = BC = CA = a

Gọi O là hình chiều vuông góc của (S) lên (ABC)

Khi đó ta có: \(\widehat{SBO}=\widehat{SCO}=\widehat{SAO}=60^0\)

\(\Rightarrow \Delta SOA=\Delta SOB=\Delta SOC\)

\(\Rightarrow OA=OB=OC\) hay O là tâm của tam giác đều ABC.

Trong các tam giác SOA, SOB, SOC. Ta có:

\(SA=SB=SC=2OA=2.\frac{2}{3}.\frac{a\sqrt{3}}{2}\)

\(=\frac{2a\sqrt{3}}{3}\)

\(SO=\sqrt{SB^2-OB^2}=a\)

Gọi I là trung điểm của BC, ta có: \(ID\perp SA\)

Nên \(ID. SA=SO.IA\)

\(\Rightarrow ID=\frac{a.\frac{a\sqrt{3}}{2}}{\frac{2a\sqrt{3}}{3}}= \frac{3}{4}a\)

Xét tam giác vuông IDA, ta có:

\(DA=\sqrt{IA^2-ID^2}=\frac{a\sqrt{3}}{4}\)

\(\Rightarrow SD=\frac{2a\sqrt{3}}{3}- \frac{a\sqrt{3}}{4}=\frac{5a\sqrt{3}}{12}\)

Mặt khác: 

\(\frac{V_{S.ABC}}{V_{S.DBC}}=\frac{V_{S.DBC}+V_{A.BCD}}{V_{SDBC}}= 1+\frac{AD}{SD}\)

\(=1+\frac{\frac{a\sqrt{3}}{4}}{\frac{5a\sqrt{3}}{12}}=\frac{8}{5}\Rightarrow \frac{V_{S.DBC}}{V_{S.ABC}}=\frac{5}{8}\)

Câu b

Ta có: \({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4};SH = AH.\tan {60^0} = a\)

\( \Rightarrow {V_{SABC}} = \frac{1}{3}.SH.{S_{ABC}} = \frac{1}{3}.a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{12}}\)

Từ kết quả câu a) ta có:

\({V_{S.DBC}} = \frac{5}{8}.{V_{S.ABC}} = \frac{5}{8}.\frac{{{a^3}\sqrt 3 }}{{12}} = \frac{{5{a^3}\sqrt 3 }}{{96}}\)

Cho hình chóp tam giác \(S.ABC\) có \(AB = 5a, BC = 6a, CA = 7a\). Các mặt bên \(SAB, SBC, SCA\) tạo với đáy một góc \(60^0\). Tính thể tích của khối chóp đó.

Phương pháp giải

Hình chóp có các cạnh bên tạo với đáy các góc bằng nhau có hình chiếu của đỉnh trùng với tâm đường tròn nội tiếp đáy.

Áp dụng công thức tính thể tích \({V_{chóp}} = \dfrac{1}{3}Sh\) trong đó \(S\) là diện tích đáy và \(h\) là chiều cao của khối chóp.

Hướng dẫn giải

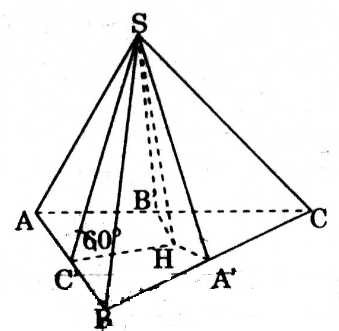
Gọi H là hình chiếu của S lên mặt phẳng (ABC). Gọi A', B', C' lần lượt là hình chiếu của H lên các cạnh BC, CA, AB. Xét các tam giác vuông: SHA', SHB', SHC' có:

\(\widehat{SA'H}=\widehat{SB'H}=\widehat{SC'H}=60^0\) (vì các góc này chính là các góc của mặt bên và mặt đáy ABC)

Từ các tam giác vuông đó dễ dàng suy ra \(SC'=SA'=SB'\) nên HA' = HB'= HC' ⇒ H là tâm đường tròn nội tiếp tam giác ABC.

Mặt khác diện tích của tam giác ABC có thể tính theo công thức:

\(S_{\Delta ABC}=\sqrt{p(p-AB)(p-AC)(p-BC)}\)

Với \(p=\frac{AB+AC+BC}{2}=\frac{5a+6a+7a}{2}=9a\)

Do đó: 

\(S_{\Delta ABC}=\sqrt{(9a-5a)(9a-6a)(9a-7a)p}\)

\(=\sqrt{216a^4}=6a^2\sqrt{6}\)

Vì \(S_{\Delta ABC}=p.r\) (r là bán kính đường tròn nội tiếp tam giác ABC)

\(\Rightarrow r=\frac{6a^2\sqrt{6}}{9a}=\frac{2a\sqrt{6}}{3}\)

Xét tam giác vuông SHA', ta có: \(tan 60^0=\frac{SH}{HA'}\Rightarrow SH=r.tan60^0\)

\(\Rightarrow SH=\frac{2a\sqrt{6}}{3}.\sqrt{3}=2\sqrt{2}a\)

Do đó thể tích của khối chóp S.ABC là:

\(V_{S.ABC}=\frac{1}{3}S._{\Delta ABC}.SH\)

\(=\frac{1}{3}.6.a^2\sqrt{6}. 2\sqrt{2}a=8\sqrt{3}a^3\)

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA\) vuông góc với đáy và \(AB = a, AD = b, SA =c\). Lấy các điểm \(B', D'\) theo thứ tự thuộc \(SB, SD\) sao cho \(AB'\) vuông góc với \(SB, AD'\) vuông góc với \(SD\). Mặt phẳng \((AB'D')\) cắt \(SC\) tại \(C'\). Tính thể tích khối chóp \(S.AB'C'D'\).

Phương pháp giải

Chứng minh \(\displaystyle SC \bot (AB'C'D')\)

\(\displaystyle \Rightarrow V_{S.AB'C'D'} = {{1} \over {3}} SC'.S_{AB'C'D'}\)

Hướng dẫn giải

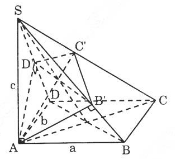
Ta có \(BC \bot AB,BC \bot SA \Rightarrow BC \bot \left( {SAB} \right)\) \(\Rightarrow BC\bot AB'\)

Theo giả thiết \(SB \bot AB'\) \(\Rightarrow AB' \bot (SBC) \Rightarrow AB' \bot SC\)  (1)

Chứng minh tương tự ta có: \(AD' \bot SC\)(2)

Từ (1) và (2) suy ra \(SC \bot (AB'C'D')\) hay \(SC' \bot (AB'C'D')\)

Do đó \(SC'\) là đường cao của hình chóp \(S.AB'C'D'\).

Từ \(AB' \bot (SBC)\) \( \Rightarrow AB' \bot B'C'\)

Tương tự ta có: \(AD' \bot D'C'\)

\( \Rightarrow {S_{AB'C'D'}} = {S_{AB'C'}} + {S_{AD'C'}} \)

\(= \dfrac{1}{2}AB'.B'C' + \dfrac{1}{2}AD'.D'C'\) \( = \dfrac{1}{2}\left( {AB'.B'C' + AD'.D'C'} \right)\)

Từ các kết quả trên, ta được:

\(\displaystyle{V_{AB'C'D'}} = {1 \over 3}.SC'.{1 \over 2}(AB'.B'C' + AD'.D'C')\)

\(\displaystyle ={1 \over 6}SC'.(AB'.B'C' + AD'.D'C')\)     (*)

Ta tính các yếu tố trên.

Tam giác vuông \(SAB\) có \(AB'\) là đường cao, nên ta có:

\(\displaystyle{1 \over {AB{'^2}}} = {1 \over {{a^2}}} + {1 \over {{c^2}}} \Rightarrow AB{'^2} = {{{a^2}{c^2}} \over {{a^2} + {c^2}}}\) \( \displaystyle \Rightarrow AB' = {{ac} \over {\sqrt {{a^2} + {c^2}} }}\)

Tương tự, ta có:

\(\displaystyle AD{'^2} = {{{b^2}{c^2}} \over {{b^2} + {c^2}}} \Rightarrow AD' = {{bc} \over {\sqrt {{b^2} + {c^2}} }}\)

Ta lại có: \(SC^2 = AC^2 + AS^2 = a^2 + b^2 + c^2 \Rightarrow SC = \sqrt {{a^2} + {b^2} + {c^2}} \)

Trong tam giác vuông \(SAC, AC'\) là đường cao

\(\Rightarrow SC'.SC = SA^2\) \( \displaystyle \Rightarrow SC' = {{S{A^2}} \over {SC}} = {{{c^2}} \over {\sqrt {{a^2} + {b^2} + {c^2}} }}\)

\(∆SBC\) đồng dạng  \(∆SC'B'\) (g.g)\( \displaystyle \Rightarrow {{B'C'} \over {BC}} = {{SC'} \over {SB}}\)

\(\displaystyle \Rightarrow B'C' = {{SC'.BC} \over {SB}} = {{b{c^2}} \over {\sqrt {{a^2} + {c^2}} \sqrt {{a^2} + {b^2} + {c^2}} }}\)

Tương tự ta có:  \(\displaystyle D'C' = {{{c^2}a} \over {\sqrt {{b^2} + {c^2}} \sqrt {{a^2} + {b^2} + {c^2}} }}\)

Thay các kết quả này vào (*) ta được:

\(\displaystyle V = {1 \over 6}.{{ab{c^5}({a^2} + {b^2} + 2{c^2})} \over {({a^2} + {c^2})({b^2} + {c^2})({a^2} + {b^2} + {c^2})}}\)

Cho hình chóp tứ giác đều \(S.ABCD\), đáy là hình vuông cạnh \(a\), cạnh bên tạo với đáy một góc \(60^0\). Gọi \(M\) là trung điểm \(SC\). Mặt phẳng đi qua \(AM\) và song song với \(BD\), cắt \(SB\) tại \(E\) và cắt \(SD\) tại \(F\). Tính thể tích khối chóp \(S.AEMF\).

Phương pháp giải

Hình chóp đều có chân đường cao trùng với tâm của đáy.

Xác định thiết diện của hình chóp cắt bởi mặt phẳng đi qua AM và song song với BD là tức giác AEMF.

Chứng minh AEMF có hai đường chéo vuông góc \( \Rightarrow {S_{AEMF}} = \dfrac{1}{2}AM.EF\)

Chứng minh \(SM \bot \left( {AEMF} \right)\) \( \Rightarrow {V_{S.AEMF}} = \dfrac{1}{3}SM.{S_{AEMF}}\)

Hướng dẫn giải

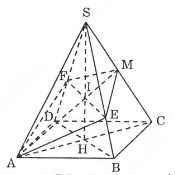
Gọi \(\displaystyle H = AC \cap BD\).

Hình chóp \(\displaystyle S.ABCD\) là hình chóp đều nên chân \(\displaystyle H\) của đường cao \(\displaystyle SH\) chính là tâm của đáy.

Mặt phẳng đi qua \(\displaystyle AM\) và song song với \(\displaystyle BD\) cắt mặt phẳng \(\displaystyle (SDB)\) theo một giao tuyến song song với \(\displaystyle BD\)\. Ta dựng giao tuyến \(\displaystyle EF\) như sau: Gọi \(\displaystyle I\) là giao điểm của \(\displaystyle AM\) và \(\displaystyle SH\). Qua \(\displaystyle I\) ta dựng một đường thẳng song song với \(\displaystyle BD\), đường này cắt \(\displaystyle SB\) ở \(\displaystyle E\) và cắt \(\displaystyle SD\) ở \(\displaystyle F\).

Ta có: \(\displaystyle HA\) là hình chiếu vuông góc của \(\displaystyle SA\) trên \(\displaystyle (ABCD)\) \(\displaystyle \Rightarrow \widehat {\left( {SA;\left( {ABCD} \right)} \right)} = \widehat {\left( {SA;AH} \right)} = \widehat {SAH} = {60^0}\)

Tam giác cân \(\displaystyle SAC\) có \(\displaystyle SA = SC\) và góc \(\displaystyle SAC = 60^0\) nên nó là tam giác đều: \(\displaystyle I\) là giao điểm của các trung tuyến \(\displaystyle AM\) và \(\displaystyle AH\) nên I là trọng tâm của tam giác đều SAC \(\displaystyle \Rightarrow {{SI} \over {SH}} = {2 \over 3}\)

Do \(\displaystyle EF // DB \) \(\displaystyle \Rightarrow {{{\rm{EF}}} \over {DB}} = {{SF} \over {SD}} = {{SE} \over {SB}} = {{SI} \over {SH}} = {2 \over 3}\)

Vì \(\displaystyle DB = a\sqrt2\) \(\displaystyle  \Rightarrow {\rm{EF}} = {{2a\sqrt 2 } \over 3}\)

Tam giác \(\displaystyle SAC\) là tam giác đều nên \(\displaystyle AM = {{AC\sqrt 3 } \over 2} = {{a\sqrt 6 } \over 2}\)

Ta lại có \(\displaystyle \left\{ \begin{array}{l}BD \bot AC\\BD \bot SH\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \) \(\Rightarrow BD \bot AM \Rightarrow AM \bot EF\)

Tứ giác \(\displaystyle AEMF\) có hai đường chéo vuông góc với nhau nên có diện tích: \(\displaystyle {S_{AEMF}} = {1 \over 2}{\rm{EF}}.AM = {1 \over 2}.{{2a\sqrt 2 } \over 3}.{{a\sqrt 6 } \over 2} = {{{a^2}\sqrt 3 } \over 3}\)

Mặt khác, tam giác \(\displaystyle ASC\) là tam giác đều, \(\displaystyle M\) là trung điểm của \(\displaystyle SC\) nên \(\displaystyle AM \bot SC\). Ta cũng có \(\displaystyle DB \bot (SAM)\) \(\displaystyle  \Rightarrow  DB \bot SC\) vì \(\displaystyle DB // EF\) nên \(\displaystyle EF \bot SC\). Từ kết quả trên, suy ra \(\displaystyle SM \bot(AEMF)\).

Dễ thấy \(\displaystyle SM = {{a\sqrt 2 } \over 2}\) (do tam giác \(\displaystyle SAC\) đều). Do đó: \(\displaystyle {V_{S.AEMF}} = {1 \over 3}.{{{a^2}\sqrt 3 } \over 3}.{{a\sqrt 2 } \over 2} = {{{a^3}\sqrt 6 } \over {18}}\).

Cho hình lăng trụ đứng tam giác ABC.A'B'C' có tất cả các cạnh đều bằng a.

a) Tính thể tích khối tứ diện A'BB'C

b) Mặt phẳng đi qua A'B' và trọng tâm tam giác ABC cắt AC và BC lần lượt tạ E và F. Tính thể tích hình chóp C.A'B'FE.

Phương pháp giải

a) Gọi \(M\) là trung điểm của \(B'C'\). Chứng minh \(A'M \bot \left( {BCC'B'} \right)\). Áp dụng công thức \({V_{A'BB'C}} = \dfrac{1}{3}A'M.{S_{BB'C}}\).

b) Phân chia và lắp ghép các khối đa diện: \(V = {V_{B'.CEF}} + {V_{B'.A'EC}} = {V_1} + {V_2}\)

Hướng dẫn giải

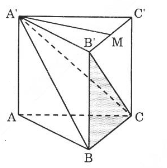
Câu a

Ta tính thể tích hình chóp \(\displaystyle A'.BCB'\).

Gọi \(\displaystyle M\) là trung điểm của \(\displaystyle B'C'\), ta có: \(\displaystyle A'M \bot B'C'\)   (1)

Lăng trụ \(\displaystyle ABC.A'B'C'\) là lăng trụ đứng nên:

\(\displaystyle BB' \bot (A'B'C') \Rightarrow BB' \bot A'M\)   (2)

Từ (1) và (2) suy ra \(\displaystyle A'M \bot (BB'C')\) hay \(\displaystyle A'M\) là đường cao của hình chóp \(\displaystyle A'.BCB'\).

Ta có: \(\displaystyle A'M\) = \(\displaystyle {{a\sqrt 3 } \over 2};{S_{BB'C}} = {1 \over 2}{a^2}\)

\(\displaystyle \Rightarrow {V_{A'BB'C}} = {1 \over 3}.A'M.{S_{BB'C}}\) \( \Rightarrow {V_{A'BB'C}} = {{{a^3}\sqrt 3 } \over {12}}\)

Câu b

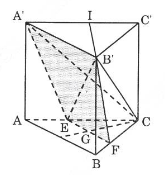
Thể tích hình chóp \(\displaystyle C.A'B'EF\) bằng tổng thể tích hai hình chóp:

- \(\displaystyle V_1\) là thể tích hình chóp đỉnh \(\displaystyle B'\), đáy là tam giác \(\displaystyle CEF\).

- \(\displaystyle V_2\) là thể tích hình chóp đỉnh \(\displaystyle B'\), đáy là tam giác \(\displaystyle A'EC\).

Do \(\displaystyle (ABC) // (A'B'C')\) nên dễ thấy \(\displaystyle EF // AB\). Ta cũng có: \(\displaystyle EF\) = \(\displaystyle {2 \over 3}a\)

Hình chóp \(\displaystyle B'.CEF\) có chiều cao \(\displaystyle BB' = a\) và diện tích đáy là: \(\displaystyle {S_{C{\rm{EF}}}}=\frac{1}{2}EF.CG = {1 \over 2}.{{2a} \over 3}.{2 \over 3}.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 9}\)

Từ đây ta có: \(\displaystyle {V_1} = {{{a^3}\sqrt 3 } \over {27}}\)

Do \(\displaystyle EC = {2 \over 3}AC\) nên \(\displaystyle {S_{A'BE}} = \frac{1}{2}A'A.EC = \frac{1}{2}.a.\frac{2}{3}a = \frac{{{a^2}}}{3}\)

Gọi \(\displaystyle I\) là trung điểm của \(\displaystyle A'C'\) ta có: \(\displaystyle \left\{ \begin{array}{l}B'I \bot A'C\\B'I \bot AA'\end{array} \right. \Rightarrow B'I \bot \left( {ACC'A'} \right) \Rightarrow B'I \bot \left( {A'EC} \right)\)

Hình chóp \(\displaystyle B'.A'EC\) có chiều cao là \(\displaystyle B'I\) bằng \(\displaystyle {{a\sqrt 3 } \over 2}\) nên \(\displaystyle {V_2} = \frac{1}{3}.B'I.{S_{A'EC}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{{{a^2}}}{3} = \frac{{{a^3}\sqrt 3 }}{{18}}\)

Vậy thể tích hình chóp \(\displaystyle C.A'B'FE\) là: \(\displaystyle V = V_1 + V_2\) = \(\displaystyle {{5{a^3}\sqrt 3 } \over {54}}\)

Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(E\) và \(F\) theo thứ tự là trung điểm của các cạnh \(BB'\) và \(DD'\). Mặt phẳng \((CEF)\) chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó.

Phương pháp giải

•  Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (CEF).
• Phân chia và lắp ghép các khối đa diện.

Hướng dẫn giải

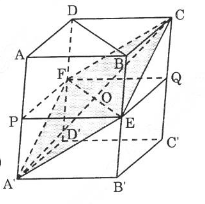
Ta xác định thiết diện của hình hộp \(\displaystyle ABCD.A'B'C'D'\) khi cắt bởi \(\displaystyle (CEF)\). Mặt phẳng \(\displaystyle (CEF)\) chứa đường thẳng \(\displaystyle EF\) mà \(\displaystyle E\) là trung điểm của \(\displaystyle BB', F\) là trung điểm của \(\displaystyle CC'\).

\(\displaystyle O \in EF \Rightarrow O \in (CEF) \Rightarrow CO \subset \left( {CEF} \right)\)

\(\displaystyle A' \in CO \Rightarrow A' \in \left( {CEF} \right)\)

Ta dễ dàng nhận xét rằng thiết diện chính là hình bình hành \(\displaystyle CEA'F\).

Mặt phẳng (CEA'F) chia khối hộp thành 2 phần: ABCD.A'ECF  (\(\displaystyle V_1\)) và A'B'C'D'.CEA'F (\(\displaystyle V_2\))

Qua \(\displaystyle EF\) ta dựng một mặt phẳng song song với đáy hình hộp, mặt phẳng này cắt \(\displaystyle AA'\) ở \(\displaystyle P\) và cắt \(\displaystyle CC'\) ở \(\displaystyle Q\).

Ta có:

\(\displaystyle \begin{array}{l}
{V_{ABCD.A'ECF}} = {V_{ABCD.EFP}} + {V_{A'.PEF}}\\
{V_{A'PEF}} = {V_{C.QEF}}
\end{array}\)

\(\Rightarrow {V_{ABCD.A'ECF}} = {V_{ABCD.EFP}} + {V_{C.QEF}} \) \(= {V_{ABCD.EPFQ}} = \frac{1}{2}V\)

Do đó \(\displaystyle {V_1} = {V_2} = \frac{1}{2}V \Rightarrow \frac{{{V_1}}}{{{V_2}}} = 1\).

Chú ý: Có thể lí luận như sau: Giao điểm \(\displaystyle O\) của các đường chéo của hình hộp là tâm đối xứng của hình hộp, do đó mặt phẳng \(\displaystyle (CEF)\) chứa điểm \(\displaystyle O\) nên chia hình hộp thành hai hình đối xứng với nhau qua điểm \(\displaystyle O\). Vậy hai hình này là hai hình bằng nhau và có thể tích bằng nhau

Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M là trung điểm A'B', N là trung điểm BC.

a) Tính thể tích khối tứ diện BC.

b) Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A, (H) là khối đa diện còn lại. Tính tỉ số \(\frac{V_{(H)}}{V_{(H')}}\)

Phương pháp giải

Sử dụng công thức tính thể tích khối chóp: \({V_{ADMN}} = {V_{M.ADN}} = \frac{1}{3}d\left( {M;\left( {ADN} \right)} \right).{S_{ADN}}\)

Dựng thiết diện của hình lập phương khi cắt bởi mặt phẳng \((DMN)\), xác định hai phần khối đa diện cẩn tính thể tích 

Hướng dẫn giải

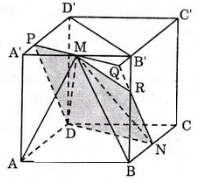
Câu a

Ta tính thể tích hình chóp M.ADN. Hình chóp này có chiều cao bằng a và diện tích AND bằng \(\frac{a^2}{2}\)

\(V_{ADMN}=\frac{1}{3}a.\frac{a^2}{2}=\frac{a^3}{6}\)

Câu b

Trước hết, ta dựng thiết diện của hình lập phương khi cắt bởi mp(DMN).

Do (ABCD) // (A'B'C'D') nên (DMN) cắt (A'B'C'D') theo một giao tuyến song song với DN. Ta dựng thiết diện như sau:

- Từ M kẻ đường thẳng song song với DN, đường này cắt cạnh A'D' tại điểm P và cắt đường thẳng C'B' tại điểm Q. Trong mặt phẳng (BCC'B') thì QN cắt cạnh BB' tại điểm R; đa giác DNRMP chính là thiết diện của hình lập phương khi cắt bởi mp (DMN).

- Bây giờ ta tính thể tích khối đa diện ABNDPMR. Thể tích này có thể coi là thể tích của ba hình chóp.

V1 là thể tích hình chóp đáy ABND, đỉnh M

V2 là thể tích hình chóp đáy AA'PD, đỉnh M

V3 là thể tích hình chóp đáy NRB, đỉnh M

Hình chóp M.ABND, có đường cao bằng a, diện tích đáy là hình thang ABND là:

\(\frac{1}{2}\left ( \frac{a}{2}+a \right ).a=\frac{3a^2}{4}\)

Suy ra: \(V_1=\frac{1}{3}.\frac{3a^2}{4}.a\Rightarrow V=\frac{a^3}{4}\)

Dễ thấy \(A'P=\frac{a}{4}\). Hình chóp M.AA'PD có chiều cao \(\frac{a}{2}\) và diện tích hình thang AA'PD là: \(\frac{1}{2}\left ( \frac{a}{4}+a \right )a=\frac{5a^2}{8}\)

Suy ra: \(V_2=\frac{1}{3}.\frac{a}{2}.\frac{5a^2}{8}\Rightarrow V_2= \frac{5a^2}{48}\)

Dễ thấy \(BR=\frac{2}{3}a\). Diện tích tam giác NRB là: \(\frac{1}{2}.\frac{2}{3}a.\frac{a}{2}=\frac{a^2}{6}\)

Hình chóp M.NRB có chiều cao \(\frac{a}{2}\) và diện tích đáy \(\frac{a^2}{6}\) nên:

\(V_2=\frac{1}{3}.\frac{a}{2}.\frac{a^2}{6}\Rightarrow V_3=\frac{a^3}{36}\)

\(V_{ABNDPMR}=V_1+V_2+V_3\)

\(= \frac{5a^3}{48}+\frac{a^3}{4}+\frac{a^3}{36}=\frac{55a^3}{144}\)

Thể tích phần còn lại là: \(\frac{144a^3}{144}-\frac{55a^3}{144}=\frac{89a^3}{144}\)

Từ đây suy ra tỉ số cần tìm là: \(\frac{55}{89}\)

Trong các mệnh đề sau, mệnh đề nào đúng?

(A) Số đỉnh và số mặt của một hình đa diện luôn bằng nhau;

(B) Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau;

(C) Tồn tại một hình đa diện có số cạnh bằng số đỉnh;

(D) Tồn tại một hình đa diện có số cạnh và mặt bằng nhau.

Hướng dẫn giải

⇒ Chọn đáp án B

Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau. Chẳng hạn khối tứ diện.

Trong các mệnh đề sau, mệnh đề nào đúng?

Số các đỉnh hoặc số các mặt của bất kì hình đa diện nào cũng:

(A) lớn hơn hay bằng 4

(B) lớn hơn 4

(C) lớn hơn hay bằng 5

(D) lớn hơn 5

Hướng dẫn giải

⇒ Chọn đáp án A

Tứ diện có số đỉnh và số mặt bằng 4

Trong các mệnh đề sau, mệnh đề nào đúng?

Số các cạnh của hình đa diện luôn luôn:

(A) Lớn hơn hay bằng 6

(B) Lớn hơn 6

(C) Lớn hơn 7

(D) Lớn hơn hay bằng 8

Hướng dẫn giải

⇒ Chọn đáp án A

Số cạnh của tứ diện là 6.

Trong các mệnh đề sau, mệnh đề nào SAI?

(A) Hình tứ diện là khối đa diện lồi

(B) Hình hộp là khối đa diện lồi

(C) Hình chóp là khối đa diện lồi

(D) Hình lăng trụ tam giác là khối đa diện lồi

Hướng dẫn giải

⇒ Chọn đáp án C

(A), (B), (C) đúng.

Trong các mệnh đề sau, mệnh đề nào SAI?

(A) Hình khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau;

(B) Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau;

(C) Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau;

(D) Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.

Hướng dẫn giải

Chọn đáp án B

(A) (C) (D) đúng.

Cho hình chóp S.ABC. Gọi A', B' lần lượt là trung điểm của SA, SB. Khi đó tỉ số thể tích của hai khối chóp S.A'B'C' và S.ABC là:

(A) \(\frac{1}{2}\)

(B) \(\frac{1}{3}\)

(C) \(\frac{1}{4}\)

(D) \(\frac{1}{8}\)

Hướng dẫn giải

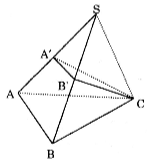
\(\frac{V_{S.A'B'C}}{V_{S.ABC}}=\frac{SA'}{SA}. \frac{SB'}{SB}.\frac{SC'}{SC} =\frac{1}{2}.\frac{1}{2}=\frac{1}{4}\)

⇒ Chọn đáp án C

Cho hình chóp S.ABCD. Gọi A', B', C', D' lần lượt là trung điểm của SA, SB, SC, SD. Tỉ số thể tích của hai khối chóp S.A'B'C'D' và S.ABCD là

(A) \(\frac{1}{2}\)

(B) \(\frac{1}{4}\)

(C) \(\frac{1}{8}\)

(D) \(\frac{1}{16}\)

Hướng dẫn giải

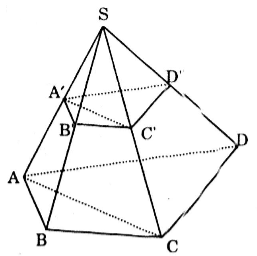
\(\frac{V_{S.A'B'C'}}{V_{S.ABC}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC} =\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1}{8}\)

\(\Rightarrow V_{S.A'B'C'}=\frac{1}{8}V_{S.ABC}\)  (1)

Tương tự: \(V_{S.A'C'D'}=\frac{1}{8}V_{S.ACD}\)  (2)

Lấy (1) cộng (2) ta được:

\(V_{S.A'B'C'D'}=V_{S.A'B'C'}+V_{S.A'C'D'}\)

\(= \frac{1}{8}(V_{S.ABC}+V_{S.ACD})= \frac{1}{8}V_{S.ABCD}\)

Vậy \(\frac{V_{S.A'B'C'D'}}{V}=\frac{1}{8}\)

⇒ Chọn đáp án C

Thể tích khối lăng trụ tam giác đề có tất cả các cạnh bằng a là:

(A) \(\frac{\sqrt{2}}{3}a^3\);

(B) \(\frac{\sqrt{2}}{4}a^3\)

(C) \(\frac{\sqrt{3}}{2}a^3\)

(D) \(\frac{\sqrt{3}}{4}a^3\)

Hướng dẫn giải

\(S_{ABC}=\frac{a^2\sqrt{3}}{4}\Rightarrow V=\frac{a^3\sqrt{3}}{4}\)

⇒ Chọn đáp án D.

Cho hình hộp ABCD.A'B'C'D'. Tỉ số thể tích của khối tứ diện ACB'D' và khối hộp ABCD.A'B'C'D' bằng:

(A) \(\frac{1}{2}\)

(B) \(\frac{1}{3}\)

(C) \(\frac{1}{4}\)

(D) \(\frac{1}{6}\)

Hướng dẫn giải

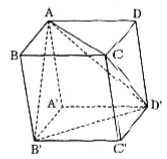
\(V_{ACB'D'}=V_{ABCD.A'B'C'D'}-V_{C.B'C'D'}\)

\(-V_{D'.ACD}-V_{B'.ABC}-V_{A.A'B'D}\) 

\(=V_{AABCD.A'B'C'D'}-\frac{4}{6}V_{ABCD.A'B'C'D'}\)

\(=\frac{1}{3}V\)

⇒ Chọn đáp án B

Cho hình hộp ABCD.A'B'C'D'. Gọi O là giao điểm của AC và BD. Tỉ số thể tích của khối chóp O.A'B'C'D' và khối hộp ABCD.A'B'C'D' bằng:

(A) \(\frac{1}{2}\)

(B) \(\frac{1}{3}\)

(C) \(\frac{1}{4}\)

(D) \(\frac{1}{6}\)

Hướng dẫn giải

\(\frac{V_{O.A'B'C'D'}}{V_{ABCD.A'B'C'D'}}=\frac{\frac{1}{3}S.h}{S.h}=\frac{1}{3}\)

⇒ Chọn đáp án B