Giải bài tập SGK Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Phần hướng dẫn giải bài tập Khảo sát sự biến thiên và vẽ đồ thị hàm số sẽ giúp các em nắm được lời giải các bài tập từ SGK và học tập hiệu quả hơn.
Với việc môn Toán chuyển sang hình thức thi Trắc nghiệm sẽ khiến cho việc học và giải các bài toán Khảo sát sự biến thiên và vẽ đồ thị hàm số sẽ thay đổi khá nhiều đòi hỏi các em phải nắm vững và hiểu rõ hơn nữa các tính chất liên quan đến đồ thị của từng loại hàm số khác nhau chứ không phải chỉ chăm chăm vào phần đồ thị để lấy chắc 1 điểm như các năm trước đây.
Mục lục nội dung
1. Giải bài 1 trang 43 SGK Giải tích 12
2. Giải bài 2 trang 43 SGK Giải tích 12
3. Giải bài 3 trang 43 SGK Giải tích 12
4. Giải bài 4 trang 44 SGK Giải tích 12
5. Giải bài 5 trang 44 SGK Giải tích 12
6. Giải bài 6 trang 44 SGK Giải tích 12
7. Giải bài 7 trang 44 SGK Giải tích 12

1. Giải bài 1 trang 43 SGK Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:
a) \(\small y = 2 + 3x - x^3\)
b) \(\small y = x^3 + 4x^2 + 4x\)
c) \(\small y = x^3 + x^2+ 9x\)
d) \(\small y = -2x^3 + 5\)
Phương pháp giải
Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số bậc 3
- Tập xác định: \(D=\mathbb{R}.\)
- Sự biến thiên: Xét chiều biến thiên của hàm số
- Tính đạo hàm: \(y' = 3{\rm{a}}{{\rm{x}}^{\rm{2}}}{\rm{ + 2bx + c}}\)
- \(y' = 0 \Leftrightarrow 3{\rm{a}}{{\rm{x}}^{\rm{2}}}{\rm{ + 2bx + c = 0}}\) (Bấm máy tính nếu nghiệm chẵn, giải \(\Delta ;\Delta '\) nếu nghiệm lẻ - không được ghi nghiệm gần đúng).
- Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
- Tìm cực trị
- Tìm các giới hạn tại vô cực (\(x \to \pm \infty\))
- Hàm số bậc ba nói riêng và các hàm số đa thức nói chung không có tiệm cận đứng và tiệm cận ngang.
- Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
- Đồ thị
- Tính đối xứng: Đồ thị hàm số bậc ba nhận điểm \(I(x_0,f(x_0))\) với \(x_0\) là nghiệm phương trình \(f''(x_0)=0\) làm tâm đối xứng.
- Giao của đồ thị với trục Oy: x=0 =>y=d => (0; d)
- Giao của đồ thị với trục Ox: \(y = 0 \Leftrightarrow {\rm{a}}{{\rm{x}}^{\rm{3}}}{\rm{ + b}}{{\rm{x}}^{\rm{2}}}{\rm{ + cx + d}} = 0 \Leftrightarrow x = ?\)
- Các điểm CĐ; CT (nếu có).
- Lấy thêm một số điểm (nếu cần), điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.
Trong thực tế, khi giải bài tập để thuận lợi cho việc tính toán ta thường tính giới hạn, lập bảng biến thiên rồi mới suy ra cực trị của hàm số.
Hướng dẫn giải
Câu a: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba sau \(\small y = 2 + 3x - x^3\)
Xét hàm số y = 2 + 3x - x3
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = - \infty\)
Sự biến thiên:
Đạo hàm: y' = 3 - 3x2
Ta có: y' = 0 ⇔ x = ± 1 .
Bảng biến thiên
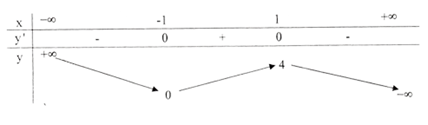
Vậy hàm số đồng biến trên các khoảng (-1;1), nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right).\)
Cực trị: Hàm số đạt cực đại tại x = 1, giá trị cực đại yCĐ = y(1) = 4, đạt cực tiểu tại x = -1 và yCT = y(-1) = 0.
Đồ thị
Ta có: y'' = -6x; y'' = 0 ⇔ x = 0. Với x = 0 ta có y = 2. Vậy đồ thị hàm số nhận điểm I(0;2) làm tâm đối xứng.
Đồ thị cắt trục Ox tại các điểm (2;0) và (-1;0), cắt Oy tại điểm (0;2).
Đồ thị hàm số nhận điểm (0;2) làm điểm uốn.
Nhận thấy, nhánh bên trái vẫn còn thiếu một điểm để vẽ đồ thị, dựa vào tính đối xứng ta chọn điểm của hoành độ x = -2 suy ra y = 4.
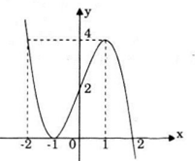
Câu b: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba sau \(\small y = x^3 + 4x^2 + 4x\)
Xét hàm số \(\small y = x^3 + 4x^2 + 4x\)
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty\).
Sự biến thiên
Đạo hàm: y' = 3x2 + 8x + 4.
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 2\\ x = - \frac{2}{3} \end{array} \right.\)
Bảng biến thiên
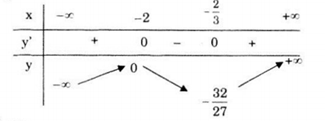
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - \frac{2}{3}; + \infty } \right)\) và nghịch biến trên \(\left( { - 2; - \frac{2}{3}} \right).\)
Cực trị
Hàm số đạt cực đại tại x=-2, giá trị cực đại ycđ = y(-2) = 0.
Hàm số đạt cực tiểu tại \(x=-\frac{2}{3}\), giá trị cực tiểu \(y_{ct}=y\left ( -\frac{2}{3} \right )=-\frac{32}{27}.\)
Đồ thị hàm số
Tâm đối xứng của đồ thị hàm số: \(y''=6x+8;\)\(y''=0\Leftrightarrow x=-\frac{4}{3}\Rightarrow y=-\frac{16}{27}.\)
Đồ thị hàm số cắt trục Oy tại điểm (0;0), cắt trục Ox tại điểm có hoành độ là nghiệm của phương trình: x3 + 4x2 + 4x = 0 ⇔ x = 0 hoặc x = -2 nên tọa độ các giao điểm là (0;0) và (-2;0).
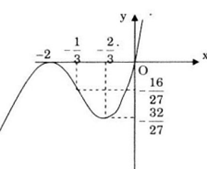
Câu c: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba sau \(\small y = x^3 + x^2+ 9x\)
Xét hàm số \(\small y = x^3 + x^2+ 9x\)
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty\).
Sự biến thiên
Đạo hàm: y' = 3x2 + 2x + 9 > 0, ∀x.
Vậy hàm số luôn đồng biến trên \(\mathbb{R}\) và không có cực trị.
Bảng biến thiên
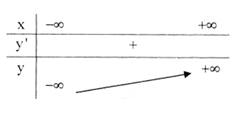
Đồ thị
Đồ thị hàm số cắt trục Ox tại điểm (0;0), cắt trục Oy tại điểm (0;0).
Đồ thị hàm số có tâm đối xứng là điểm có hoành độ là nghiệm của phương trình y'' = 0 ⇔ 6x+2 = 0 ⇔ \(x=-\frac{1}{3}.\) Suy ra tọa độ tâm đối xứng là: \(I\left ( -\frac{1}{3};-\frac{79}{27} \right ).\)
Lúc này ta vẫn chưa có đủ điểm để vẽ đồ thị hàm số, ta cần lấy thêm hai điểm có hoành độ cách đều hoành độ \(x_1\) và \(x_2\) sao cho \(\left| {{x_1} - \left( { - \frac{1}{3}} \right)} \right| = \left| {{x_2} - \left( { - \frac{1}{3}} \right)} \right|\), khi đó hai điểm này sẽ đối xứng nhau qua điểm uốn. Ta chọn các điểm (-1;-9) và \(\left ( \frac{1}{2};\frac{39}{8} \right ).\)
.png)
Câu d: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba sau \(\small y = -2x^3 + 5\)
Xét hàm số y=-2x3+5
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = - \infty\)
Sự biến thiên
Đạo hàm: y' = -6x2 ≤ 0, ∀x.
Bảng biến thiên
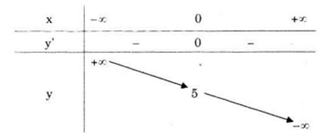
Vậy hàm số luôn nghịch biến trên R.
Hàm số không có cực trị.
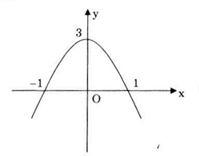
Đồ thị
Tính đối xứng: y'' = -12x; y'' = 0 ⇔ x = 0. Vậy đồ thị hàm số nhận điểm uốn I(0;5) làm tâm đối xứng.
Đồ thị hàm số cắt trục Oy tại điểm (0;5), đồ thị cắt trục Ox tại điểm \(\left( {\sqrt[3]{{\frac{5}{2}}};0} \right).\)
2. Giải bài 2 trang 43 SGK Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:
a) \(\small y = -x^4 + 8x^2 - 1\)
b) \(\small y = x^4 - 2x^2 + 2\)
c) \(\small y=\frac{1}{2}x^4+x^2-\frac{3}{2}\)
d) \(\small y = -2x^2 - x^4 + 3\)
Phương pháp giải
Trước khi giải bài 2, các em cần ôn lại bước khảo sát sự biến thiên và vẽ đồ thị hàm số bậc 4 (trùng phương):
- Tập xác định: \(D=\mathbb{R}.\)
- Sự biến thiên
+ Tính đạo hàm \(y' = 4{\rm{a}}{{\rm{x}}^{\rm{3}}}{\rm{ + 2bx}}\)
+ Ta có
\(\begin{array}{*{20}{l}}
\begin{array}{l}
y' = 0 \Leftrightarrow 4a{x^3} + 2bx = 0\\
\Leftrightarrow 2x(2a{x^2} + b) = 0
\end{array}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0}\\
{2a{x^2} + b = 0}
\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0}\\
{{x^2} = \frac{{ - b}}{{2a}}}
\end{array}} \right. \Leftrightarrow ...}
\end{array}\)
- Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
- Tìm cực trị
- Tìm các giới hạn tại vô cực (\(x \to \pm \infty\)).
- Hàm trùng phương không có Tiệm cận đứng và tiệm cận ngang.
- Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
- Đồ thị
+ Giao của đồ thị với trục Oy: x=0 =>y= c => (0;c).
+ Giao của đồ thị với trục Ox: \(y = 0 \Leftrightarrow {\rm{a}}{{\rm{x}}^{\rm{4}}}{\rm{ + b}}{{\rm{x}}^{\rm{2}}}{\rm{ + c}} = 0 \Leftrightarrow x = ? \Rightarrow (?;0)\).
+ Các điểm cực tiểu, cực đại (nếu có).
Trong thực tế, trong quá trình giải bài tập để thuận lợi hơn trong việc tính toán toán ta có thể tính giới hạn, lập bảng biến thiên trước mới đưa ra kết luận về tính đơn điệu, cực trị của hàm số
Hướng dẫn giải
Câu a: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc bốn sau \(\small y = -x^4 + 8x^2 - 1\)
Xét hàm số y=-x4+8x2-1
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = - \infty\)
Sự biến thiên:
Đạo hàm: y' =-4x3 + 16x = -4x(x2 - 4)
y' = 0 ⇔ x = 0 hoặc x = ±2 .
Bảng biến thiên
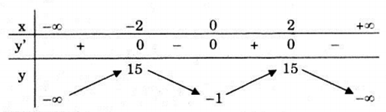
Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và (0;2), nghịch biến trên các khoảng (-2;0) và \(\left( {2; + \infty } \right).\)
Cực trị: Hàm số đạt cực đại tại x = -2 và x = 2, giá trị cực đại yCĐ = y(-2) = y(2) = 15. Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu yCT = y(0) = -1.
Đồ thị
Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Biểu thị các điểm cực trị lên hệ trục tọa độ.
Đồ thị hàm số cắt trục Ox tại các điểm
\(\left( {\sqrt {4 - \sqrt {15} } ;0} \right);\left( { - \sqrt {4 - \sqrt {15} ;0} } \right);\) \(\left( {\sqrt {4 + \sqrt {15} } ;0} \right);\left( { - \sqrt {4 + \sqrt {15} } ;0} \right)\)
đây là các điểm có tọa độ lẻ ta cần ước lượng vị trí gần đúng để vẽ đồ thị cho chính xác hơn. Đồ thị cắt trục Oy tai điểm (0;-1).
Đồ thị của hàm số
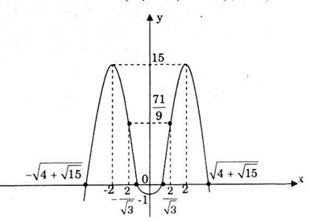
Câu b: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc bốn sau \(\small y = x^4 - 2x^2 + 2\)
Xét hàm số y = x4 - 2x2 + 2
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty\)
Sự biến thiên
Đạo hàm: y' = 4x3 - 4x = 4x(x2 - 1).
y' = 0 ⇔ x = 0 hoặc x = ±1 .
Bảng biến thiên
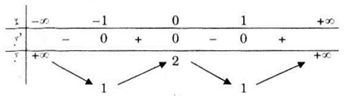
Hàm số đồng biến trên các khoảng (1;0) và \(\left( {1; + \infty } \right),\) nghịch biến trên các khoảng \(\left( { - \infty ;1} \right)\)và (0;1).
Cực trị: Hàm số đạt cực đại tại x = 0, giá trị cực đại yCĐ= y(0) = 2, hàm số đạt cực tiểu tại x = -1 và x = 1, giá trị cực tiểu yCT = y(-1) = y(1) = 1.
Đồ thị
Đồ thị hàm số nhận trục tung làm trục đối xứng.
Biểu diễn các điểm cực trị lên hệ trục tọa độ.
Đồ thị hàm số không cắt trục Ox, cắt Oy tại điểm (0;2).
Ta thây với các điểm đã có ta chưa vẽ được đồ thị hàm số, ta cần lấy thêm hai điểm một điểm có hoành độ x1 < -1 và một điểm có hoành độ x2 > 1 thuộc đồ thị hàm số và đối xứng nhau qua trục tung. Ta chọn: với x1 = -2 ta có y = 10, với x2 = 2 ta có y = 10.
Đồ thị hàm số
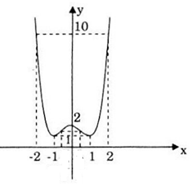
Câu c: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc bốn sau \(\small y=\frac{1}{2}x^4+x^2-\frac{3}{2}\)
Xét hàm số \(\small y=\frac{1}{2}x^4+x^2-\frac{3}{2}\)
Tập xác định:\(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty\).
Sự biến thiên
Đạo hàm: y' =2x3 + 2x = 2x(x2 + 1); y' = 0 ⇔ x = 0.
Bảng biến thiên
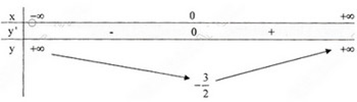
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right).\)
Cực trị: Hàm số đạt cực tiểu tại x = 0 giá trị cực tiểu \(y_{ct}=y(0)=-\frac{3}{2}.\) Hàm số không có cực đại.
Đồ thị
Đồ thị hàm số nhận trục tung làm trục đối xứng.
Đồ thị hàm số cắt trục Oy tại điểm: \(\left ( 0;-\frac{3}{2} \right )\), cắt trục Ox tại điểm có hoành độ là nghiệm của phương trình:
\(\frac{1}{4}{x^4} + {x^2} - \frac{3}{2} = 0 \Leftrightarrow x = \pm \sqrt { - 2 + \sqrt {10} } .\)
Vậy tọa độ giao điểm là:
\(\left( {\sqrt { - 2 + \sqrt {10} } ;0} \right);\left( { - \sqrt { - 2 + \sqrt {10} } ;0} \right).\)
Đồ thị
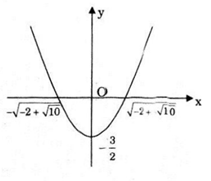
Câu d: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc bốn sau \(\small y = -2x^2 - x^4 + 3\)
Xét hàm số y = - 2x2 - x4 + 3
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = - \infty\).
Sự biến thiên
Đạo hàm: y' = -4x - 4x3 = -4x(1 + x2); y' = 0 ⇔ x = 0.
Bảng biến thiên
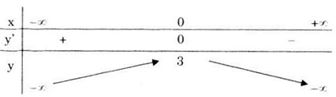
Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Cực trị: Hàm số đạt cực đại tại x = 0, giá trị cực đại yCT = y(0) = 3.
Đồ thị
Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Đồ thị hàm số cắt trục Oy tại điểm (0;3), cắt trục Ox tại các điểm có hoành độ là nghiệm của phương trình \(- {x^4} - 2{x^2} + 3 = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = - 1 \end{array} \right.\).
Đồ thị của hàm số
3. Giải bài 3 trang 43 SGK Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số phân thức sau
a) \(y=\frac{x+3}{x-1}\)
b) \(y=\frac{1-2x}{2x-4}\)
c) \(y=\frac{-x+2}{2x+1}\)
Phương pháp giải
Xét hàm số phân thức: \(y = \frac{{ax + b}}{{cx + d}}\;(c \ne 0,\;ad - bc \ne 0)\)
- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{{ - d}}{c}} \right\}.\)
- Sự biến thiên
+ Tính đạo hàm \(y' = \left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{a{\rm{d - bc}}}}{{{{{\rm{(cx + d)}}}^{\rm{2}}}}}\).
+ y’ không xác định khi \(x = \frac{{ - d}}{c}\); y’ luôn âm (hoặc dương) với mọi \(x \ne \frac{{ - d}}{c}\)
+ Hàm số đồng biến (nghịch biến) trên các khoảng \(( - \infty ; - \frac{d}{c})\) và \((-\frac{d}{c}; + \infty )\)
+ Cực trị: Hàm số không có cực trị.
- Tiệm cận
+ \(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = \frac{a}{c}\) nên đường thẳng \(y = \frac{a}{c}\) là tiệm cận ngang.
+ \(\mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ - }} \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = ( \pm )\infty\); \(\mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ + }} \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = ( \pm )\infty\) nên đường thẳng \(x = \frac{{ - d}}{c}\) là tiệm cận đứng.
- Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
- Đồ thị
+ Giao của đồ thị với trục Oy: x = 0 ⇒ y = \(\frac{b}{d}\) => (0; \(\frac{b}{d}\)).
+ Giao của đồ thị với trục Ox: \(y = 0 \Leftrightarrow \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = 0 \Rightarrow ax + b = 0 \) \(\Leftrightarrow x = \frac{{ - b}}{a} \Rightarrow (\frac{{ - b}}{a};0)\).
+ Lấy thêm một số điểm (nếu cần) - điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
+ Nhận xét về đặc trưng của đồ thị. Đồ thị nhận điểm \(I(\frac{{ - d}}{c};\frac{a}{c})\) là giao hai đường tiệm cận làm tâm đối xứng.
Hướng dẫn giải
Câu a: Khảo sát sự biến thiên và vẽ đồ thị của hàm số phân thức sau \(y=\frac{x+3}{x-1}\)
Xét hàm số \(y=\frac{x+3}{x-1}\)
Tập xác định: \(D =\mathbb{R} \backslash \left\{ 1 \right\}\).
Đạo hàm: \(\small y' = {{ - 4} \over {{{(x - 1)}^2}}} < 0,\forall x \ne 1\).
Tiệm cận
\(\small \mathop {\lim y}\limits_{x \to {1^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {1^ + }} = + \infty\) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
\(\small \mathop {\lim y}\limits_{x \to + \infty } = 1;\mathop {\lim y}\limits_{x \to - \infty } = 1\) nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
Bảng biến thiên
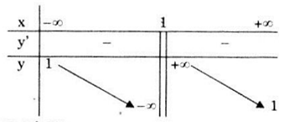
Vậy hàm số nghịch biến trên các khoảng \(\small \left( { - \infty ;1} \right)\) và \(\small \left( {1; + \infty } \right).\)
Hàm số không có cực trị.
Đồ thị hàm số
Đồ thị hàm số nhận điểm I(1;1) là giao điểm của hai đường tiệm cận làm tâm đối xứng.
Đồ thị hàm số cắt trục Ox tại điểm (-3;0), cắt Oy tại điểm (0;-3).
Nhận xét: vẫn chưa đủ điểm để vẽ đồ thị hàm số nên ta tiến hành lấy thêm 2 điểm đối xứng với (-3;0) và (0;-3) qua I(1;1) là các điểm (2;5) và (3;3).
Vậy ta có đồ thị hàm số
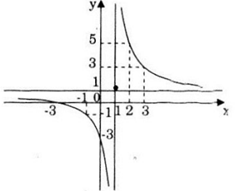
Câu b: Khảo sát sự biến thiên và vẽ đồ thị của hàm số phân thức sau \(y=\frac{1-2x}{2x-4}\)
Xét hàm số \(y=\frac{1-2x}{2x-4}\)
Tập xác định: \(D =\mathbb{R} \backslash \left\{ 2 \right\}\).
Đạo hàm: \(\small y' = {6 \over {{{\left( {2{\rm{x}} - 4} \right)}^2}}} > 0,\forall x \ne 2.\)
Tiệm cận
\(\small \mathop {\lim y}\limits_{x \to {2^ - }} = + \infty ;\mathop {\lim y}\limits_{x \to {2^ + }} = - \infty\) nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
\(\small \mathop {\lim y}\limits_{x \to + \infty } = -1;\mathop {\lim y}\limits_{x \to - \infty } = -1\) nên đường thẳng y =- 1 là tiệm cận ngang của đồ thị hàm số.
Bảng biến thiên
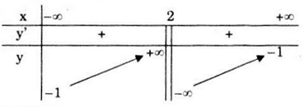
Hàm số đồng biến trên khoảng \(\small \left( { - \infty ;2} \right)\) và \(\small \left( {2; + \infty } \right)\).
Hàm số không có cực trị.
Đồ thị hàm số
Đồ thị hàm số nhận điểm I(2;-1) làm tâm đối xứng.
Đồ thị hàm số cắt trục Ox tại \(\small \left ( \frac{1}{2};0 \right );\) cắt trục Oy tại \(\small \left (0;-\frac{1}{4} \right );\)
Ta lấy thêm một điểm thuộc nhánh còn lại để vẽ đồ thị hàm số: với x=3 suy ra \(\small y=\frac{5}{2}.\)
Đồ thị hàm số
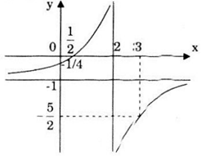
Câu c: Khảo sát sự biến thiên và vẽ đồ thị của hàm số phân thức sau \(y=\frac{-x+2}{2x+1}\)
Xét hàm số \(y=\frac{-x+2}{2x+1}\)
Tập xác định: \(D =\mathbb{R} \backslash \left\{ -\frac{1}{2} \right\}\).
Đạo hàm: \(\small y' = {{ - 5} \over {{{\left( {2{\rm{x}} + 1} \right)}^2}}} < 0,\forall x \ne - {1 \over 2}\).
Tiệm cận
\(\mathop {\lim y}\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ - }} = + \infty\) nên đường thẳng \(x=-\frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số.
\(\small \mathop {\lim y}\limits_{x \to + \infty } = - \frac{1}{2};\mathop {\lim y}\limits_{x \to - \infty } = - \frac{1}{2}\) nên đường thẳng \(y=-\frac{1}{2}\) là tiệm cận ngang của đồ thị hàm số.
Bảng biến thiên
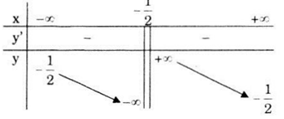
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right).\)
Hàm số không có cực trị
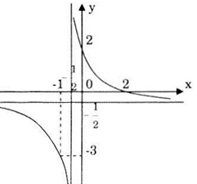
Đồ thị
Đồ thị hàm số nhận điểm \(I\left( { - \frac{1}{2}; -\frac{1}{2}} \right)\) làm tâm đối xứng.
Đồ thị hàm số cắt trục Ox tại điểm (2;0), cắt trục Oy tại điểm (0;). Ta lấy điểm (-1;-3) thuộc nhánh còn lại để thuận lợi hơn cho việc vễ đồ thị.
4. Giải bài 4 trang 44 SGK Giải tích 12
Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau
a) \(\small x^3 - 3x^2 + 5 = 0\)
b) \(\small -2x^3 + 3x^2 - 2 = 0\)
c) \(\small 2x^2 - x^4 = -1\)
Phương pháp giải
hực chất yêu cầu bài tập 3 là khảo sát sự biến thiên và vẽ đồ thị hàm số. Sau đó từ đồ thị hàm số suy ra số nghiệm của phương trình cần tìm.
Số nghiệm của các phương trình đã cho chính là số giao điểm của đồ thị hàm số y = f(x) ở vế trái của phương trình cới trục hoành ở câu a, b và với đường thẳng y = -1 ở câu c.
Hướng dẫn giải
Câu a: Bằng cách khảo sát hàm số, hãy tìm số nghiệm của phương trình sau \(\small x^3 - 3x^2 + 5 = 0\)
Xét hàm số \(y=x^3 - 3x^2 + 5\)
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty .\)
Sự biến thiên
Đạo hàm: y' = 3x2 - 6x = 3x(x - 2); y' = 0 ⇔ x = 0, x = 2.
Bảng biến thiên
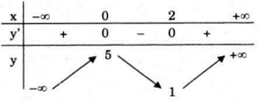
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng (0;2).
Cực trị: Hàm số đạt cực đại tại x = 0, giá trị cực đại yCĐ = y(0) = 5; đạt cực tiểu tại x = 2, giá trị cực tiểu yCT = y(2) = 1.
Đồ thị
Tính đối xứng: y'' = 6x - 6; y'' = 0 ⇔ x = 1. Vậy đồ thị hàm số nhận điểm (1;3) làm tâm đối xứng.
Đồ thị hàm số cắt trục Oy tại điểm (0;5).
Đồ thị hàm số đi qua các điểm (-1;1); (3;5).
Đồ thị của hàm số
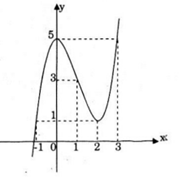
Từ đồ thị ta thấy phương trình \(\small x^3 - 3x^2 + 5 = 0\) có duy nhất một nghiệm.
Câu b: Bằng cách khảo sát hàm số, hãy tìm số nghiệm của phương trình sau \(\small -2x^3 + 3x^2 - 2 = 0\)
Xét hàm số y = -2x3 + 3x2 - 2
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty .\)
Sự biến thiên
Đạo hàm: y' = -6x2 + 6x = -6x(x - 1); y' = 0 ⇔ x = 0,x = 1.
Bảng biến thiên
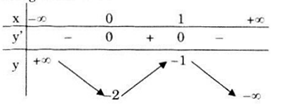
Hàm số đồng biến trên khoảng (0;1); nghịch biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {1; + \infty } \right).\)
Cực trị: Hàm số đạt cực đại tại x = 1, giá trị cực đại yCĐ = y(1) = -1, hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu yCT = y(0) = -2.
Đồ thị hàm số
Tính đối xứng
\(y''=-12x+6;y''=0\Leftrightarrow x=\frac{1}{2}.\)
Nên tọa độ tâm đối xứng là \(I\left ( \frac{1}{2};-\frac{3}{2} \right ).\)
Đồ thị hàm số đi qua các điểm: (-1;3); (2;-6).
Đồ thị của hàm số
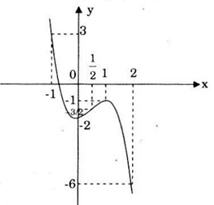
Từ đồ thị hàm số ta thấy phương trình \(\small -2x^3 + 3x^2 - 2 = 0\) có nghiệm duy nhất.
Câu c: Bằng cách khảo sát hàm số, hãy tìm số nghiệm của phương trình sau \(\small 2x^2 - x^4 = -1\)
Xét hàm số y = \(\small 2x^2 - x^4 = -1\)
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty .\)
Sự biến thiên
Đạo hàm: y' = 4x - 4x3 = 4x(1 - x2); y' = 0 ⇔ x = 0,x = ±1.
Bảng biến thiên
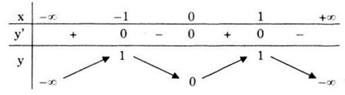
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và (0;1); nghịch biến trên các khoảng (-1;0) và \(\left( {1; + \infty } \right).\)
Cực trị: Hàm số đạt cực đại tại x = -1 và x = 1, giá trị cực đại yCĐ = y(-1) = y(1) = 1; đạt cực tiểu tại x = 0, giá trị cực tiểu yCT = y(0) = 0.
Đồ thị
Tính đối xứng: Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Đồ thị hàm số cắt trục Ox tại điểm (0;0); \(\left( {-\sqrt 2;0 } \right)\) và \(\left( {\sqrt 2;0 } \right)\); cắt truc Oy tại điểm (0;0).
Đồ thị của hàm số
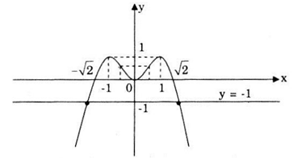
Đồ thị hàm số f(x) và đường thẳng y = - 1 như hình bên.
Từ đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt.
5. Giải bài 5 trang 44 SGK Giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số \(\small y = -x^3 + 3x + 1\)
b) Dựa vào đồ thị (C), biện luận về số nghiệm của phương trình sau theo tham số m.
\(\small x^3 - 3x + m = 0.\)
Phương pháp giải
Câu a là một bài khảo sát sự biến thiên và vẽ đồ thị hàm tương tự câu 1 đã làm nên không nhắc lại ở đây, trọng tâm bài toán này là ở câu b.
Đây là bài toán
Cho hàm số y = f(x) có đồ thị (C). Dựa vào đồ thị (C) biện luận số nghiệm của phương trình g(x;m) = 0 với m là tham số.
Với bài 5, ta sẽ chuyển bài toán về dạng:
f(x) = h(m), trong đó h(m) là một hàm phụ thuộc vào tham số m.
- Vẽ đồ thị hàm số y = f(x).
- Đường thẳng y = h(m) di động song song với trục hoành, dựa vào số giao diểm của đường thẳng y = h(m) với đồ thị hàm số y = f(x) để suy ra số nghiệm của phương trình g(x;m) = 0.
Đó là phương pháp để giải bài toán này, có thể nhiều em khi đọc qua phần lý thuyết này vẫn chưa hình dung được phải làm như thế nào. Vậy xin mời các em tham khảo lời giải chi tiết sau để hiểu và nắm phương pháp làm bài.
Hướng dẫn giải
Câu a: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số \(\small y = -x^3 + 3x + 1\)
Với m = 1 ta có hàm số: y = -x3 + 3x + 1
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty .\)
Sự biến thiên
Đạo hàm: y' = -3x2 + 3 = -3(x2 - 1); y' = 0 ⇔ x = -1, x = 1.
Bảng biến thiên
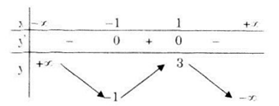
Hàm số đồng biến trên khoảng (-1;1), nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right).\)
Cực trị: Hàm số đạt cực đại tại x=1, giá trị cực tiểu yCĐ = y(1) = 3; đạt cực tiểu tại x = - 1, giá trị cực tiểu yCT = y(-1) = -1.
Đồ thị
Tính đối xứng: y'' = - 6x, y'' = 0 ⇔ x = 0. Vậy tọa độ tâm đối xứng của đồ thị hàm số là (0;1).
Đồ thị hàm số đi qua các điểm (-2;3); (2;-1).
Đồ thị hàm số
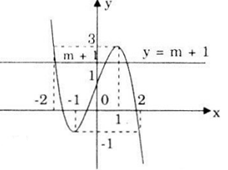
Câu b: Dựa vào đồ thị (C), biện luận về số nghiệm của phương trình sau theo tham số m.
\(\small x^3 - 3x + m = 0.\)
Xét phương trình x3 - 3x + m = 0 ⇔ - x3 + 3x + 1 = m + 1 (1).
Số nghiệm của (1) chính là số giao điểm của đồ thị (C) với đường thẳng (d): y = m + 1.
Từ đồ thị ta thấy
- Khi: m + 1 < -1 ⇔ m < -2: (d) cắt (C) tại 1 điểm suy ra (1) có 1 nghiệm.
- Khi: m + 1 = -1 ⇔ m = -2: (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm suy ra (1) có 2 nghiệm.
- Khi: -1 < m + 1 < 3 ⇔ -2 < m < 2: (d) cắt (C) tại 3 điểm suy ra (1) có 3 nghiệm.
- Khi: m + 1 = 3 ⇔ m = 2: (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm suy ra (1) có 2 nghiệm.
- Khi: m + 1 > 3 ⇔ m > 2: (d) cắt (C) tại 1 điểm suy ra (1) có 1 nghiệm.
6. Giải bài 6 trang 44 SGK Giải tích 12
Cho hàm số \(y=\frac{mx-1}{2x+m}\).
a) Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Xác định m để tiệm cận đứng đồ thị đi qua \(A(-1 ; \sqrt{2}).\)
c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 2.
Phương pháp giải
Để giải câu a bài 6, các em cần nắm được điều kiện để hàm số đồng biến trên một miền cho trước
Hàm số \(y=f(x)\) đồng biến trên miền D khi một trong hai điều kiện sau được thỏa mãn:
- \(f'(x) > 0,\forall x \in D\).
- \(f'(x) \geq 0,\forall x \in D\) và \(f'(x) = 0\) chỉ tại một số điểm hữu hạn \(x_0 \in D\) (Phương trình \(f'(x) = 0\) có hữu hạn nghiệm).
Với câu b bài 6, ta tìm tiệm cận đứng của đồ thị hàm số theo m, rồi từ dữ kiện đường tiệm cận đó đi qua một điểm ta tìm được giá trị m.
Chú ý: khi chỉ xét tiệm cận đứng ta chỉ cần quan tâm đến hoành độ điểm mà tiệm cận đi qua.
Hướng dẫn giải
Câu a: Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên mỗi khoảng xác định của nó
Xét hàm số \(y=\frac{mx-1}{2x+m}\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{m}{2}} \right\}\)
\(y' = \frac{{{m^2} + 2}}{{\left( {2x + m} \right)}} > 0,\forall m\) và \(\forall x \in \mathbb{R}\backslash \left\{ { - \frac{m}{2}} \right\}.\)
Vậy hàm số luôn đồng biến trên các khoảng \(\left( { - \infty ; - \frac{m}{2}} \right)\) và \(\left( { - \frac{m}{2}; + \infty } \right).\)
Câu b: Xác định m để tiệm cận đứng đồ thị đi qua \(A(-1 ; \sqrt{2}).\)
Điều kiện đề hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có tiệm cận đứng là:
\(\left\{ \begin{array}{l} c \ne 0\\ ad - bc \ne 0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} c = 2 \ne 0\\ {m^2} + 2 \ne 0,\forall m \end{array} \right.\)
(luôn đúng).
Ta có: \(\mathop {\lim y}\limits_{x \to {{\left( { - \frac{m}{2}} \right)}^ + }} = \mathop {\lim y}\limits_{x \to {{\left( { - \frac{m}{2}} \right)}^ + }} \frac{{mx - 1}}{{2x + m}} = - \infty ;\) \(\mathop {\lim y}\limits_{x \to {{\left( { - \frac{m}{2}} \right)}^ - }} = \mathop {\lim y}\limits_{x \to {{\left( { - \frac{m}{2}} \right)}^ - }} \frac{{mx - 1}}{{2x + m}} = + \infty\)
Nên đường thẳng \(x=-\frac{m}{2}\) là tiệm cận đứng của đồ thị hàm số.
Tiệm cận đứng đi qua \(A\left( { - 1;\sqrt 2 } \right)\) khi và chỉ khi: \(- \frac{m}{2} = - 1 \Leftrightarrow m = 2.\)
Khi tìm điều kiện liên quan đến tiệm cận đứng ta chỉ cần quan tâm đến hoành độ, cụ thể trong bài 6, đường thẳng x = -1 sẽ đi qua \(A\left( { - 1;\sqrt 2 } \right)\).
Câu c: Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 2.
Với m = 2, ta có hàm số \(y = \frac{{2x - 1}}{{2x + 2}}\)
Tập xác định \(D = \backslash \left\{ { - 1} \right\}.\)
Tiệm cận
\(\mathop {\lim y}\limits_{x \to {{\left( { - 1} \right)}^ - }} = \mathop {\lim y}\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{2x - 1}}{{2x + 2}} = + \infty ;\) \(\mathop {\lim y}\limits_{x \to {{\left( { - 1} \right)}^ + }} = \mathop {\lim y}\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{2x - 1}}{{2x + 2}} = - \infty\)
Nên đồ thị hàm số nhận đường thẳng x = -1 làm tiệm cận đứng.
\(\mathop {\lim y}\limits_{x \to - \infty } = \mathop {\lim y}\limits_{x \to - \infty } \frac{{2x - 1}}{{2x + 2}} = 1;\) \(\mathop {\lim y}\limits_{x \to + \infty } = \mathop {\lim y}\limits_{x \to + \infty } \frac{{2x - 1}}{{2x + 2}} = 1\)
Nên đồ thị hàm số nhận đường thẳng y=1 làm tiệm cận ngang.
Đạo hàm: \(y' = \frac{6}{{{{(2x + 2)}^2}}} > 0,\forall x \ne - 1.\)
Bảng biến thiên
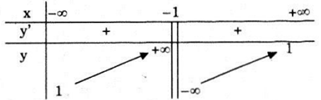
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right).\)
Hàm số không có cực trị.
Đồ thị
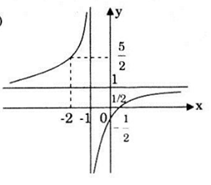
Đồ thị hàm số nhận điểm I(-1;1) làm tâm đối xứng.
Đồ thị hàm số cắt trục Ox tại \(\left ( \frac{1}{2};0 \right )\); cắt Oy tại \(\left ( 0;-\frac{1}{2} \right )\).
Đồ thị hàm số đi qua điểm \(\left ( -2;\frac{5}{2} \right )\).
Đồ thị của hàm số
7. Giải bài 7 trang 44 SGK Giải tích 12
Cho hàm số \(y=\frac{1}{4}x^4+\frac{1}{2}x^2+m\).
a) Với giá trị nào của tham số m, đồ thị của hàm số đi qua điểm (-1;1)?
b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
c) Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng \(\frac{7}{4}\).
Phương pháp giải
- Câu a, yêu cầu tìm tham số m để đồ thị hàm số đi qua một điểm cho trước, rất đơn giản ta chỉ cần thay tọa điểm đó vào hàm số tương ứng y là tung độ, x là hoành độ, khi đó ta chỉ cần giải phương trình tìm tham số m.
- Câu b, tham giá trị của m vào hàm số ta sẽ được một hàm số cụ thể sau đó thực hiện các bước khảo sát sự biến thiên và vẽ đồ thị hàm số này.
- Câu c, phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại tiếp điểm M(x0,y0) thuộc đồ thị hàm số đã học ở chương trình lớp 11 có dạng \(y-y_0=f'(x_0)(x-x_0)\)
Như vậy trong câu c, ta cần phải xác định được tọa độ tiếp điểm. Mặc khác theo đề bài ta có tung độ tiếp điểm bằng \(\frac{7}{4}\), từ đó ta thay vào hàm số sẽ được tìm hoành độ.
Hướng dẫn giải
Câu a: Với giá trị nào của tham số m, đồ thị của hàm số đi qua điểm (-1;1)?
Điểm (-1;1) thuộc đồ thị của hàm số nên ta có:
\(1 = \frac{1}{4}{\left( { - 1} \right)^4} + \frac{1}{2}{\left( { - 1} \right)^2} + m \Leftrightarrow m = \frac{1}{4}\).
Câu b: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
Với m = 1 ta có hàm số
\(y=\frac{1}{4}x^{4}+\frac{1}{2}x^{2}+1\)
Tập xác định: \(D=\mathbb{R}.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty\)
Sự biến thiên
\(y = {x^3} + x = x\left( {{x^2} + 1} \right);y' = 0 \Leftrightarrow x = 0\)
Bảng biến thiên
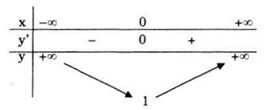
Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right).\)
Cực trị: Hàm số đạt cực tiểu tại x = 0 và giá trị cực tiểu yCT = y(0) = 1.
Đồ thị
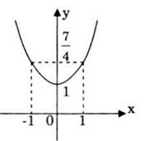
Đồ thị hàm số cắt trục Oy tại điểm (0;1).
Với x = 1 ta có \(y=\frac{7}{4}.\)
Với x = -1 ta có \(y=\frac{7}{4}.\)
Đồ thị hàm số
Câu c: Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng \(\frac{7}{4}\).
Với \(y=\frac{7}{4}\) ta có
\(\begin{array}{l}
\frac{1}{4}{x^4} + \frac{1}{2}{x^2} + 1 = \frac{7}{4} \Leftrightarrow {x^4} + 2{x^2} - 3 = 0\\
\Leftrightarrow {x^2} = 1 \Leftrightarrow x = \pm 1
\end{array}\)
Vậy hai điểm thuộc (C) có tung độ \(y=\frac{7}{4}\) là \(A\left ( 1;\frac{7}{4} \right )\)và \(B\left ( -1;\frac{7}{4} \right )\).
Ta có: y' = x3 + x suy ra: y'(-1) = - 2, y'(1) = 2.
Phương trình tiếp tuyến với (C) tại A là: \(y - \frac{7}{4} = y'(1)(x - 1) \Leftrightarrow y = 2x - \frac{1}{4}.\)
Phương trình tiếp tuyến với (C) tại B là: \(y - \frac{7}{4} = y'(-1)(x + 1) \Leftrightarrow y = -2x - \frac{1}{4}.\)
8. Giải bài 8 trang 44 SGK Giải tích 12
Cho hàm số \(y=x^3+(m+3)x^2+1-m\) (m là tham số) có đồ thị là (Cm)
a) Xác định m để hàm số có điểm cực đại là x = -1
b) Xác định m để đồ thị (Cm) cắt trục hoành tại x = -2
Phương pháp giải
- Sử dụng kiến thức: hàm số \(y = f\left( x \right)\) đạt cực đại tại tại điểm \(x= {x_0} \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right..\)
- Đồ thị hàm số cắt trục hoành tại điểm có M hoành độ \(x = a \Rightarrow M(a;0) \). Thay tọa độ điểm M vào công thức hàm số để tìm m.
Hướng dẫn giải
Câu a: Xác định m để hàm số có điểm cực đại là x = -1
\(y = {x^3} + \left( {m + 3} \right){x^2} + 1 - m.\)
Ta có: \(y' = 3{x^2} + 2\left( {m + 3} \right)x \Rightarrow y'' = 6x + 2\left( {m + 3} \right).\)
Hàm số đạt cực đại tại điểm \(x = - 1\) \(\Rightarrow \left\{ \begin{array}{l}y'\left( -1 \right) = 0\\y''\left( -1 \right) < 0\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}3 - 2\left( {m + 3} \right) = 0\\ - 6 + 2\left( {m + 3} \right) < 0\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}m = - \dfrac{3}{2}\\m < 0\end{array} \right. \Rightarrow m = - \dfrac{3}{2}.\)
Vậy \(m=-\dfrac{3}{2}.\) thì hàm số đã cho đạt cực đại tại \(x=-1\).
Câu b: Xác định m để đồ thị (Cm) cắt trục hoành tại x = -2
Đồ thị hàm số cắt trục hoành tại điểm có M hoành độ \(x = -2 \Rightarrow M(-2;0) \).
\(\begin{array}{l}\Rightarrow {\left( { - 2} \right)^3} + \left( {m + 3} \right){\left( { - 2} \right)^2} + 1 - m = 0\\ \Leftrightarrow - 8 + 4\left( {m + 3} \right) + 1 - m = 0\\\Leftrightarrow 4m + 5 - m = 0\\\Leftrightarrow 3m = - 5\\\Leftrightarrow m = - \dfrac{5}{3}.\end{array}\)
9. Giải bài 9 trang 44 SGK Giải tích 12
Cho hàm số \(y = \frac{{\left( {m + 1} \right)x - 2m + 1}}{{x - 1}}\) (m là tham số) có đồ thị là (G).
a) Xác định m để đồ thị (G) đi qua điểm (0 ; -1)
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m tìm được
c) Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung
Phương pháp giải
- Thay tọa độ điểm đề bài đã cho vào công thức hàm số để tìm m.
- Thay giá trị m đã tìm được ở câu a vào đồ thị hàm số sau đó khảo sát và vẽ đồ thị hàm số.
- Đồ thị hàm số cắt trục tung tại điểm có M tung độ \(y = y_0 \Rightarrow M(0;y_0) \).
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại \(M\left( {{x_0};{y_0}} \right)\) bằng công thức: \(y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\).
Hướng dẫn giải
Câu a: Xác định m để đồ thị (G) đi qua điểm (0 ; -1)
Theo đề bài ta có \((0 ; -1) ∈ (G) \) \(⇔ -1=\dfrac{(m+1)\cdot 0-2m+1}{0-1}\) \( \Leftrightarrow - 1 = 2m - 1 \Leftrightarrow 2m = 0\) \(\Leftrightarrow m=0.\)
Câu b: Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m tìm được
Với \(m = 0\) ta được hàm số \(y=\dfrac{x+1}{x-1}\) (G0).
Tập xác định: \(D=\mathbb R \backslash {\rm{\{ }}1\}\)
- Sự biến thiên
Ta có: \(y' = {{ - 2} \over {{{(x - 1)}^2}}} < 0\forall x \in D\)
+ Hàm số nghịch biến trên khoảng: \((-\infty;1)\) và \((1;+\infty)\).
+ Cực trịHàm số không có cực trị.
+ Tiệm cận
\(\eqalign{
& \mathop {\lim y}\limits_{x \to \pm \infty } = 1 \cr
& \mathop {\lim y}\limits_{x \to {1^ - }} = - \infty \cr
& \mathop {\lim y}\limits_{x \to {1^ + }} = + \infty \cr} \)
Tiệm cận đứng là: \(x=1\), tiệm cận ngang là: \(y=1\)
- Bảng biến thiên:
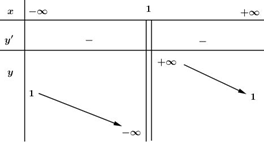
- Đồ thị
Đồ thị hàm số giao trục \(Ox\) tại \((-1;0)\), trục \(Oy\) tại \((0;-1)\)
Đồ thị hàm số nhận \(I(1;1)\) làm tâm đối xứng.
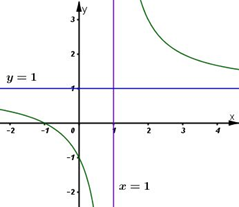
Câu c: Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung
G0) cắt trục tung tại \(M(0 ; -1)\).
\(y'=\dfrac{-2}{(x-1)^{2}}\Rightarrow y'(0) = -2\).
Phương trình tiếp tuyến của (G0) tại \(M\) là: \(y - (-1) = y'(0)(x - 0) \) \(⇔ y= -2x - 1\)
Tham khảo thêm
- docx Giải bài tập SGK Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
- docx Giải bài tập SGK Toán 12 Bài 2: Cực trị của hàm số
- docx Giải bài tập SGK Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- docx Giải bài tập SGK Toán 12 Bài 4: Đường tiệm cận
- docx Giải bài tập SGK Toán 12 Ôn tập Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ ĐTHS



.png)
