Giải bài tập SGK Toán 12 Ôn tập chương 2: Hàm số lũy thừa, Hàm số mũ và Hàm số Lôgarit

Hãy nên các tính chất của luỹ thừa với số mũ thực.​

Hướng dẫn giải

Các tính chất quan trọng của lũy thừa với số mũ thực:

Với số thực \(a>0\) ta có các tính chất sau

• \(a^x.a^y=a^{x+y} \ \ \ x, y\in \mathbb{R}\)
• \(\frac{a^x}{a^y}=a^{x-y} \ \ \ x, y \in \mathbb{R}\)
• \((a^x)^y=a^{xy} \ \ \ x,y\in \mathbb{R}\)
• \(\sqrt[x]{a^y}=a^{\frac{y}{x}} \ \ \ x\in N, x\geq 2, y\in \mathbb{R}\)
• \((a.b)^x=a^x.b^x\)
• \(\left ( \frac{a}{b} \right )^y=\frac{a^y}{b^y}\)

Hãy nên các tính chất của hàm số luỹ thừa

Hướng dẫn giải

Tính chất của hàm số luỹ thừa \(y=x^\alpha\)

Tập xác định của hàm số lũy thừa luôn chứa khoảng \(\left( {0; + \infty } \right)\) với mọi \(\alpha \in \mathbb{R}\). 

Trong trường hợp tổng quát ta khảo sát hàm số \(y=x^{\alpha}\) trên khoảng \(\left( {0; + \infty } \right)\)​, ta được bảng tóm tắt sau

Hình dạng của đồ thị hàm số lũy thừa trong các trường hợp xét trên tập \(\left( {0; + \infty } \right)\):

♦ Chú ý

Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.

Hãy nêu các tính chất của hàm số mũ và hàm số logarit.

Hướng dẫn giải

Tính chất hàm số mũ

• Tập xác định: \(\mathbb{R}.\)
• Tập giá trị: \((0;+\infty )\)
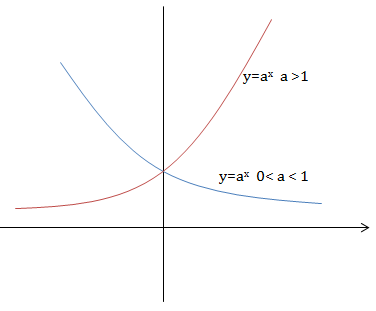
• Với \(a>1\) hàm số \(y=a^x\) đồng biến trên \(\mathbb{R}.\)
• Với \(0
• Đồ thị hàm số mũ nhận trục \(Ox\) làm tiệm cận ngang.

Tính chất hàm số Lôgarit

• Tập xác định: \(\left( {0; + \infty } \right).\)
• Tập giá trị: \(\mathbb{R}.\)
• Với \(a>1\): \(y=\log_ax\) là hàm số đồng biến trên \(\left( {0; + \infty } \right).\)
• Với \(0
• Với \(x_1>0,x_2>0\): \(\log_ax_1=\log_ax_2\Leftrightarrow x_1=x_2\)

Tìm tập xác định của các hàm số

a) \(y=\frac{1}{3^x-3}.\)

b) \(y=log\frac{x-1}{2x-3}.\)

c) \(y=log\sqrt{x^2-x-12}.\)

d) \(y=\sqrt{25^x-5^x}\).

Phương pháp giải

Áp dụng các tính chất của hàm số lũy thừa và hàm số mũ

\(\displaystyle \frac{A}{B}\) xác định khi và chỉ khi \(\displaystyle B \ne 0\).

\(\displaystyle \sqrt A \) xác định khi và chỉ khi \(\displaystyle A \ge 0\)

\(\displaystyle {\log _a}x\) xác định khi và chỉ khi \(\displaystyle x>0\)

\(\displaystyle \frac{1}{{\sqrt A }}\) xác định khi và chỉ khi \(\displaystyle A>0\).

Hướng dẫn giải

Câu a

\(y=\frac{1}{3^x-3}\)

Để hàm số có nghĩa thì \(3^x\neq 3\Leftrightarrow x\neq 1\)

⇒ Tập xác định của hàm số là: D = R\ {1}.

Câu b

\(y=log\frac{x-1}{2x-3}\)

Để hàm số có nghĩa thì: \(\frac{x-1}{2x-3}>0\Leftrightarrow \bigg \lbrack \begin{matrix} x> \frac{3}{2}\\ x< 1 \end{matrix}\)

⇒ Tập xác định của hàm số là: \(D=(-\infty ;1)\cup (\frac{3}{2};+\infty )\).

Câu c

\(y=log\sqrt{x^2-x-12}\)

Để hàm số có nghĩa thì \(x^2-x-12>0\Leftrightarrow \bigg \lbrack \begin{matrix} x<-3\\ x>4 \end{matrix}\)

⇒ Tập xác định của hàm số là: \(D=(-\infty ;-3)\cup (4;+\infty )\).

Câu d

\(y=\sqrt{25^x-5^x}\)

Để hàm số có nghĩa thì \(25^x-5^x\geq 0\Leftrightarrow 5^{2x}\geq 5^x\Leftrightarrow x\geq 0\)

⇒ Tập xác định của hàm số là: \(D=[0; +\infty )\)

Biết \({4^x} + {\rm{ }}{4^{ - x}} = {\rm{ }}23\). Hãy tính: \({2^x} + {\rm{ }}{2^{ - x}}\)

Phương pháp giải

Sử dụng khai triển hằng đẳng thức \({\left( {{2^x} + {2^{ - x}}} \right)^2}\)

Hướng dẫn giải

Ta có

\(\begin{array}{l}{\left( {{2^x} + {2^{ - x}}} \right)^2} \\= {\left( {{2^x}} \right)^2} + {2.2^x}{.2^{ - x}} + {\left( {{2^{ - x}}} \right)^2}\\= {4^x} + {4^{ - x}} + 2 = 23 + 2 = 25\\ \Rightarrow {\left( {{2^x} + {2^{ - x}}} \right)^2} = 25\\ \Rightarrow \left| {{2^x} + {2^{ - x}}} \right| = 5\end{array}\)

Mà \({2^x} > 0;{2^{ - x}} > 0,\forall x\) nên \({2^x} + {2^{ - x}} > 0\)

\(⇒ {{2^x} + {\rm{ }}{2^{ - x}} = {\rm{ }}5}\).

Cho \(log_ab=3, log_ac=-2\). Tính \(log_ax\) với

a) \(x=a^3b^2\sqrt{c}\)

b) \(x=\frac{a^4\sqrt[3]{b}}{c^3}\)

Phương pháp giải

Sử dụng công thức cộng trừ các logarrit cùng cơ số:

\(\begin{array}{l}
{\log _a}x + {\log _a}y = {\log _a}\left( {xy} \right)\\
{\log _a}x - {\log _a}y = {\log _a}\frac{x}{y}\\
{\log _{{a^n}}}{x^m} = \frac{m}{n}{\log _a}x
\end{array}\)

Hướng dẫn giải

Câu a

\(\begin{array}{l}\,{\log _a}x = {\log _a}\left( {{a^3}{b^2}\sqrt c } \right)\\= {\log _a}{a^3} + {\log _a}{b^2} + {\log _a}\sqrt c \\= {\log _a}{a^3} + {\log _a}{b^2} + {\log _a}{c^{\frac{1}{2}}}\\= 3{\log _a}a + 2{\log _a}b + \dfrac{1}{2}{\log _a}c\\= 3 + 2.3 + \dfrac{1}{2}\left( { - 2} \right) = 8\end{array}\)

Câu b

\(\begin{array}{l}\,{\log _a}x = {\log _a}\dfrac{{{a^4}\sqrt[3]{b}}}{{{c^3}}}\\= {\log _a}{a^4} + {\log _a}\sqrt[3]{b} - {\log _a}{c^3}\\= {\log _a}{a^4} + {\log _a}{b^{\frac{1}{3}}} - {\log _a}{c^3}\\= 4{\log _a}a + \dfrac{1}{3}{\log _a}b - 3{\log _a}c\\= 4.1 + \dfrac{1}{3}.3 - 3\left( { - 2} \right)\\= 11\end{array}\)

Giải các phương trình

a) \({{3}^{x+4}}+{{3.5}^{x+3}}={{5}^{x+4}}+{{3}^{x+3}};\) 

b) \({{25}^{x}}-{{6.5}^{x}}+5=0;\)

c) \({{4.9}^{x}}+{{12}^{x}}-{{3.16}^{x}}=0;\) 

d) \({{\log }_{7}}\left( x-1 \right){{\log }_{7}}x={{\log }_{7}}x;\)

e) \({{\log }_{3}}x+{{\log }_{\sqrt{3}}}x+{{\log }_{\frac{1}{3}}}x=6;\)

f) \(\log \dfrac{x+8}{x-1}=\log x.\)

Phương pháp giải

Vận dụng các phương pháp giải phương trình mũ và lôgarit đã học ở bài 5 chương 2 Giải tích 12

Hướng dẫn giải

Câu a

\({3^{x + 4}} + {3.5^{x + 3}} = {5^{x + 4}} + {3^{x + 3}}\) \( \Leftrightarrow {3^{\left( {x + 3} \right) + 1}} + {3.5^{x + 3}} - {5^{x + 4}} - {3^{x + 3}} = 0\) \( \Leftrightarrow \left( {{{3.3}^{x + 3}} - {3^{x + 3}}} \right) + \left( {{{3.5}^{x + 3}} - {5^{x + 4}}} \right) = 0\) \( \Leftrightarrow {3^{x + 3}}\left( {3 - 1} \right) + {5^{x + 3}}\left( {3 - 5} \right) = 0\) \( \Leftrightarrow {2.3^{x + 3}} - {2.5^{x + 3}} = 0\) \( \Leftrightarrow {2.3^{x + 3}} = {2.5^{x + 3}}\) \( \Leftrightarrow {3^{x + 3}} = {5^{x + 3}}\) \( \Leftrightarrow \dfrac{{{3^{x + 3}}}}{{{5^{x + 3}}}} = 1\) \(\Leftrightarrow {\left( {\dfrac{3}{5}} \right)^{x + 3}} = 1={\left( {\dfrac{3}{5}} \right)^{0}}\) \(\Leftrightarrow x + 3 = 0 \Leftrightarrow x = - 3\)

Vậy tập nghiệm của phương trình là \(S = \left\{ { - 3} \right\}\).

Câu b

\({25^x}-{\rm{ }}{6.5^x} + {\rm{ }}5{\rm{ }} = {\rm{ }}0\) \(\Leftrightarrow {(5^{x})^2}-{6.5^x} + 5= 0\)

Đặt \(t = 5^x\) (\(t > 0\)).

Phương trình trở thành:

\({t^2} - 6t + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = 5\end{array} \right. \) \(\Leftrightarrow\left[ \begin{array}{l}{5^x} = 1\\{5^x} = 5\end{array} \right. \Leftrightarrow \left[\begin{array}{l}x = 0\\x = 1\end{array} \right.\)

Vậy tập nghiệm của phương trình là \(S = \left\{ {0;1} \right\}\).

Câu c

\({4.9^x} + {\rm{ }}{12^x}-{\rm{ }}{3.16^x} = {\rm{ }}0\)

Chia cả hai vế của phương trình cho \(16^x>0\) ta được:

\( \Leftrightarrow 4.\dfrac{{{9^x}}}{{{{16}^x}}} + \dfrac{{{{12}^x}}}{{{{16}^x}}} - 3 = 0\)

\( \Leftrightarrow 4.{\left( {\dfrac{9}{{16}}} \right)^x} + {\left( {\dfrac{{12}}{{16}}} \right)^x} - 3 = 0 \)

\(\Leftrightarrow 4.{\left( {\dfrac{3}{4}} \right)^{2x}} + {\left( {\dfrac{3}{4}} \right)^x} - 3 = 0\)

Đặt \(t = {\left( {\dfrac{3}{4}} \right)^x} (t > 0) \) ta được phương trình:

\(4{t^2} + t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{3}{4}\,\,\left( {tm} \right)\\t = - 1\,\left( {ktm} \right)\end{array} \right. \) \( \Rightarrow {\left( {\dfrac{3}{4}} \right)^x} = \dfrac{3}{4} = {\left( {\dfrac{3}{4}} \right)^1} \Leftrightarrow x = 1\)

Vậy tập nghiệm của phương trình là \(S = \left\{ { 1} \right\}\)

Câu d

\(lo{g_7}\left( {x - 1} \right)lo{g_7}x{\rm{ }} = {\rm{ }}lo{g_7}x\)

Điều kiện: 

\(\left\{ \begin{array}{l}
x - 1 > 0\\
x > 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x > 1\\
x > 0
\end{array} \right. \Leftrightarrow x > 1\)

\(\eqalign{
& lo{g_7}\left( {x - 1} \right)lo{g_7}x = lo{g_7}x \cr & \Leftrightarrow {\log _7}\left( {x - 1} \right).{\log _7}x - {\log _7}x = 0\cr 
& \Leftrightarrow {\log _7}x({\log _7}(x - 1) - 1) = 0 \cr 
& \Leftrightarrow \left[ \matrix{
{\log _7}x = 0 \hfill \cr 
{\log _7}(x - 1) = 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr 
x - 1 = 7 \hfill \cr} \right. \cr 
& \Leftrightarrow \left[ \matrix{
x = 1(loai) \hfill \cr 
x = 8(TM) \hfill \cr} \right. \cr}\)

Vậy phương trình đã cho có nghiệm là \(x = 8\)

Câu e

\({\log _3}x + {\log _{\sqrt 3 }}x + {\log _{{1 \over 3}}}x = 6\)

Điều kiện : \(x > 0\)

Ta có

\(\eqalign{
& {\log _3}x + {\log _{\sqrt 3 }}x + {\log _{{1 \over 3}}}x = 6 \cr} \)

\(\begin{array}{l}
\Leftrightarrow {\log _3}x + {\log _{{3^{1/2}}}}x + {\log _{{3^{ - 1}}}}x = 6\\
\Leftrightarrow {\log _3}x + 2{\log _3}x - {\log _3}x = 6\\
\Leftrightarrow 2{\log _3}x = 6\\
\Leftrightarrow {\log _3}x = 3\\
\Leftrightarrow x = {3^3} = 27
\end{array}\)

Vậy phương trình đã cho có nghiệm là: \(x = 27\)

Câu f

\(\log \displaystyle{{x + 8} \over {x - 1}} = \log x\)

Điều kiện: \(\left\{ \begin{array}{l}x > 0\\\dfrac{{x + 8}}{{x - 1}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\\left[ \begin{array}{l}x > 1\\x <  - 8\end{array} \right.\end{array} \right. \) \(\Leftrightarrow x > 1\)

Khi đó \(\log \dfrac{{x + 8}}{{x - 1}} = \log x \Leftrightarrow \dfrac{{x + 8}}{{x - 1}} = x\) \( \Rightarrow x + 8 = x\left( {x - 1} \right)\) \( \Leftrightarrow {x^2} - 2x - 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\left( {TM} \right)\\x =  - 2\left( L \right)\end{array} \right.\)

Vậy phương trình có nghiệm \(x = 4\).

Giải các bất phương trình

a) \({2^{2x - 1}} + {\rm{ }}2{^{2x - 2}} + {\rm{ }}{2^{2x - 3}} \ge {\rm{ }}448\)

b) \({\left( {0,4} \right)^x}-{\rm{ }}{\left( {2,5} \right)^{x + 1}} > {\rm{ }}1,5\)

c) \(log_3\left [ log_\frac{1}{2}(x^2-1) \right ]<1\)

d) \(log_{0,2}^2x-5log_{0,2}x < -6\)

Phương pháp giải

Vậy dụng các phương pháp giải bất phương trình mũ và lôgarit  đã học ở bài 6 chương 2 Giải tích 12

Hướng dẫn giải

Câu a

\(\displaystyle \begin{array}{l}a)\,\,\,{2^{2x - 1}} + {2^{2x - 2}} + {2^{2x - 3}} \ge 448\\\Leftrightarrow {2^{2x - 3}}{.2^2} + {2^{2x - 3}}{.2^1} + {2^{2x - 3}} \ge 448\\\Leftrightarrow {2^{2x - 3}}\left( {4 + 2 + 1} \right) \ge 448\\\Leftrightarrow {7.2^{2x - 3}} \ge 448\\\Leftrightarrow {2^{2x - 3}} \ge 64\\\Leftrightarrow 2x - 3 \ge {\log _2}64 = 6\\\Leftrightarrow x \ge \dfrac{9}{2}\end{array}\)

Vậy tập nghiệm của bất phương trình đã cho là: \(\displaystyle S=[{{9}\over {2}}; +∞)\).

Câu b

\({\left( {0,4} \right)^x}-{\rm{ }}{\left( {2,5} \right)^{x + 1}} > {\rm{ }}1,5\)

\(\Leftrightarrow \left ( \frac{2}{5} \right )^x-\left ( \frac{5}{2} \right )^{x+1}>\frac{3}{2} \Leftrightarrow \left ( \frac{2}{5} \right )^x-\frac{5}{2}.\left ( \frac{5}{2} \right )^x>\frac{3}{2}\)

Đặt \(\left ( \frac{2}{5} \right )^x=t\Rightarrow \left ( \frac{5}{2} \right )^x=\frac{1}{t}\)

Bất phương trình trở thành

\(t-\frac{5}{2}.\frac{1}{t}> \frac{3}{2}\Leftrightarrow t-\frac{5}{2t}>\frac{3}{2} \Leftrightarrow \frac{2t^2-3t-5}{2t}>0\)

\(\Leftrightarrow \frac{(2t-5)(t+1)}{2t}>0 \ (2)\)

Bảng xét dấu

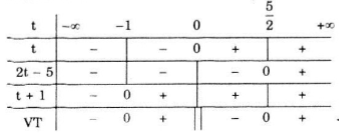
⇒ (2) có nghiệm -1 < t < 0 hoặc \(t> \frac{5}{2}\)

Với -1 < t < 0 thì \(-1 <\left ( \frac{2}{5} \right )^x<0\) (vô nghiệm)

Với \(t> \frac{5}{2}\) thì \(( \frac{2}{5})^x>\frac{5}{2}\Leftrightarrow \left ( \frac{2}{5} \right )^x> \left ( \frac{2}{5} \right )^{-1} \Leftrightarrow x<-1\)

Câu c

\(log_3\left [ log_\frac{1}{2}(x^2-1) \right ]<1\) (3)

ĐK: \(-\sqrt{2}

Khi đó: \((3)\Leftrightarrow log_{\frac{1}{2}}(x^2-1)<3\Leftrightarrow x^2-1> \frac{1}{8}\Leftrightarrow x^2> \frac{9}{8}\)

\(\Leftrightarrow \Bigg \lbrack \begin{matrix} x>\frac{3}{2\sqrt{2}}\\ \\ x< -\frac{3}{2\sqrt{2}} \end{matrix}\)

Kết hợp với điều kiện ta được nghiệm của bất phương trình là:

\(-\sqrt{2}

Câu d

\(log_{0,2}^2x-5log_{0,2}x < -6\)

ĐK: x >  0

Đặt log0,2 x = t.

Phương trình trở thành \(t^2-5t+6<0\Leftrightarrow 2

Với \(2

Kết hợp với điều kiện ta được nghiệm của bất phương trình trình là:

\(\frac{1}{125}< x< \frac{1}{25}\).

Tập xác định của hàm số \(y= log \frac{x-2}{1-x}\) là:

(A) (\(-\infty\), 1) ∪ (2, \(+\infty\))

(B) (1, 2)

(C) R\{1}

(D) R\{1, 2}

Phương pháp giải

Hàm số \(y = \log f\left( x \right)\) xác định \( \Leftrightarrow f\left( x \right) > 0\).

Hướng dẫn giải

Hàm số \(\displaystyle y = \log {{x - 2} \over {1 - x}}\) xác định \(\displaystyle \Leftrightarrow \dfrac{{x - 2}}{{1 - x}} > 0 \) \( \Leftrightarrow \left( {x - 2} \right)\left( {1 - x} \right) > 0 \) \(\Leftrightarrow \left( {x - 2} \right)\left( {x - 1} \right) < 0 \) \( \Leftrightarrow 1 < x < 2\)

Vậy tập nghiệm của bpt là (1; 2).

Chọn đáp án B.

Chọn khẳng định sai trong các khẳng định sau đây

(A) \(\ln x > 0 ⇔ x > 1\)

(B) \(\log_2x< 0 ⇔ 0< x < 1\)

(C) \({\log _{{1 \over 3}}}a > {\log _{{1 \over 3}}}b \Leftrightarrow a > b > 0\)

(D) \({\log _{{1 \over 2}}}a = {\log _{{1 \over 2}}}b \Leftrightarrow a = b > 0\)

Phương pháp giải

Sử dụng phương pháp giải bất phương trình logarit cơ bản:

\({\log _a}f\left( x \right) > {\log _a}g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
a > 1\\
f\left( x \right) > g\left( x \right) > 0
\end{array} \right.\\
\left\{ \begin{array}{l}
0 < a < 1\\
0 < f\left( x \right) < g\left( x \right)
\end{array} \right.
\end{array} \right.\)

Hướng dẫn giải

A. \(\ln x > 0 = \ln 1 \Leftrightarrow x > 1\) (do \(e > 1\) ) nên A đúng.

B. \({\log _2}x < 0 = {\log _2}1 \Leftrightarrow 0 < x < 1\) (do \(2>1\) ) nên B đúng.

C. \({\log _{\frac{1}{3}}}a > {\log _{\frac{1}{3}}}b\) \( \Leftrightarrow 0 < a < b\) (do \(0 < \dfrac{1}{3} < 1\)) nên C sai.

D. \({\log _{\frac{1}{2}}}a = {\log _{\frac{1}{2}}}b \Leftrightarrow a = b > 0 \) nên D đúng.

Chọn đáp án C.

Cho hàm số \(f\left( x \right){\rm{ }} = {\rm{ }}ln{\rm{ }}(4x{\rm{ }}-{\rm{ }}{x^2})\). Chọn khẳng định đúng trong các khẳng định sau đây

(A) \(f’ (2) = 1\)          (B). \(f’(2) = 0\)

(C) \(f’(5) = 1,2\)      (D).\(f’(-1) = -1,2\)

Phương pháp giải

Cách 1

Sử dụng MTCT.

Cách 2

Sử dụng công thức tính đạo hàm của hàm hợp: \(\left( {\ln u} \right)' = \dfrac{{u'}}{u}\).

Thay \(x = 2\) tính \(f'\left( 2 \right)\).

Hướng dẫn giải

Cách 1 

ĐK: \(4x - {x^2} > 0 \Leftrightarrow 0 < x < 4\).

Vì hàm số không xác định tại \(x = 5, x = -1\) nên (C) và (D) sai.

Sử dụng máy tính cầm tay tính f’(2) (nhập hàm và cho x = 2 ấn = ) ta được:

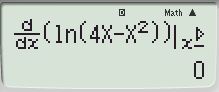
Vậy chọn (B).

Cách 2

\(\begin{array}{l}
f'\left( x \right) = \frac{{\left( {4x - {x^2}} \right)'}}{{4x - {x^2}}} = \frac{{4 - 2x}}{{4x - {x^2}}}\\
\Rightarrow f'\left( 2 \right) = \frac{{4 - 2.2}}{{4.2 - {2^2}}} = 0
\end{array}\)

Vậy chọn (B)

Cho hàm số \(g(x) = lo{g_{{1 \over 2}}}({x^2} - 5x + 7)\) . Nghiệm của bất phương trình là g(x) > 0 là:

(A) \(x > 3\)                (B) \(x < 2\) hoặc \(x > 3\)

(C) \(2 < x < 3\)        (D) \(x < 2\)

Phương pháp giải

Cách 1: Thử và loại các đáp án

Cách 2: Giải phương trình logarit cơ bản: \({\log _a}f\left( x \right) > b \Leftrightarrow \left\{ \begin{array}{l}0 < a < 1\\0 < f\left( x \right) < {a^b}\end{array} \right.\)

Hướng dẫn giải

Cách 1

Vì \(g(0) = {\log _{{1 \over 2}}}7 < 0\) nên (B) và (D) sai.

Mặt khác \(g(4) = {\log _{{1 \over 2}}}3 < 0\) nên (A) sai

Do đó chọn (C).

Cách 2

\({\log _{\frac{1}{2}}}\left( {{x^2} - 5x + 7} \right) > 0\) \(\Leftrightarrow 0 < {x^2} - 5x + 7 < {\left( {\frac{1}{2}} \right)^0} = 1\) \(\Leftrightarrow {x^2} - 5x + 7 < 1\)

(Do \({x^2} - 5x + 7 = {x^2} - 2.\dfrac{5}{2}.x + \dfrac{{25}}{4} + \dfrac{3}{4} \) \(= {\left( {x - \dfrac{5}{2}} \right)^2} + \dfrac{3}{4} > 0\)

\(\Leftrightarrow {x^2} - 5x + 6 < 0\) \(\Leftrightarrow 2 < x < 3.\)

Chọn đáp án C.

Trong các hàm số: \(\displaystyle f(x) = \ln {1 \over {{\mathop{\rm sinx}\nolimits} }},g(x) = \ln {{1 + {\mathop{\rm sinx}\nolimits} } \over {\cos x}},h(x) = \ln {1 \over {\cos x}}\)

Hàm số có đạo hàm là \(\displaystyle {1 \over {\cos x}}\)?

(A) \(\displaystyle f(x)\)                   (B) \(\displaystyle g(x)\)

(C) \(\displaystyle h(x)\)                   (D) \(\displaystyle g(x)\) và \(\displaystyle h(x)\)

Phương pháp giải

Sử dụng công thức tính đạo hàm của hàm hợp: \(\left( {\ln u} \right)' = \dfrac{{u'}}{u}\) lần lượt tính đạo hàm của các hàm số đã cho và kết luận.

Hướng dẫn giải

Ta có

\(\begin{array}{l}f\left( x \right) = \ln \dfrac{1}{{\sin x}} = \ln {\left( {\sin x} \right)^{ - 1}} = - \ln \sin x\\\Rightarrow f'\left( x \right) = - \dfrac{{\left( {\sin x} \right)'}}{{\sin x}} = \dfrac{{ - \cos x}}{{\sin x}} = - \cot x\\h\left( x \right) = \ln \dfrac{1}{{\cos x}} = \ln {\left( {\cos x} \right)^{ - 1}} = - \ln \cos x\\\Rightarrow h'\left( x \right) = - \dfrac{{\left( {\cos x} \right)'}}{{\cos x}} = - \dfrac{{ - \sin x}}{{\cos x}} = \tan x\end{array}\)

Do đó, (A), (C) và (D) sai

Chọn đáp án (B).

Số nghiệm của phương trình \({2^{2{x^2} - 7x + 5}} = 1\) là:

(A). 0          (B). 1           (C). 2           (D). 3

Phương pháp giải

Đưa về cùng cơ số 2. Ta có \({2^{f\left( x \right)}} = {2^{g\left( x \right)}} \Leftrightarrow f\left( x \right) = g\left( x \right).\)

Hướng dẫn giải

\(\begin{array}{l}\,\,\,\,\,{2^{2{x^2} - 7x + 5}} = 1\\\Leftrightarrow {2^{2{x^2} - 7x + 5}} = {2^0}\\\Leftrightarrow 2{x^2} - 7x + 5 = 0\\\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{5}{2}\\x = 1\end{array} \right.\end{array}\).

Vậy phương trình đã cho có 2 nghiệm \(x = \dfrac{5}{2};x = 1\).

Vậy chọn (C)

Nghiệm của phương trình \({10^{log9}} = {\rm{ }}8x{\rm{ }} + {\rm{ }}5\) là

A. \(0\)         B.  \(x = {1 \over 2}\)        (C). \({5 \over 8}\)       (D). \({7 \over 4}\)

Phương pháp giải

Sử dụng công thức \({a^{{{\log }_a}f\left( x \right)}} = f\left( x \right) > 0\)

Hướng dẫn giải

Vì \({10^{log9}} = {\rm{ }}9\) nên phương trình đã cho là \(9 = 8x + 5\).

\( \Leftrightarrow 8x = 4 \Leftrightarrow x = \frac{1}{2}\).

Phương trình này có nghiệm là  \(x = {1 \over 2}\)

Chọn đáp án (B)