Toán 12 Chương 3 Bài 2: Phương trình mặt phẳng

a) Biểu thức tọa độ tích có hướng

Cho hai vectơ \(\vec{a}=(x_1;y_1;z_1)\) và \(\vec{b}=(x_2;y_2;z_2)\), vectơ \(\overrightarrow n = \left[ {\overrightarrow a ;\overrightarrow b } \right]\) được gọi là tích có hướng của hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\) được xác định như sau:

\(\left[ {\vec a,\vec b} \right] = \left( {\left| {\begin{array}{*{20}{c}}
{{y_1}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {z_1}}\\
{{y_2}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {z_2}}
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
{{z_1}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {x_1}}\\
{{z_2}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {x_2}}
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
{{x_1}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {y_1}}\\
{{x_2}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {y_2}}
\end{array}} \right|} \right) = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\)

b) Tính chất 

Vectơ \(\overrightarrow n\) vuông góc với cả hai vectơ  \(\overrightarrow a\) và \(\overrightarrow b.\)

c) Ứng dụng của tích có hướng

Chứng minh tính đồng phẳng của vectơ:

\(\vec{a},\vec{b},\vec{c}\) không đồng phẳng khi và chỉ khi \(\left [ \vec{a},\vec{b} \right ].\vec{c}\neq 0.\) Suy ra 4 điểm A, B, C, D không đồng phẳng khi và chỉ khi \(\left [ \overrightarrow{AB},\overrightarrow{AC} \right ].\overrightarrow{AD}\neq 0\).

\(\vec{a},\vec{b},\vec{c}\) đồng phẳng khi và chỉ khi \(\left [ \vec{a},\vec{b} \right ].\vec{c}= 0\). Suy ra A, B, C, D đồng phẳng khi và chỉ khi \(\left [ \overrightarrow{AB};\overrightarrow{AC} \right ].\overrightarrow{AD}=0\).

Tính diện tích tam giác và hình bình hành:

Diện tích hình bình hành ABCD: \(S_{ABCD}=\left | \left [ \overrightarrow{AB};\overrightarrow{AC} \right ] \right |\).

Diện tích tam giác \(\Delta ABC\): \(S_{\Delta ABC}=\frac{1}{2}\left | \left [ \overrightarrow{AB};\overrightarrow{AC} \right ] \right |\).

a) Vectơ pháp tuyến của mặt phẳng

Cho mặt phẳng (P). Nếu vectơ \(\vec n\) khác \(\vec 0\) có giá vuông góc với (P) thì \(\vec n\) được gọi là Vectơ pháp tuyến của của (P).

b) Phương trình tổng quát của mặt phẳng

Phương trình tổng quát của mặt phẳng có dạng: \(Ax+By+Cz+D=0, \,\, A^2+B^2+C^2\neq 0)\).

Với \(\overrightarrow{n}=(A;B;C)\) là Vectơ pháp tuyến (VTPT).

c) Viết phương trình mặt phẳng khi biết Vectơ pháp tuyến và một điểm thuộc mặt phẳng đó

Mặt phẳng (P) đi qua điểm \({{M_0}({x_0};{y_0};{z_0})}\), nhận vectơ \({\vec n = (A;B;C)}\) làm VTPT có phương trình tổng quát là:

\(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)

d) Phương trình mặt phẳng theo đoạn chắn

Mặt phẳng (P) đi qua A(a;0;0), B(0;b;0), C(0;0;c) có phương trình tổng quát là: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\).

e) Một số cách xác định Vectơ pháp tuyến của mặt phẳng

Gọi \(\vec n\) là VTPT của mặt phẳng (P), giải sử tồn tại \(\vec u_1\) và \(\vec u_2\) sao cho \(\left.\begin{matrix} \vec{n}\perp \overrightarrow{u_1}\\ \vec{n}\perp \overrightarrow{u_2} \end{matrix}\right\}\) thì \(\vec{n}=\left [ \overrightarrow{u_1}; \overrightarrow{u_2} \right ]\) là một VTPT của mặt phẳng (P).

Mặt phẳng (ABC) có một VTPT \(\vec{n}=\left [ \overrightarrow{AB};\overrightarrow{AC} \right ]\).

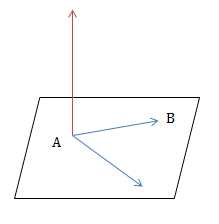
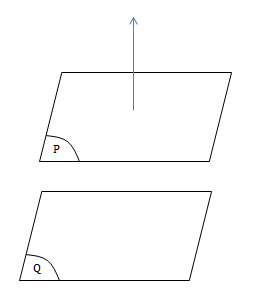
Mặt phẳng (P) song song với mặt phẳng (Q):

​Gọi: \(\overrightarrow{n}_P\) là một VTPT của (P), \(\overrightarrow{n}_Q\) là một VTPT của (Q) khi đó: \(\overrightarrow{n}_P=\overrightarrow{n}_Q.\)

Cho đường thẳng AB và mặt phẳng (P): \(\bigg \lbrack \begin{matrix} AB\subset (P)\\ AB //(P) \end{matrix}\) thì \(\vec{n_P}\perp \overrightarrow{AB}.\)

Nếu \((P)\perp (Q)\) thì \(\overrightarrow{n}_P\perp \overrightarrow{n}_Q\).

Cho hai mặt phẳng \((\alpha _1) \ A_1x+B_1y+C_1z+D_1=0\) có một VTPT \(\vec{n_1}=(A_1;B_1;C_1)\) và \((\alpha _2) \ A_2x+B_2y+C_2z+D_2=0\) có một VTPT \(\vec{n_2}=(A_2;B_2;C_2)\).

Khi đó vị trí tương đối giữa \((\alpha_1)\) và \((\alpha_2)\) được xác định như sau:

\((\alpha _1)//(\alpha _2)\) khi và chỉ khi \(\left\{\begin{matrix} \vec{n_1}=k.\vec{n_2}\\ D_1\neq D_2 \end{matrix}\right.\).

Nếu \(A_2, B_2, C_2, D_2 \neq 0\): \((\alpha _1)//(\alpha _2)\Leftrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}\neq \frac{D_1}{D_2}\).

\((\alpha _1)\equiv (\alpha _2)\) khi và chỉ khi  \(\left\{\begin{matrix} \vec{n_1}=k.\vec{n_2}\\ D_1=k. D_2 \end{matrix}\right.\).

Nếu \(A_2, B_2, C_2, D_2 \neq 0\) thì \((\alpha _1)\equiv (\alpha _2)\Leftrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}= \frac{D_1}{D_2}\).

\((\alpha _1),(\alpha _2)\) cắt nhau khi và chỉ khi \(\vec{n_1}\neq k.\vec{n_2}\).

Cho mặt phẳng (P): \(Ax+By+Cz+D=0 \ \ (A^2+B^2+C^2\neq 0)\)
và điểm \(M(x_0,y_0,z_0)\).
Khoảng cách từ M đến (P) được xác định bởi công thức: \(d(M;(P))=\frac{\left | Ax_0+Ay_0+Az_0+D \right |}{\sqrt{A^2+B^2+C^2}}\).

​Nếu \(A_2,B_2,C_2\neq 0\) thì \((\alpha _1),(\alpha _2)\) cắt nhau \(\Leftrightarrow \Bigg \lbrack\begin{matrix} \frac{A_1}{A_2} \neq \frac{B_1}{B_2}\\ \frac{A_1}{A_2} \neq \frac{C_1}{C_2}\\ \frac{B_1}{B_2} \neq \frac{C_1}{C_2} \end{matrix}\).

Cho hai mặt phẳng \((P)\;{A_1}x + {B_1}y + {C_1}z + {D_1} = 0\) và \((Q)\;{A_2}x + {B_2}y + {C_2}z + {D_2} = 0\) có VTPT lần lượt là:

\(\vec{n}_P=(A_1;B_1;C_1)\) và \(\vec{n}_Q=(A_2;B_2;C_2)\), khi đó:

​\(cos\widehat {(P,Q)} = \left| {cos({{\vec n}_P};{{\vec n}_Q})} \right| = \frac{{\left| {{{\vec n}_P}.{{\vec n}_Q}} \right|}}{{\left| {{{\vec n}_P}} \right|\left| {{{\vec n}_Q}} \right|}}\)\(=\frac{\left | A_1B_2+B_1B_2+C_1C_2 \right |}{\sqrt{A^2_1+B_1^2+C^2_1} .\sqrt{A^2_2+B_2^2+C^2_2}}\)

Chú ý

\(0^0\leq (\widehat{P,Q})\leq 90^0\).

\((P)\perp (Q)\Leftrightarrow \vec{n}_P.\vec{n}_Q\)\(\Leftrightarrow A_1A_2+B_1B_2+C_1C_2=0\).

Câu 1: Cho ba điểm A(2;0;0), B(0;3;1), C(-1;4;2).

a) Chứng minh: A,B,C là 3 đỉnh của một tam giác

b) Tính diện tích tam giác ABC.

c) Tính độ dài đường cao kẻ từ đỉnh A của tam giác ABC.

Hướng dẫn giải

a) Ta có \(\overrightarrow {AB} ( - 2;3;1),\overrightarrow {AC} ( - 3;4;2) \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = (2;1;1) \ne \overrightarrow 0\) nên \(\overrightarrow {AB} ,\overrightarrow {AC}\) không cùng phương do đó A, B, C tạo thành 3 đỉnh của tam giác.

b) \({S_{ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right| = \frac{{\sqrt 6 }}{2}\).

c) \(AH = \frac{{2{S_{\Delta ABC}}}}{{BC}} = \frac{{\sqrt 6 }}{{\sqrt {{1^2} + {{(4 - 3)}^2} + {{(2 - 1)}^2}} }} = \sqrt 2\).

Câu 2: Cho 4 điểm: A(1;0;1), B(-1;1;2), C(-1;1;0), D(2;-1;-2)

a) Chứng minh rằng: A,B,C,D là 4 đỉnh của một tứ diện.

c) Tính độ dài đường cao AH của tứ diện ABCD.

Hướng dẫn giải

a) Ta có: \(\overrightarrow {AB} = \left( { - 2;1;1} \right);\) \(\overrightarrow {AC} = \left( { - 2;1; - 1} \right)\,;\,\overrightarrow {AD} = \left( {1; - 1; - 3} \right).\)

\(\left[ {\overrightarrow {AC} ;\overrightarrow {AC} } \right].\overrightarrow {AD} = 2 \ne 0.\)

Vậy 4 điểm A,B,C,D không đồng phẳng.

Suy ra A,B,C,D là 4 đỉnh của một tứ diện.

b) \({V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right]\overrightarrow {AD} } \right| = \frac{1}{3}\) 

Mà: \({V_{ABCD}} = \frac{1}{3}.{S_{BCD}}.AH \Rightarrow AH = \frac{1}{{{S_{BCD}}}}.\)   

\(\left[ {\overrightarrow {BC} ;\overrightarrow {CD} } \right] = \left( { - 4; - 6;0} \right) \Rightarrow {S_{BCD}} = \frac{1}{2}\left| {\left[ {\overrightarrow {BC} ;\overrightarrow {CD} } \right]} \right| = \sqrt {13} .\)

Vậy: \(AH = \frac{1}{{\sqrt {13} }}.\)   

Câu 1: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) trong các trường hợp sau:

a) (P) đi qua điểm \({M_0}( - 2;3;1)\) và vuông góc với đường thẳng AB với \(A(3;1; - 2):B(4; - 3;1).\)

b) (P) đi qua điểm \({M_0}( - 2;3;1)\) và song song với mặt phẳng (Q): \(4x - 2y + 3z - 5 = 0.\)  

c) (P) đi qua điểm \({M_0}( - 2;3;1)\) và vuông góc với hai mặt phẳng (Q): x-3y+2z-1=0; (R): 2x+y-z-1=0.

d) (P) đi qua 3 điểm \(A(2;0; - 1);B(1; - 2;3);C(0;1;2).\)

Hướng dẫn giải

a) Mặt phẳng (P) có VTPT \(\overrightarrow n = \overrightarrow {AB} = (1; - 4;3).\)

Do (P) đi qua \({M_0}( - 2;3;1)\) nên có phương trình là:

\(1(x + 2) - 4(y - 3) + 3(z - 1) = 0\)\(\Leftrightarrow (P):x - 4y + 3z + 11 = 0.\)  

b) (P)//(Q)\(\Rightarrow VTPT\overrightarrow {{n_(}_{P)}} = VTPT{\overrightarrow n _{(Q)}} = (4; - 2;3).\) 

\((P):4(x + 2) - 2(y - 3) + 3(z - 1) = 0 \Leftrightarrow (P):4x - 2y + 3z + 11 = 0.\)

c) Ta có: \({\left. {\begin{array}{*{20}{l}} {(P) \bot (Q) \Rightarrow VTPT\overrightarrow {{n_{(P)}}} \bot VTPT\overrightarrow {{n_{(Q)}}} = (1; - 3;2)}\\ {(P) \bot (Q) \Rightarrow VTPT\overrightarrow {{n_{(P)}}} \bot VTPT\overrightarrow {{n_{(R)}}} = (2;1; - 1)} \end{array}} \right\}}\)

Suy ra mặt phẳng (P) có VTPT là: \({\overrightarrow {{n_{(P)}}} = \left[ {\overrightarrow {{n_{(Q)}}} ,\overrightarrow {{n_{(R)}}} } \right] = (1;5;7)}.\)

Mặt khác (P) đi qua \({M_0}( - 2;3;1)\) nên có phương trình là:

\((P):(x + 2) + 5(y - 3) + 7(z - 1) = 0 \Leftrightarrow (P):z + 5y + 7z - 20 = 0.\)

d) Cặp VTCP mặt phẳng (P) là:

\(\left\{ \begin{array}{l} \overrightarrow {AB} = ( - 1; - 2;4)\\ \overrightarrow {AC} = ( - 2;1;3) \end{array} \right. \Rightarrow VTPT\overrightarrow {{n_{(P)}}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = ( - 10; - 5; - 5).\)

Mặt khác (P) đi qua A(2;0;-1) nên có phương trình là:

 \((P): - 10(x - 2) - 5(y - 0) - 5(z + 1) = 0 \Leftrightarrow (P):2x + y + z - 3 = 0.\)

Câu 2: Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình sau:

a) 2x-3y+4z-4=0 và 3x-y-x-1=0.

b) -x+y-z+4=0 và 2x-2y+2z-7=0.

c) 3x+3y-6z-12=0 và 4x+4y-8z-16=0.

Hướng dân giải

a) Ta có: \(\frac{2}{3} \ne \frac{{ - 3}}{{ - 1}} \ne \frac{4}{1}\) vậy hai mặt phẳng cắt nhau.

b) Ta có: \(\frac{{ - 1}}{2} = \frac{1}{{ - 2}} = \frac{{ - 1}}{2} \ne \frac{4}{7}\) vậy hai mặt phẳng song song.

c) Ta có: \(\frac{3}{4} = \frac{3}{4} = \frac{{ - 6}}{{ - 8}} = \frac{{ - 12}}{{ - 16}}\) vậy hai mặt phẳng trùng nhau.

Câu 3: Cho hai mặt phẳng có phương trình lần lượt là: \(\left( {{m^2} - 5} \right)x - 2y + mz + m - 5 = 0\) và \(x + 2y - 3nz + 3 = 0.\)  

Tìm m và n để hai mặt phẳng trùng nhau.

Hướng dẫn giải

Hai mặt phẳng trùng nhau khi và chỉ khi:

\(\begin{array}{l} \frac{{{m^2} - 5}}{1} = \frac{{ - 2}}{2} = \frac{m}{{ - 3n}} = \frac{{m - 5}}{3}\\ \Leftrightarrow \left\{ \begin{array}{l} {m^2} - 5 = - 1\\ m = 3n\\ m - 5 = - 3 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m = \pm 2\\ n = \frac{m}{3}\\ m = 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m = 2\\ n = \frac{2}{3} \end{array} \right. \end{array}\)

Vậy với m=2; \(n=\frac{2}{3}\) thì hai mặt phẳng trùng nhau.

Câu 4: Tìm khoảng cách từ các điểm \({M_0}\left( {1; - 1;2} \right);\,{M_1}\left( {3;4;1} \right);\,{M_2}\left( { - 1;4;3} \right)\) đến mặt phẳng x+2y+2z-10=0.

Hướng dẫn giải

\(\begin{array}{l} d\left( {{M_0},(P)} \right) = \frac{{\left| {1 + 2.( - 1) + 2.2 - 10} \right|}}{{\sqrt {{1^2} + 2{}^2 + {2^2}} }} = \frac{7}{3}\\ d\left( {{M_1},(P)} \right) = \frac{{\left| {3 + 2.4 + 2.1 - 10} \right|}}{{\sqrt {{1^2} + 2{}^2 + {2^2}} }} = 1\\ d\left( {{M_2},(P)} \right) = \frac{{\left| { - 1 + 2.4 + 2.3 - 10} \right|}}{{\sqrt {{1^2} + 2{}^2 + {2^2}} }} = 1 \end{array}\)

Câu 1: Viết phương trình mặt phẳng \((\alpha )\) trong các trường hợp sau:

a) \((\alpha )\) đi qua điểm M(2;0; 1) và nhận \(\overrightarrow n  = (1;1;1)\) làm vecto pháp tuyến;

b) \((\alpha )\) đi qua điểm A(1; 0; 0) và song song với giá của hai vecto \(\overrightarrow u  = (0;1;1),\overrightarrow v  = ( - 1;0;2)\);

c) \((\alpha )\) đi qua ba điểm M(1;1;1), N(4; 3; 2), P(5; 2; 1)

Câu 2: Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(1; -2; 4), B(3; 6; 2).

Câu 3: Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0 ; 4), D(4; 0 ; 6)

a) Hãy viết phương trình mặt phẳng (ABC).

b) Hãy viết phương trình mặt phẳng \((\alpha )\) đi qua điểm D và song song với mặt phẳng (ABC).

Câu 4: Hãy viết phương trình mặt phẳng \((\alpha )\) đi qua gốc tọa độ O(0; 0; 0) và song song với mặt phẳng \((\beta )\) : x + y + 2z – 7 = 0.

Câu 5: Lập phương trình mặt phẳng \((\alpha )\) đi qua hai điểm A(0; 1; 0) , B(2; 3; 1) và vuông góc với mặt phẳng \((\beta )\) : x + 2y – z = 0 .

Câu 6: Xác định các giá trị của A, B để hai mặt phẳng sau đây song song với nhau:

\((\alpha )\) : Ax – y + 3z + 2 = 0

\((\beta )\):  2x + By + 6z + 7 = 0

Câu 1: Trong không gian Oxyz, cho các điểm \(A\left( {1;2;3} \right);B\left( {0;0;2} \right);C\left( {1;0;0} \right);D\left( {0; - 1;0} \right)\). Tính thể tích khối tứ diện ABCD.

A. 1

B.  \(\frac{1}{6}\)

C.  \(\frac{1}{3}\)

D. \(\frac{1}{2}\)

Câu 2: Trong không gian với hệ trục \(Oxyz\), viết phương trình mặt phẳng chứa hai điểm \(A(1;0;1)\), \(B(-1;2;2)\) và song song với trục \(Ox\).

A. \(x + y - z = 0\)

B. \(2y - z + 1 = 0\)

C. \(y - 2z + 2 = 0\)

D. \(x + 2z - 3 = 0\)

Câu 3: Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A(1;1;1)\) và \(B(1;3;-5)\) Viết phương trình mặt phẳng trung trực của AB.

A.  \(y - 3z + 4 = 0\)

B.  \(y - 3z - 8 = 0\)

C.  \(y - 2z -6 = 0\)  

D.  \(y - 2z + 2 = 0\)

Câu 4: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( \alpha \right):2x + my + 3z - 5 = 0\) và \(\left( \beta \right):nx - 8y - 6z + 2 = 0\left( {m,n \in \mathbb{R} } \right)\) . Tìm giá trị của m và n để hai mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau?

A.  \(n=m=-4\) 

B.  \(n=-4; m=4\)

C.  \(n=m=4\) 

D. \(n=4;m=-4\)

A.  \(d\left( {A,\left( {SMN} \right)} \right) = 4\)

B.  \(d\left( {A,\left( {SMN} \right)} \right) = 2\)

C.  \(d\left( {A,\left( {SMN} \right)} \right) = \sqrt 2\)

D.  \(d\left( {A,\left( {SMN} \right)} \right) = 1\)

Qua bài học này học sinh nắm được một số nội dung chính như sau:

•  Biết dạng phương trình mặt phẳng trong không gian, viết được phương trình mặt phẳng.
• Biết công thức tính khoảng cách từ 1 điểm đến 1 mặt phẳng và xác định được vectơ pháp tuyến của mặt phẳng
•  Viết phương trình mặt phẳng, tính khoảng cách từ 1 điểm đến 1 mp