Toán 12 Chương 1 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Cho hàm số \(y = f\left( x \right)\) xác định trên miền \(D\).

• Số \(M\) được gọi là giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên \(D\) nếu \(\left\{ \begin{array}{l}f\left( x \right) \le M,\forall x \in D\\\exists {x_0} \in D,f\left( {{x_0}} \right) = M\end{array} \right.\) Kí hiệu \(M = \mathop {\max }\limits_{x \in D} f\left( x \right)\) hoặc \(M = \mathop {\max }\limits_D f\left( x \right)\)
• Số \(m\) được gọi là giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(D\) nếu \(\left\{ \begin{array}{l}f\left( x \right) \ge m,\forall x \in D\\\exists {x_0} \in D,f\left( {{x_0}} \right) = m\end{array} \right.\) Kí hiệu \(m = \mathop {\min }\limits_{x \in D} f\left( x \right)\) hoặc \(m = \mathop {\min }\limits_D f\left( x \right)\)

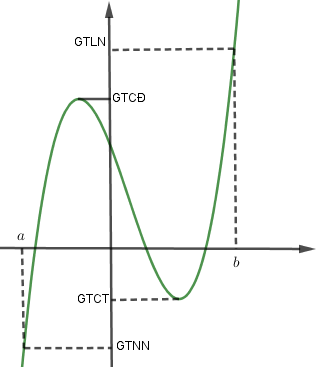
(Cần chú ý phân biệt GTLN, GTNN với cực đại, cực tiểu của hàm số, dưới đây là hình vẽ minh họa GTLN, GTNN của hàm số trên đoạn $[a;b]$ để các em phân biệt.)

a) Dạng 1: Tìm GTLN, GTNN của hàm số trên một đoạn

Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ {a;b} \right]\)

Phương pháp

- Bước 1: Tính \(y'\), giải phương trình \(y' = 0\) tìm các nghiệm \({x_1},{x_2},...{x_n}\) thỏa mãn \(a \le {x_1} < {x_2} < ... < {x_n} \le b\)

- Bước 2: Tính các giá trị \(f\left( a \right),f\left( {{x_1}} \right),...,f\left( {{x_n}} \right),f\left( b \right)\)

- Bước 3: So sánh các giá trị tính được ở trên và kết luận:

• Giá trị lớn nhất tìm được trong số các giá trị ở trên là GTLN \(M\) của hàm số trên \(\left[ {a;b} \right]\)
• Giá trị nhỏ nhất tìm được trong số các giá trị ở trên là GTNN \(m\) của hàm số trên \(\left[ {a;b} \right]\)

b) Dạng 2: Tìm GTLN, GTNN của hàm số trên một khoảng.

Cho hàm số \(y = f\left( x \right)\) xác đinh và liên tục trên \(\left( {a;b} \right)\)

Phương pháp

- Bước 1: Tính \(f'\left( x \right)\), giải phương trình \(y' = 0\) tìm các nghiệm \({x_1},{x_2},...{x_n}\) thỏa mãn \(a \le {x_1} < {x_2} < ... < {x_n} \le b\)

- Bước 2: Tính các giá trị \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right)\) và \(A = \mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right);B = \mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right)\)

- Bước 3: So sánh các giá trị tính được và kết luận.

• Nếu GTLN (hoặc GTNN) trong số các giá trị ở trên là \(A\) hoặc \(B\) thì kết luận hàm số không có GTLN (hoặc GTNN) trên khoảng \(\left( {a;b} \right)\)
• Nếu GTLN (hoặc GTNN) trong số các giá trị ở trên là \(f\left( {{x_i}} \right),i \in \left\{ {1;2;...;n} \right\}\) thì kết luận hàm số đạt GTLN (hoặc GTNN) bằng \(f\left( {{x_i}} \right)\) khi \(x = {x_i}\)

c) Dạng 3: Tìm điều kiện của tham số để hàm số có GTLN, GTNN thỏa mãn điều kiện cho trước

Cho hàm số \(f\left( x \right)\) xác đinh và liên tục trên đoạn \(\left[ {a;b} \right]\)

Phương pháp: (chỉ áp dụng cho một số bài toán dễ dàng tìm được nghiệm của \(y'\))

• Bước 1: Tính \(y'\), giải phương trình \(y' = 0\) tìm các nghiệm \({x_1},{x_2},...{x_n}\)
• Bước 2: Tính các giá trị \(f\left( a \right),f\left( {{x_1}} \right),...,f\left( {{x_n}} \right),f\left( b \right)\)
• Bước 3: Biện luận theo tham số để tìm GTLN, GTNN của hàm số trên đoạn \(\left[ {a;b} \right]\)
• Bước 4: Thay vào điều kiện bài cho để tìm \(m\)

Tìm GTLN-GTNN của các hàm số: \(y = f\left( x \right) = - \frac{1}{3}{x^3} + {x^2} - 2x + 1\) trên đoạn \(\left[ { - 1;0} \right]\).

Hướng dẫn giải

Hàm số \(y = f\left( x \right) = - \frac{1}{3}{x^3} + {x^2} - 2x + 1\) xác định trên đoạn \(\left[ { - 1;0} \right]\).

• \({f^/}\left( x \right) = - {x^2} + 2x - 2\)
• \({f^/}\left( x \right) = 0 \Leftrightarrow - {x^2} + 2x - 2 = 0\)
• Ta có: \(f\left( { - 1} \right) = \frac{{11}}{3};f\left( 0 \right) = 1\).
• Vậy: \(\mathop {\max f\left( x \right)}\limits_{\left[ { - 1;0} \right]} = \frac{{11}}{3}\); \(\mathop {\min f\left( x \right)}\limits_{\left[ { - 1;0} \right]} = 1\)

Tìm GTLN-GTNN của các hàm số: \(y=\frac{x^2+2x+3}{x-1},x\in(1;3].\)

Hướng dẫn giải

Xét hàm số \(y=\frac{x^2+2x+3}{x-1}\) xác định trên \((1;3].\)

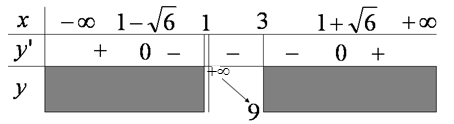
• Vậy hàm số có giá trị nhỏ nhất \(\mathop {Min}\limits_{x \in (1;3]} y = 9\), hàm số không có giá trị lớn nhất.

Cho hàm số \(y = \frac{{x - {m^2}}}{{x + 8}}\) với m là tham số thực. Tìm giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 3] bằng -2.

Hướng dẫn giải

TXĐ: \(D{\rm{ }} = {\rm{ }}R\backslash \left\{ { - 8} \right\}\)

Ta có: \(y' = \frac{{8 + {m^2}}}{{{{(x + 8)}^2}}} > 0\;\;\forall x\; \ne \; - 8\)

Khi đó: \(\mathop {\min }\limits_{{\rm{[}} - 1;1]} y = y(0) =  - \frac{{{m^2}}}{8} =  - 2 \Leftrightarrow {m^2} = 16 \Leftrightarrow m =  \pm 4\)

Câu 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau

a) f(x) = -3x² + 4x – 8 trên đoạn [0; 1]

b) f(x) = x³ + 3x² – 9x – 7 trên đoạn [-4; 3]

c) \(f(x) = \sqrt {25 - {x^2}} \) trên đoạn [-4; 4]

Câu 2: Tìm giá trị lớn nhất, nhỏ nhất của các hàm số sau

a) \(y=\dfrac{x}{4+x^2}\) trên khoảng \((-\infty;+\infty)\)

b) \(y=\dfrac{1}{\cos x}\) trên khoảng \(\left( \dfrac{\pi}{2};\dfrac{3\pi}{2} \right)\)

Câu 3: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x)=x+\dfrac{9}{x}\) trên đoạn [2;4]

Câu 4: Tìm các giá trị của tham số m để phương trình \(x^3-3x^2-m=0\) có ba nghiệm phân biệt

Câu 5: Cho số dương m. Hãy phân tích m thành tổng của hai số dương sao cho tích của chúng là lớn nhất

Câu 1: Giá trị lớn nhất của hàm số \(y=-x^2+4x-5\) trên đoạn [0;3] bằng

Câu 2: Giá trị nhỏ nhất của hàm số \(f(x)=x^3+3x^2-9x-7\) trên đoạn [-4;3] bằng: 

Câu 3: Tìm giá trị nhỏ nhất m của hàm số \(y = \log _2^2x - 4{\log _2}x + 1\) trên đoạn [1;8].

A. m=-2

B. m=1

C. m=-3

D. m=-5

Câu 4: Gọi M và m lần lượt là GTLN và GTNN của hàm số \(y = x\sqrt {1 - {x^2}}\) trên tập xác định. Tính M-m.

A. 1

B. 2

C. 3

D. 4

Câu 5: Tìm giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 6\) trên \(\left[ { - 4;4} \right]\).

A. \(\mathop {Min}\limits_{\left[ { - 4;4} \right]} y = 21\)

B. \(\mathop {Min}\limits_{\left[ { - 4;4} \right]} y = - 14\)

C. \(\mathop {Min}\limits_{\left[ { - 4;4} \right]} y = 11\)

D. \(\mathop {Min}\limits_{\left[ { - 4;4} \right]} y = - 70\)

Qua bài học này giúp các em:

• Hiểu được GTLN và GTNN của hàm số trên đoạn của một số hàm thường gặp.
• Nắm được các phương pháp tìm GTLN và GTNN của một số hàm số có đạo hàm trên một khoảng, một đoạn.