Giải bài tập SGK Toán 7 Ôn tập chương 3: Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác
Hướng dẫn Giải bài tập SGK Toán 7 Bài Ôn tập chương 3: Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 63 trang 87 SGK Toán 7
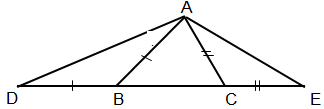
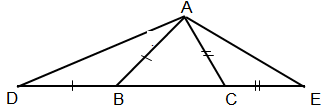
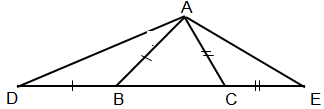
Cho tam giác \(ABC\) với \(AC < AB.\) Trên tia đối của tia \(BC\) lấy điểm \(D\) sao cho \(BD = AB.\) Trên tia đối của tia \(CB\) lấy điểm \(E\) sao cho \(CE = AC.\) Vẽ các đoạn thẳng \(AD, AE.\)
a) Hãy so sánh góc \(ADC\) và góc \(AEB.\)
b) Hãy so sánh các đoạn thẳng \(AD\) và \(AE.\)
Phương pháp giải
Áp dụng quan hệ giữa góc và cạnh đối diện trong tam giác:Trong một tam giác, cạnh đối diện góc lớn hơn thì lớn hơn và ngược lại góc đối diện cạnh lớn hơn thì lớn hơn.
Hướng dẫn giải
Câu a: Xét \(ΔABC\) có \(AC < AB\) (giả thiết)
\(⇒ \widehat {ABC} < \widehat {ACB}\) (quan hệ giữa cạnh và góc đối diện trong tam giác) (1)
\(ΔABD\) cân tại \(B\) vì \(AB = BD\) (giả thiết)
\(⇒ \widehat {ADB} = \widehat {DAB}\) (tính chất)
Mà \(\widehat {ABC} = \widehat {ADB} + \widehat {DAB}\) (góc ngoài tam giác)
⇒ \(\widehat {DAB} = \widehat {ADB} = \dfrac{\widehat {ABC}}{2} \) (2)
\(ΔACE\) cân tại \(C\) vì \(CA = CE\) (giả thiết)
\(⇒ \widehat {CAE} = \widehat {CEA}\) (tính chất)
Mà \(\widehat {ACB} = \widehat {CAE} + \widehat {CEA}\) (góc ngoài tam giác)
⇒ \(\widehat {CAE} = \widehat {CEA} = \dfrac{\widehat {ACB}}{2}\) (3)
Từ (1), (2), (3) suy ra \(\widehat {ADB} < \widehat {AEC}\)
hay \(\widehat {ADC} < \widehat {AEB}\) (điều phải chứng minh).
Câu b: Xét \(ΔADE\) có \(\widehat {ADE} < \widehat {AED}\) (chứng minh ở phần a)
Mà \(AE\) là cạnh đối diện \(\widehat {ADE}\) và \(AD\) là cạnh đối diện \(\widehat {AED}\)
\( \Rightarrow AE < AD\) (Quan hệ giữa góc - cạnh đối diện trong tam giác).
2. Giải bài 64 trang 87 SGK Toán 7
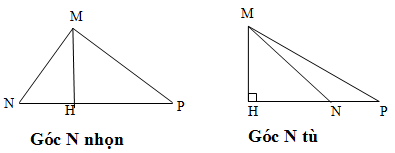
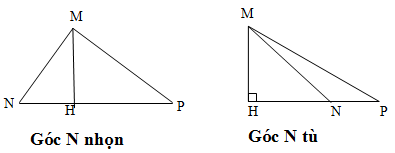
Gọi \(MH\) là đường cao của tam giác \(MNP.\) Chứng minh rằng: Nếu \(MN < MP\) thì \(HN < HP\) và \(\widehat {NMH} < \widehat {PMH}\) (yêu cầu xét hai trường hợp: khi góc \(N\) nhọn và khi góc \(N\) tù).
Phương pháp giải
- Áp dụng quan hệ giữa các đường xiên và hình chiếu:
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng thẳng đến đường thẳng thẳng đó:
- Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
- Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
- Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
- Áp dụng quan hệ giữa cạnh và góc trong tam giác: Trong một tam giác, cạnh đối diện góc lớn hơn thì lớn hơn và ngược lại góc đối diện cạnh lớn hơn thì lớn hơn.
Hướng dẫn giải
- Nếu góc \(N\) nhọn (hình a)
\(∆MNP\) có \(\hat N\) nhọn nên chân đường cao \(H\) kẻ từ \(M\) nằm giữa \(N\) và \(P.\)
Ta có hình chiếu của \(MN\) và \(MP\) lần lượt là \(HN\) và \(HP.\)
Từ giả thiết \(MN < MP\) \( \Rightarrow HN < HP\) (quan hệ giữa các đường xiên và hình chiếu).
\(∆MNP\) có \(MN < MP\) \( \Rightarrow\) \(\widehat {MPN} < \widehat {MNP}\) (quan hệ giữa cạnh và góc trong tam giác) (1)
Lại có
\(\widehat {NMH} + \widehat {MNH} = {90^o}\) (\(∆MNH\) vuông tại \(H\)) (2)
\(\widehat {MPH} + \widehat {PMH} = {90^o}\) (\(∆MHP\) vuông tại \(H\)) (3)
Từ (1), (2), (3) suy ra \(\widehat {NMH} < \widehat {PMH}\)
(Giải thích nếu tổng của hai cặp số cùng bằng nhau (bằng \( 90^o\) chẳng hạn) thì số nào cộng với số lớn hơn thì nhỏ hơn số kia. Tức là:
\(a + b = 90^o ; \quad \quad c + d = 90^o\)
mà \(b > d\) thì suy ra \(a < c\))
- Nếu góc \(N\) tù (hình b)
\(∆MNP\) có \(\hat N\) tù nên chân đường cao \(H\) ở ngoài cạnh \(NP\) và \(N\) ở giữa \(H\) và \(P\) (xem lại chứng minh bài 58 trang 83 SGK toán 7 tập 2)
\( \Rightarrow HN < HP.\)
Vì \(N\) ở giữa \(H\) và \(P\) nên tia \(MN\) ở giữa hai tia \(MH\) và \(MP.\) Từ đó suy ra \(\widehat {HMN} < \widehat {HMP}\).
3. Giải bài 65 trang 87 SGK Toán 7
Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài như sau: \(1\,cm, 2\,cm, 3\,cm, 4\,cm\) và \(5\,cm\)?
Phương pháp giải
Áp dụng: Trong một tam giác, độ dài một cạnh lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại.
Hướng dẫn giải
Để tạo được một tam giác thì độ dài ba cạnh phải thoả mãn bất đẳng thức tam giác đó là độ dài một cạnh lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại.
Vì vậy chỉ có bộ ba độ dài sau thoả mãn \((2\,cm; 3\,cm; 4\,cm);\) \((2\,cm; 4\,cm ; 5\,cm);\) \((3\,cm; 4\,cm; 5\,cm).\)
(Lưu ý: để xét cho nhanh, các bạn áp dụng phần Lưu ý (trang 63 sgk Toán 7 Tập 2), tức là ta so sánh độ dài lớn nhất với tổng hai cạnh hoặc so sánh độ dài nhỏ nhất với hiệu hai cạnh)
Thật vậy, ta có:
Vì \(3-2<4<3+2\) nên vẽ được tam giác có ba cạnh có độ dài là \(2\,cm; 3\,cm; 4\,cm\)
Vì \(4-2<5<4+2\) nên vẽ được tam giác có ba cạnh có độ dài là \(2\,cm; 4\,cm; 5\,cm\)
Vì \(4-3<5<4+3\) nên vẽ được tam giác có ba cạnh có độ dài là \(3\,cm; 4\,cm; 5\,cm\)
Với các bộ ba số khác đều không thỏa mãn bất đẳng thức tam giác.
Ví dụ với bộ ba độ dài \((1\,cm; 2\,cm; 3\,cm)\) không là ba cạnh của tam giác vì:
\(3 = 2 + 1\) mâu thuẫn với bất đẳng thức tam giác.
\(3 - 2 < 1\) mâu thuẫn với bất đẳng thức tam giác.
4. Giải bài 66 trang 87 SGK Toán 7
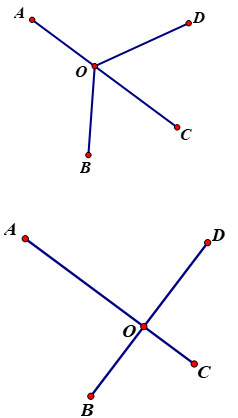
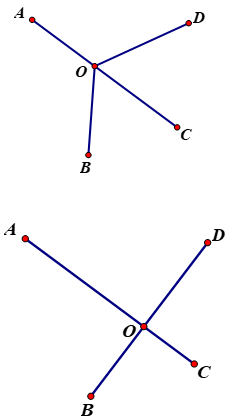
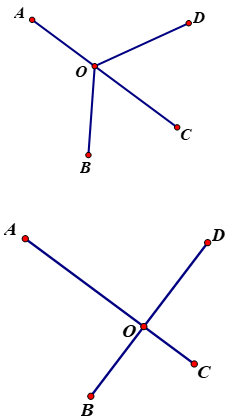
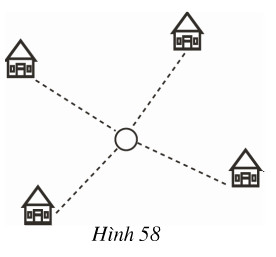
Đố: Bốn điểm dân cư được xây dựng như hình \(58\). Hãy tìm vị trí đặt một nhà máy sao cho tổng các khoảng cách từ nhà máy đến bốn điểm dân cư này là nhỏ nhất.
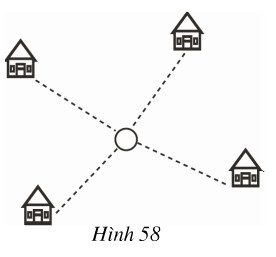
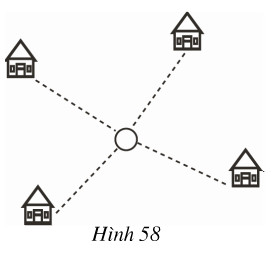
Phương pháp giải
Áp dụng bất đẳng thức trong tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Hướng dẫn giải
Gọi O là địa điểm đặt nhà máy (O tùy ý)
A, B, C, D lần lượt là bốn điểm dân cư (A,B, C, D cố định).
Ta luôn có:
OA + OC ≥ AC
OB + OD ≥ BD
⇒ OA + OB + OC + OD ≥ AC + BD (AC + BD là hằng số)
Vậy để OA + OB + OC + OD nhỏ nhất thì OA + OC = AC và OB + OD = BD.
OA + OC = AC khi O thuộc đoạn AC.
OB + OD = BD khi O thuộc đoạn BD.
Vậy OA + OB + OC + OD nhỏ nhất khi O là giao điểm của hai đoạn AC và BD.
5. Giải bài 67 trang 87 SGK Toán 7
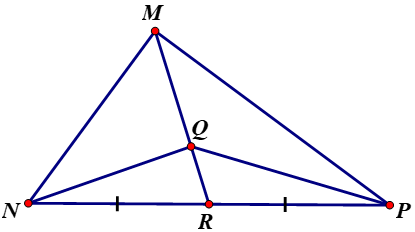
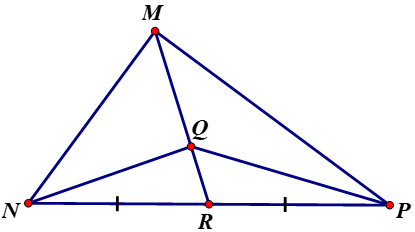
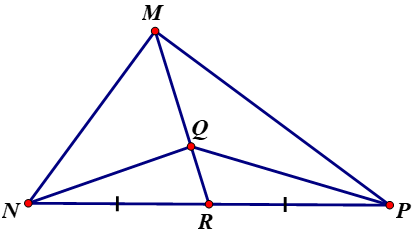
Cho tam giác \(MNP\) với đường trung tuyến \(MR\) và trọng tâm \(Q.\)
a) Tính tỉ số các diện tích của hai tam giác \(MPQ\) và \(RPQ.\)
b) Tính tỉ số các diện tích của hai tam giác \(MNQ\) và \(RNQ.\)
Từ các kết quả trên, hãy chứng minh các tam giác \(QMN, QNP, QPM\) có cùng diện tích.
Gợi ý: Hai tam giác ở mỗi câu a, b, c có chung đường cao.
Phương pháp giải
Áp dụng tính chất trọng tâm của tam giác: Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Hướng dẫn giải
Câu a: Vẽ \(PB \perp MR\) tại \(B\).
Vậy tam giác \(MPQ\) và \(RPQ\) có chung đường cao \(PB.\)
Vì \(Q\) là trọng tâm của \(∆MNP\) nên điểm \(Q\) thuộc đường trung tuyến \(MR\) và \(MQ = 2QR.\)
Ta có: \( S_{\Delta MPQ}= \dfrac{1}{2}MQ.PB\)\(\,= \dfrac{1}{2}. 2QR.PB =QR.PB \)
và \(S_{\Delta RPQ}= \dfrac{1}{2}QR.PB \)
Vậy: \(\dfrac{S_{\Delta MPQ}}{S_{\Delta RPQ}} = \dfrac{QR.PB}{\dfrac{1}{2}QR.PB} = 2 \) (1)
Câu b: Vẽ \(NA \perp MR\) tại \(A\)
Vậy tam giác \(MNQ\) và \(RNQ\) có chung đường cao \(NA.\)
Vì \(Q\) là trọng tâm của \(∆MNP\) nên điểm \(Q\) thuộc đường trung tuyến \(MR\) và \(MQ = 2QR.\)
Ta có: \( S_{\Delta MNQ}= \dfrac{1}{2}MQ.NA\)\(= \dfrac{1}{2}. 2QR.NA =QR.NA \)
và \(S_{\Delta RNQ}= \dfrac{1}{2}QR.NA \)
Vậy: \(\dfrac{S_{\Delta MNQ}}{S_{\Delta RNQ}} = \dfrac{QR.NA}{\dfrac{1}{2}QR.NA} = 2 \) (2)
Câu c: Hai tam giác \(∆RPQ\) và \(∆RQN\) có chung đường cao kẻ từ \(Q\) và \(PR = RN\) nên \({S_{RPQ}} = {S_{RQN}}\)
Vì \({S_{RPQ}} + {S_{RQN}} = {S_{QNP}}\)
Nên \({S_{QNP}} = 2{S_{RPQ}} = 2{S_{RQN}}\) hay \(\dfrac{S_{\Delta QNP}}{S_{\Delta RPQ}} =2\) (3)
Từ (1), (2), (3) ta có: \({S_{MNQ}} ={S_{QNP}} ={S_{MPQ}}\)
(Chú ý: \(S\) là diện tích, ví dụ \({S_{MNQ}}\) là diện tích tam giác \(MNQ\)).
6. Giải bài 68 trang 88 SGK Toán 7
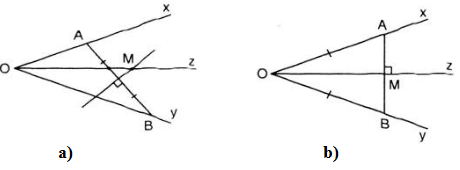
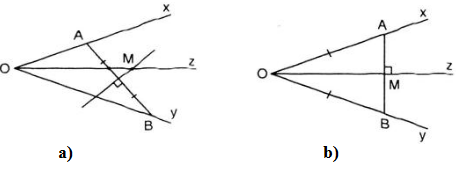
Cho góc \(xOy.\) Hai điểm \(A, B\) lần lượt nằm trên hai cạnh \(Ox, Oy.\)
a) Hãy tìm điểm \(M\) cách đều hai cạnh của góc \(xOy\) và cách đều hai điểm \(A, B.\)
b) Nếu \(OA = OB\) thì có bao nhiêu điểm \(M\) thỏa mãn các điều kiện trong câu a?
Phương pháp giải
- Áp dụng tính chất tia phân giác của góc: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
- Áp dụng tính chất đường trung trực của đoạn thẳng: Điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng.
Hướng dẫn giải
Câu a:
Vì \(M\) cách đều hai cạnh \(Ox, Oy\) của \(\widehat {xOy}\) nên \(M\) nằm trên tia phân giác \(Oz\) của \(\widehat {xOy}\).
Vì \(M\) cách đều hai điểm \(A\) và \(B\) nên \(M\) thuộc đường trung trực của \(AB.\)
Vậy \(M\) là giao điểm của tia phân giác \(Oz\) và đường trung trực của đoạn thẳng \(AB.\)
Câu b:
Nếu \(OA = OB\) thì \(∆AOB\) cân tại \(O\) nên tia phân giác \(\widehat {xOy}\) cũng là trung trực của \(AB\) nên mọi điểm trên tia phân giác \(\widehat {xOy}\) sẽ cách đều hai cạnh \(Ox, Oy\) và cách đều hai điểm \(A\) và \(B.\)
Vậy khi \(OA = OB\) thì có vô số điểm trên tia phân giác \(\widehat {xOy}\) thỏa mãn các điều kiện ở câu a.
7. Giải bài 69 trang 88 SGK Toán 7
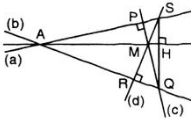
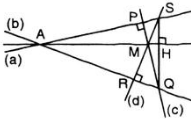
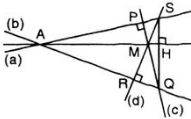
Cho hai đường thẳng phân biệt không song song \(a\) và \(b\), điểm \(M\) nằm bên trong hai đường thẳng này. Qua \(M\) lần lượt vẽ đường thẳng \(c\) vuông góc với \(a\) tại \(P\), cắt \(b\) tại \(Q\) và đường thẳng \(d\) vuông góc với \(b\) tại \(R,\) cắt \(a\) tại \(S.\) Chứng minh rằng đường thẳng qua \(M,\) vuông góc với \(SQ\) cũng đi qua giao điểm của \(a\) và \(b.\)
Phương pháp giải
Áp dụng tính chất ba đường cao của tam giác: Ba đường cao của một tam giác cùng đồng quy tạo một điểm. Điểm đó được gọi là trực tâm của tam giác.
Hướng dẫn giải
Vì \(a\) và \(b\) không song song nên giả sử chúng cắt nhau tại \(A.\)
Xét \(ΔAQS\) có:
\(QP ⊥ AS\) (vì \(QP ⊥ a\)) nên \(QP\) là đường cao của tam giác \(AQS\)
\(SR ⊥ AQ\) (vì \(SR ⊥ b\)) nên \(SR\) là đường cao của tam giác \(AQS\)
Ta có \(QP\) và \(RS\) cắt nhau tại \(M.\) Vậy \(M\) là trực tâm của \(ΔAQS.\)
\( \Rightarrow\) Đường thẳng đi qua \(M\) và vuông góc với \(QS\) tại \(H\) sẽ là đường cao thứ ba của \(ΔAQS.\)
Vậy \(MH\) phải đi qua đỉnh \(A\) của \(ΔAQS\) hay đường thẳng vuông góc với \(QS\) đi qua giao điểm của \(a\) và \(b\) (điều phải chứng minh).
8. Giải bài 70 trang 88 SGK Toán 7
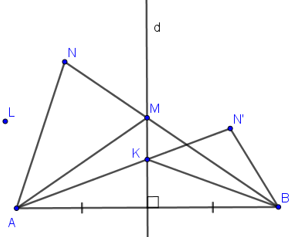
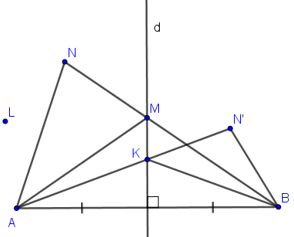
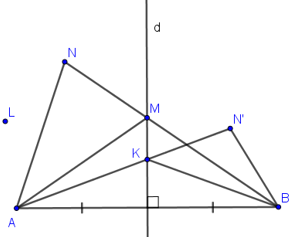
Cho \(A, B\) là hai điểm phân biệt và \(d\) là đường trung trực của đoạn thẳng \(AB.\)
a) Ta kí hiệu \({P_A}\) là nửa mặt phẳng bờ \(d\) có chứa điểm \(A\) (không kể đường thẳng \(d\)). Gọi \(N\) là một điểm của \({P_A}\) và \(M\) là giao điểm của đường thẳng \(NB\) và \(d.\) Hãy so sánh \(NB\) với \(NM + MA;\) từ đó suy ra \(NA < NB.\)
b) Ta kí hiệu \({P_B}\) là nửa mặt phẳng bờ \(d\) có chứa điểm \(B\) (không kể \(d\)). Gọi \(N’\) là một điểm của \({P_B}.\) Chứng minh rằng \(N’B < N’A.\)
c) Gọi \(L\) là một điểm sao cho \(LA < LB.\) Hỏi điểm \(L\) nằm ở đâu, trong \({P_A},{P_B}\) hay trên \(d\)?
Phương pháp giải
- Áp dụng tính chất đường trung trực của đoạn thẳng: Điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó và ngược lại, điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
- Áp dụng bất đẳng thức trong tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì luôn lớn hơn cạnh còn lại.
Hướng dẫn giải
Câu a:
- Ta có \(M\) nằm trên đường trung trực của \(AB\) nên \(MA = MB.\)
Vì \(M\) nằm giữa đoạn \(NB\) nên:
\(NB = NM + MB\) hay \(NB = NM + MA\) (vì \(MB = MA\))
Vậy \(NB = NM + MA\)
- Trong \(ΔNMA\) có: \(NA < NM + MA\) (bất đẳng thức tam giác).
Vì \(NM + MA = NB\) nên \(NA < NB\) (điều phải chứng minh).
Câu b:
Nối \(N'A\) cắt \((d)\) tại \(P.\) Vì \(P\) nằm trên đường trung trực của đoạn \(AB\) nên: \(PA = PB\)
Ta có: \(N'A = N'P + PA = N'P + PB\)
Trong \(ΔN'PB\) ta có: \(N'B < N'P + PB\)
Do đó: \(N'B < N'A\) (điều phải chứng minh)
Câu c:
- Vì \(LA < LB\) nên \(L\) không thuộc đường trung trực \(d.\)
- Từ câu b) ta suy ra với điểm \(N'\) bất kì thuộc \(PB\) thì ta có \(N'B < N'A.\) Do đó, để \(LA < LB\) thì \(L\) không thuộc \(P_B.\)
- Từ câu a) ta suy ra với điểm \(N\) bất kì thuộc \(PA\) thì ta có \(NA < NB.\) Do đó, để \(LA < LB\) thì \(L\) thuộc \(P_A.\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- doc Giải bài tập SGK Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- doc Giải bài tập SGK Toán 7 Bài 3: Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- doc Giải bài tập SGK Toán 7 Bài 4: Tính chất ba đường trung tuyến của tam giác
- doc Giải bài tập SGK Toán 7 Bài 5: Tính chất tia phân giác của một góc
- doc Giải bài tập SGK Toán 7 Bài 6: Tính chất ba đường phân giác của tam giác
- doc Giải bài tập SGK Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng
- doc Giải bài tập SGK Toán 7 Bài 8: Tính chất đường trung trực của tam giác
- doc Giải bài tập SGK Toán 7 Bài 9: Tính chất ba đường cao của tam giác