Giải bài tập SGK Vật lý 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp Fre-nen
Hướng dẫn Giải bài tập Vật lý 12 bài 5 dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải bài tập về tổng hợp hai dao động điều hòa cùng phương, cùng tần số, phương pháp Fre-nen và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 1 trang 25 SGK Vật lý 12
Nêu cách biểu diễn một dao động điều hòa bằng một vecto quay.
Phương pháp giải
-
Vẽ trục tọa độ Ox nằm ngang.
-
Vẽ vecto O.
-
Khi t = 0 ,cho vecto OM quay đều quanh O với tốc độ góc ω.
- Vecto quay OM biểu diễn dao động điều hòa.
Hướng dẫn giải
- Mỗi dao động điều hòa x = Acos(ωt + φ) được biểu diễn bằng một vecto quay. Vecto quay có đặc điểm:
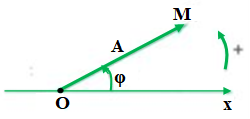
- Có gốc tại gốc tọa độ của trục Ox, có độ dài bằng biên độ dao động A và hợp với trục Ox một góc bằng pha ban đầu φ (chọn chiều dương là chiều của đường tròn lượng giác)
+ Các bước thực hiện:
-
Vẽ trục tọa độ Ox nằm ngang
-
Vẽ vecto \(\overrightarrow {OM} \)
-
Khi t = 0 ,cho vecto \(\overrightarrow {OM} \) quay đều quanh O với tốc độ góc ω.
-
Khi đó, vecto quay OM biểu diễn dao động điều hòa có phương trình \(x = A\cos (\omega t + \varphi )\)
2. Giải bài 2 trang 25 SGK Vật lý 12
Trình bày phương pháp giản đồ Fre-nen để tìm dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số.
Phương pháp giải
-
Lần lượt vẽ hai vecto quay biểu diễn hai phương trình dao động thành phần.
-
Sau đó vẽ tổng hai vecto trên.
-
Vecto tổng là vecto quay biểu diễn phương trình của dao động tổng hợp.
Hướng dẫn giải
Phương pháp giản đồ Fre-nen:
-
Lần lượt vẽ hai vectơ quay biểu diễn hai phương trình dao động thành phần.
-
Sau đó vẽ tổng hai vectơ trên.
⇒ Vectơ tổng là vectơ quay biểu diễn phương trình của dao động tổng hợp.
Cụ thể:
-
Xét 2 dao động cùng phương, cùng tần số:
\(\left\{\begin{matrix} x_1 = A_1 \cos (\omega t + \varphi _1)\\ x_2 = A_2 \cos (\omega t + \varphi _2) \end{matrix}\right.\)
-
Dao động tổng hợp
\(x =x_1 + x_2 = A \cos (\omega t + \varphi )\)
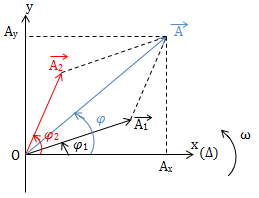
\(\Rightarrow \overrightarrow{A} = \overrightarrow{A_1} + \overrightarrow{A_2}\ (*)\)
-
Chiếu (*) lên: \(\left\{\begin{matrix} Ox: A_x = A_{1x} + A_{2x} \\ Oy: A_y = A_{1y} + A_{2y} \end{matrix}\right.\)
-
Với \(A_x = A\cos \varphi ;\ Ay = A\sin \varphi\)
\(\Rightarrow \left\{\begin{matrix} A\cos \varphi = A_1 \cos \varphi _1 + A_2 \cos \varphi _2\\ A\sin \varphi = A_1 \sin \varphi _1 + A_2 \sin \varphi _2 \end{matrix}\right.\)
\(\Rightarrow A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2A_1A_2\cos (\varphi _2 - \varphi _1)}\)
\(\Rightarrow \tan \varphi = \frac{A_1 \sin \varphi _1 + A_2 \sin \varphi _2}{A_1 \cos \varphi _1 + A_2 \cos \varphi _2}\)
3. Giải bài 3 trang 25 SGK Vật lý 12
Nêu ảnh hưởng của độ lệch pha \({\varphi _2} - {\varphi _1}\) đến biên độ của dao động tổng hợp trong các trường hợp:
a) Hai dao động thành phần cùng pha
b) Hai dao động thành phần ngược nhau
c) Hai dao động thành phần có pha vuông góc
\({\varphi _2} - {\varphi _1} = \pm \frac{\pi }{2} + n\pi \)
Phương pháp giải
Thay các họ nghiệm của \(\Delta \varphi \) với các trường hợp cùng pha, ngược pha và vuông pha vào công thức xác định biên độ của dao động tổng hợp \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _2} - {\varphi _1})} \) . Tìm ra giá trị A.
Hướng dẫn giải
a) Hai dao động thành phần cùng pha: biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: A = A1 + A2
\(\ \Delta \varphi = \varphi _2 - \varphi _1 = k2 \pi\) \(\Rightarrow \left\{\begin{matrix} A = A_1 + A_2\\ \varphi = \varphi _1 = \varphi _2 \end{matrix}\right.\)
b) Hai dao động thành phần ngược pha: biên độ dao động tổng hợp là nhỏ nhất và bằng giá trị tuyệt đối của hiệu hai biên độ: A = |A1 - A2|
\(\ \Delta \varphi = \varphi _2 - \varphi _1 = (2k + 1) \pi\) \(\Rightarrow \left\{\begin{matrix} A = |A_1 - A_2| \ \ \ \ \ \ \ \ \\ \varphi = \varphi _1 \ neu\ A_1 > A_2 \end{matrix}\right.\)
c) Hai dao động có thành phần có pha vuông góc: \(A = \sqrt{(A_1^2 + A_2^2)}\)
\(\ \Delta \varphi = (2k + 1) \frac{\pi}{2} \Rightarrow A = \sqrt{A_{1}^{2} + A_{2}^{2}}\)
4. Giải bài 4 trang 25 SGK Vật lý 12
Chọn đáp án đúng.
Hai dao động là ngược chiều khi:
A. \(\varphi _2 - \varphi _1 = 2n \pi\).
B. \(\varphi _2 - \varphi _1 = n \pi\).
C. \(\varphi _2 - \varphi _1 = (n - 1) \pi\).
D. \(\varphi _2 - \varphi _1 = (2n - 1) \pi.\)
Phương pháp giải
Để chọn phương án đúng ta cần nắm được đặc điểm độ lệch pha của hai dao động ngược chiều.
Hướng dẫn giải
Hai dao động ngược chiều khi độ lệch pha bằng số lẻ lần \(\pi \)
Xét các phương án:
+ Phương án A: \({\varphi _2} - {\varphi _1} = 2n\pi .\) Độ lệch pha của hai dao động bằng số chẵn của π => Hai dao động cùng pha
+ Phương án B: \({\varphi _2} - {\varphi _1} = n\pi\)
+ Phương án C: n-1 cũng có thể chẵn hoặc lẻ => Hai dao động có thể cùng hoặc ngược pha nhau
+ Phương án D: 2n -1 là 1 số lẻ => Thỏa mãn điều kiện ngược pha của hai dao động
⇒ Chọn đáp án D
5. Giải bài 5 trang 25 SGK Vật lý 12
Xét một vectơ quay \(\overrightarrow {OM} \) có những đặc điểm sau:
- Có độ lớn bằng hai đơn vị chiều dài.
- Quay quanh O với tốc độ góc 1 rad/s.
- Tại thời điểm t = 0, vectơ \(\overrightarrow {OM} \) hợp với trục Ox một góc 300.
Hỏi vec tơ quay \(\overrightarrow {OM} \) biểu diễn phương trình của dao động điều hòa nào?
A. \(x = 2cos(t -\frac{\pi}{3} )\).
B. \(x = 2cos(t +\frac{\pi }{6})\)
C. \(x = 2cos(t - 300)\).
D. \(x = 2cos(t + \frac{\pi }{3})\).
Phương pháp giải
-
Viết hương trình tổng quát.
-
Thay các giá trị biên độ, tần số góc và pha ban đầu vào phương trình.
Hướng dẫn giải
Phương trình tổng quát: \(x = A\cos (\omega t + \varphi )\)
Theo đề bài ta có:
-
Có độ lớn bằng hai đơn vị chiều dài ⇒ Biên độ: A = 2 đơn vị chiều dài.
-
Quay quanh O với tốc độ góc 1 rad/s ⇒ Tần số góc: ω = 1rad/s.
-
Pha ban đầu: \(\varphi = {30^ \circ } = \frac{\pi }{6}\)
Vậy, vec tơ quay \(\overrightarrow {OM} \) biểu diễn phương trình của dao động điều hòa : \(x = 2cos(t +\frac{\pi }{6})\)
⇒ Chọn đáp án B
6. Giải bài 6 trang 25 SGK Vật lý 12
Cho hai dao động điều hòa cùng phương, cùng tần số góc \(\omega = 5\pi rad/s\), với các biên độ:
\(A_1 = \frac{\sqrt{3}}{2} cm, A_2 = \sqrt{3} cm\) và các pha ban đầu tương ứng \(\varphi _1=\frac{\pi }{2}\) và \(\varphi _2=\frac{5\pi }{6}.\)
Tìm phương trình dao động tổng hợp của hai dao động trên.
Phương pháp giải
Đây là dạng toán tìm phương trình dao động tổng hợp của hai dao động cho trước, đề bài cho ta các dữ kiện cần thiết là tần số góc \(\omega = 5\pi rad/s\), biên độ và pha ban đầu của 2 dao động.
Cách giải :
- Ta tiến hành giải theo các bước như sau:
-
Bước 1: Tìm Biên độ của dao động tổng hợp theo công thức:
-
\(A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2A_1A_2\cos (\varphi _2 - \varphi _1)}\)
-
Bước 2: Tính \(\varphi\) từ tan\(\varphi\), trong đó: \(\tan \varphi = \frac{A_1 \sin \varphi _1 + A_2 \sin \varphi _2}{A_1 \cos \varphi _1 + A_2 \cos \varphi _2}\) \(\Rightarrow \varphi\)
-
Bước 3: Sau khi có A và \(\varphi\), viết lại phương trình dao động tổng hợp dưới dạng : \(x = A\cos (\omega t + \varphi )\),
Trong đó : \(\omega = 5\pi rad/s\) vì hai dao động điều hòa cùng phương, cùng tần số góc.
Hướng dẫn giải
Áp dụng công thức tính biên độ dao động tổng hợp:
\(\begin{array}{l} {A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _2} - {\varphi _1})\\ \Rightarrow {A^2} = {\left( {\frac{{\sqrt 3 }}{2}} \right)^2} + {\left( {\sqrt 3 } \right)^2} + 2\frac{{\sqrt 3 }}{2}.\sqrt 3 .cos\left( {\frac{{5\pi }}{6} - \frac{\pi }{2}} \right) = \frac{{21}}{4}\\ \Rightarrow A = \sqrt {\frac{{21}}{4}} = 2,3cm \end{array}\)
Pha ban đầu của dao động tổng hợp:
\(\begin{array}{l} tan\varphi = \frac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}\cos {\varphi _1} + {A_2}cos{\varphi _2}}}\\ \Rightarrow tan\varphi = \frac{{\frac{{\sqrt 3 }}{2}\sin \left( {\frac{\pi }{2}} \right){\mkern 1mu} + \sqrt 3 \sin \left( {\frac{{5\pi }}{6}} \right)}}{{\frac{{\sqrt 3 }}{2}\cos \left( {\frac{\pi }{2}} \right){\mkern 1mu} + \sqrt 3 \cos \left( {\frac{{5\pi }}{6}} \right)}}\\ \Rightarrow \varphi = 0,73\pi \end{array}\)
Viết phương trình dao động tổng hợp:
Ta có:
\(\begin{array}{l} \omega = 5\pi \,rad/s\\ A = 2,3cm\\ \varphi = 0,73\pi \end{array}\)
⇒ Phương trình dao động tổng hợp là:\(x = 2,3cos(5\pi t + 0,73\pi )(cm)\)
Tham khảo thêm
- doc Giải bài tập SGK Vật lý 12 Bài 1: Dao động điều hòa
- doc Giải bài tập SGK Vật lý 12 Bài 2: Con lắc lò xo
- doc Giải bài tập SGK Vật lý 12 Bài 3: Con lắc đơn
- doc Giải bài tập SGK Vật lý 12 Bài 4: Dao động tắt dần và dao động cưỡng bức
- doc Giải bài tập SGK Vật lý 12 Bài 6: TH: KS thực nghiệm các ĐL dao động của con lắc đơn



